独立运行微电网平抑有功差额波动研究

石磊，伍阳，刘皓明

(1.国电南瑞科技股份有限公司，江苏南京210061；2.河海大学能源与电气学院，江苏南京210098)

随着传统能源供应的日益紧张以及用电需求的不断提高，人们对可就地消纳可再生能源发电、自治、稳定的微电网的广泛应用变得更加期待[1，2]。目前，微电网的技术发展已经比较成熟，但仍存在很多问题有待解决。微电网运行分为并网运行和独立运行2种模式。对于独立运行的微电网，由于分布式发电，如风力发电、光伏发电，受自然因素的影响，其输出功率具有间歇性、随机性和波动性[3]，以及负荷峰谷差特性，一天中的有功功率差额存在较大的波动性[4]，不利于后备电源的稳定经济运行。对此，许多学者提出了通过投切负荷和调度后备电源出力的方法平抑有功功率差额波动。文献[5]和[6]提出了投切负荷的方法，以减小微电网有功功率缺额，该方法虽然能有效减小微电网有功功率的差额，但由于有功差额存在明显的波动，频繁地投切负荷，既不能保证负荷用电的可靠性，也不利于微电网的稳定。文献[7]提出了采用燃料电池作为后备电源，由于有功差额的波动性，需要频繁地对后备电源进行调度，必然对后备电源性能要求很高，且控制复杂，还不经济。本文以独立运行的微电网为研究对象，采用储能装置平抑微电网有功功率差额的波动，使系统有功差额在很小范围内变化，更利于后备电源稳定经济运行。建立独立运行微电网有功功率差额最小的数学模型，充分考虑储能装置的荷电状态（SOC）等因素。通过动态规划算法对数学模型求解和算例仿真，验证了数学模型的有效性及动态规划算法应用于平抑独立运行微电网有功差额波动问题的适用性。

1 数学模型

1.1 前提假设

通常将微电网一天的有功功率差额总体情况作为考虑对象，对储能装置的出力调度以5 min为控制周期。光伏发电及风力发电等微电源，一般通过控制使其工作在最大功率输出状态，其输出受自然条件的影响，在该数学模型中，作为已知预测量[8]。储能系统平抑微电网有功差额波动是一个较复杂的优化问题，为使建立模型更合理，作如下假设：

（1）一天内的总负荷需求和微电源的出力曲线已知；

（2）储能装置响应时间远小于控制周期，忽略不计；

（3）同一控制周期内，储能装置处于同一充放电状态；

（4）电力网络损耗在更高一级的控制调度中计及，文中所建模型仅计及储能装置充放电效率和自放电现象。

1.2 目标函数

根据负荷需求和微电源的出力，通过控制储能装置的充放电，以尽可能地平抑微电网有功差额波动为目的建立目标函数，为取得最优解，加入了对不符合条件取值的惩罚[9，10]。系统的数学模型的目标函数可用数学式表示如下：

式中：M为控制周期数，取M=288；PES（i）为第i个控制周期储能装置输出功率；ΔP（i）为第i个控制周期内负荷需求功率与微电源输出有功之差。

式中：PG（i）为第i个控制周期内系统中微电源出力；PL（i）为第i个控制周期内负荷需求；ΔT为控制周期；N为储能系统中储能装置的配置数量；ΔC（i）为单个储能装置第i个控制周期增加电量；Cd（i），Cc（i）分别为单个储能装置在第i控制周期的实际放电和充电电量；uc（i），ud（i）分别为第i个控制周期内储能装置充电和放电的状态标志，满足：

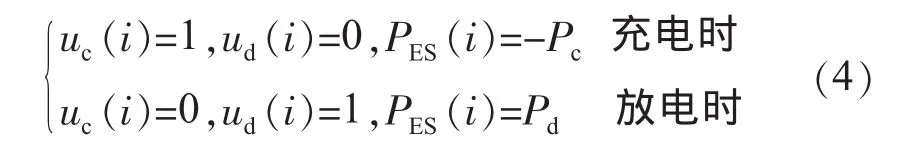
1.3 约束条件

1.3.1 SOC约束

式中：SOCmin，SOCmax分别为储能装置荷电状态最小和最大允许值；SOC（i）为第i个控制周期单个储能装置的荷电状态。

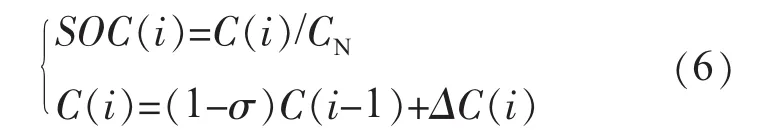
式中：C（i）为第i个控制周期单个储能装置的剩余电量；CN为单个储能装置的额定电量。

1.3.2 充放电约束

式中：Pc，Pd分别为储能装置的额定充电和放电功率；σ为储能装置的自放电率；ηc，ηd分别为储能装置充电和放电效率。

1.3.3 循环控制约束

式中：SOC（0），SOC（M）分别为一天开始和结束时储能装置的荷电状态。

1.4 模型分析

由数学模型可知，采用传统的优化算法进行优化时，目标函数有288个控制变量PES（i），i=｛1，2，……，288｝，控制变量较多，其解的空间很大，难以寻找到最优解，且计算较费时，收敛性差。

实际上，数学模型是一个多阶段非线性规划问题，即属于动态规划的问题。此时的目标函数仅含有1个动态变量，存在多个控制周期内状态变量间耦合的问题，即可将数学模型按动态规划问题求解。采用动态规划算法求解此数学模型，控制变量明显减少，容易求解，效率高，收敛性好，且能获得最优解[11]。

2 模型求解

2.1 动态规划算法

动态规划是研究多阶段决策过程最优解的一种有效方法。

适用动态规划求解问题，必须具备下列特征[12]：（1）问题必须能划分成若干个相互关联的阶段，每个阶段皆具有状态变量，相邻阶段由状态变量联系；（2）每个阶段的某个决策变量能使该阶段某一状态变量转换成下一阶段某一状态变量；（3）每个阶段所做的最佳决策只影响其后的各阶段，而对前一阶段的决策无影响。

由第2节可知，文中建立的数学模型是一个多阶段非线性规划问题。目标函数为求取多个控制周期内储能装置输出有功与微电网有功差额的差值最小化，且约束方程包含前一控制周期的储能装置剩余电量，符合动态规划求解的基本特征。

2.2 转化模型

采用动态规划算法求解模型，必须将模型转化为动态规划可操作的方式，涉及到阶段、状态、决策、策略[12]。

（1）阶段。将1天分为若干阶段（即控制周期），其中任意阶段标记为阶段k，文中k=｛1，2，……，288｝。

（2）状态。将储能装置的充放电动作设为状态。

（3）决策与策略。以储能装置的充放电动作作为状态，那么储能装置每个阶段的充放电电量就是决策，144阶段的不同决策组合就是策略。

（4）状态转移方程。

（5）阶段目标函数。

（6）最终目标函数。

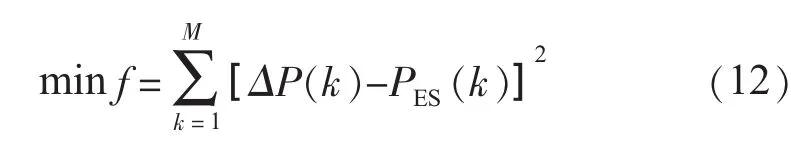
（7）动态规划算法递归方程。

2.3 算法框图

动态规划算法应用于独立微电网系统的主要求解过程分为3步。

第1步，在第k个阶段中，首先在[CNSOCmin，CNSOCmax]范围内取所有可能的Ci（k）；在ΔC（k）∈{ΔC}取值范围内，根据状态的取值，选取所有可能的ΔCj（k）。为了方便计算，状态方程求解过程中采用逆序求解，即根据第k个阶段数据和状态转移方程逆函数求得Cij（k-1），再根据约束条件CNSOCmin≤Cij（k-1）≤CNSOCmax去除不符合条件的Cij（k-1）。

第2步，根据第1步最后得到的Cij（k-1）和与其对应的ΔCj（k）计算目标函数值，对于相同的Cij（k-1），通过比较目标函数，选取储能装置剩余电量最优值。

第3步，判断是否计算完所有的控制周期，若没有，返回到第1步。

根据上面的3个步骤，应用动态规划算法求解的解法框图如图1所示。

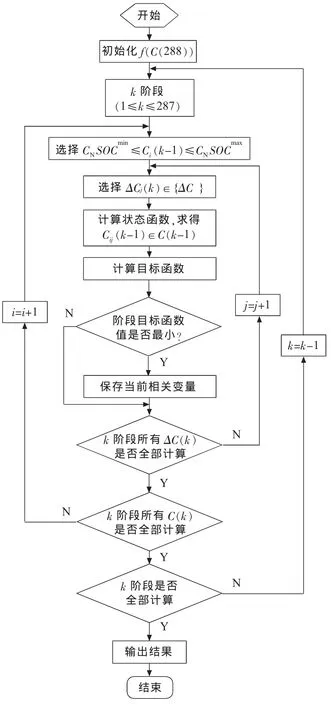
图1 动态规划法的解法框图

3 仿真分析

仿真分析中，独立微电网的负荷有功需求最大值为1100kW，微电源的最大有功输出值为850kW，微电源的输出功率数据和负荷需求曲线如图2所示。储能系统的单个储能装置的规格为：额定充电功率和放电功率均为100kW，额定容量为480kW·h，充放电率均取87%，SOC允许的最大值和最小值分别为20%和100%。

仿真分析中，当储能装置配置数量N=3和N=6时，分别进行了计算，并给出了2种情况下的储能系统平抑有功功率差额的效果图和储能系统的变化仿真波形图，如图3和图4所示。

从图3（a）可知，经过储能装置的合理优化调度，使得系统有功功率差额波动得到有效平抑；但由于储能装置容量配置不足，无法保证一天内有功缺额恒定，同时受最大充放电功率限制，可能存在个别尖峰无法平抑。由图4（a）可知，当储能容量配置合理时，可使得全天系统有功功率缺额恒定，有利于后备电源调度的平稳性，提高了系统运行的经济性。从图3和图4中（b）可知，仿真中，能满足储能的SOC约束和循环控制约束等约束条件。

4 结束语

以储能装置平抑微电网有功功率差额波动为目标，计及储能装置的SOC、充放电效率等因素，建立了数学模型，考虑到不同控制周期内的储能装置剩余电量存在耦合性，采用动态规划算法求解，仿真分析得出如下结论：（1）独立运行的微电网，需要合理配置一定容量的储能装置，以保证系统平稳经济运行；（2）动态规划算法有效地解决了数学模型中状态变量耦合问题，且通过算例仿真，验证了该算法的适用性；（3）储能平抑独立运行微电网有功功率差额的效果与其最大充放电功率和容量有关。

[1] LASSETER R，AKHIL A，MARMAY C，et al．Integration of Distributed Energy Resources:the CERTS Microgrid Concept[EB/OL].http://certs.lbl.gov/pdf/50829.pdf,2007-04-01.

[2] MARNAY C,RUBIO F J,SIDDIQUI A S.Shape of the Microgird[EB/O L].http://escholarship.org/uc/item/9fw029wb,2007-01-01.

[3] TAN H G,WANG B,LIU D C,et al.Analysis of Distributed Generation System Based on Micro-Grid and Its Impaction on Voltage Distribution[C].Asia-Pacific Power and Energy Engineering Conference,2011.

[4] 孙超.独立运行的光伏系统的研究[D].南京：南京航空航天大学硕士学位论文，2009.

[5] LOPES J A P,MOREIRA C L,MADUREIRA A G,et al.Control Strategies for Microgrids Emergency Operation[C].International Conference on Future Power Systems,2005.

[6] CHATZIVASILIADIS S J,HATZIARGYRIOU N D,DIMEAS A L.Development of an Agent Based Intelligent Control System for Microgrids[C].IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century,2008.

[7] NAYAR CV,ASHARI M,KEERTHIPALA W W L.A Gridinteractive Photovoltaic Uninterruptible Power Supply System Using Battery Storage and a Back up Diesel Generator[J].IEEE Transactions on Energy Conversion,2000，15（3）：348-353.

[8] 陈达威，朱桂萍.微电网负荷优化分配[J].电力系统自动化，2010，34（20）：45-49.

[9] 李碧辉，申洪，汤涌，等.风光储联合发电系统储能容量对有功功率的影响及评价指标[J].电网技术，2011，35（4）：123-128.

[10] 丁明，徐宁舟，毕锐.用于平抑可再生能源功率波动的储能电站建模及评价[J].电力系统自动化，2011，35（2）：66-72.

[11] ZHANG L,LI Y Y.Optimal Energy Management of Hybrid Power System with Two-scale Dynamic Programming[C].American Control Conference,2011.

[12] 刘光中.动态规划－理论及其应用[M].成都：成都科技大学出版社，1991.