边界约束对钢筋混凝土异形板受力性能的影响

杨华宝

(太原理工市政设计院(有限公司)，山西 太原 030024)

0 引言

板作为抗侧力水平构件，可保证建筑物的空间整体性能和水平力的有效传递，是结构体系中较为重要的一部分，影响着整个结构的安全性和经济性，同时也是工程界应用最为广泛的一种结构形式。其中，建筑工程中的楼板是各种板结构中应用数量最多、边界约束条件最为复杂的一类板［1］。

对于钢筋混凝土楼盖，最初进行设计时，主要是利用梁将平面布置不规则的板分隔成几块矩形板，这样会造成楼层顶部见梁，不仅影响室内美观，而且影响室内竖向空间的充分利用。为解决上述问题，随之而产生了钢筋混凝土异形板，而且异形板的跨度在不断增大，特别是在钢筋混凝土剪力墙结构中得到了广泛的应用。但在实际工程中，尤其是住宅结构中，楼板的开裂现象比较常见，影响建筑功能的正常使用。由于异形板的受力性能比较复杂，钢筋混凝土异形楼板的出现，使得设计面临新的问题。

1 计算模型的建立

1.1 工程实例

以某剪力墙结构中一块典型的“Z”字形钢筋混凝土异形楼板(板厚h=130 mm)为例，板的混凝土强度等级为C30，该异形板的具体平面尺寸如图1所示。由此可知，板的厚度与短跨之比约为130/(2900+1200)=1/32。

1.2 有限元模型

应用有限元分析软件ANSYS，采用Shell63单元(该单元为四节点弹性壳单元，每个节点具有6个自由度，即X，Y，Z方向的线位移以及转角，可以同时承受壳面内、外的荷载，同时具有壳单元算法和膜单元算法，考虑了应力刚化效应以及大变形效应［2］)，建立该异形板的有限元模型:混凝土弹性模量为3.0×1010N/m2(C30)，泊松比为0.2，钢筋混凝土自重取为25 kN/m2。

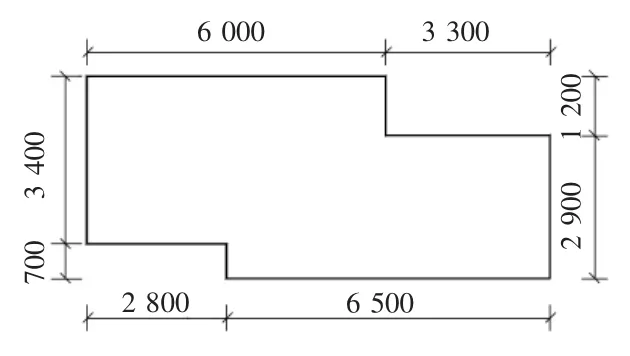
图1 结构平面布置图

在异形板的有限元模型中，划分网格规格为0.1 m×0.1 m，共有3221个Shell63单元，有限元模型见图2。

异形板除自重外，考虑楼板的面层自重，附加恒载以及楼面活载取值如下:

面层自重:2.0 kN/m2;

活载:3.5 kN/m2(依据荷载规范［3］，住宅活载标准值为2.0 kN/m2，考虑非承重墙分摊在板上的荷载);

一是党派活动类。此类主题的优质推文数量最多，共32篇，占25.6%，关键词有五一口号（6）、中国共产党（6）、纪念（5）、公众（4）、投票（4）等。其中13篇线上活动类文章阅读量均较高，这类推文采用投票、抽奖、答题等形式最大化调动党派成员的参与热情。如江苏农工发布的推文《农工党江苏省委纪念中共中央“五一口号”发布70周年征文微信投票》。

恒、活载组合:

1.2×(0.13 × 25+2.0)+1.4 × 3.5=11.2 kN(活载控制时);

1.35×(0.13 ×25+2.0)+0.7 ×1.4 ×3.5=10.5 kN(恒载控制时)。

由此可得，作用在板上荷载的设计值为11.2 kN(取上述两组合值中的较大值)。

图2 异形板的有限元模型

1.3 边界约束的确定

根据实际工程经验，建筑工程中楼板的边界约束主要有以下三种情况:

1)若该异形板的板厚同周边板的厚度相差不大时，或周边的剪力墙厚度较大时(如剪力墙结构中的地下室外墙，墙厚不小于300 mm)，可假定板的周边约束全为嵌固，如图3a)所示;

2)若该异形板的板厚同周边板的厚度相差较大时，或周边的剪力墙厚度较小时(板厚接近墙厚或与墙厚相差不大)，可假定板的周边约束全为简支，如图3b)所示;

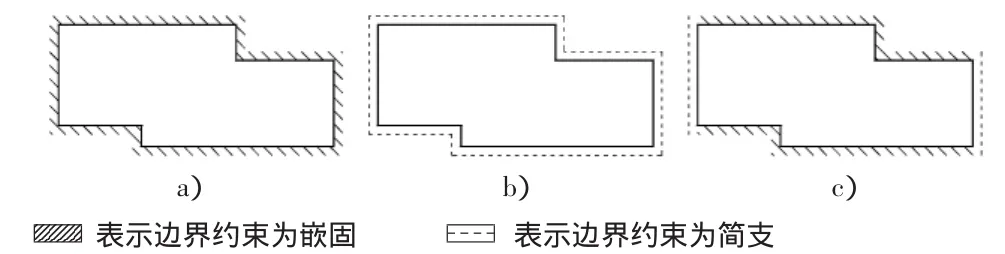
图3 不同边界约束下的异形板

2 结构分析

2.1 薄板理论

薄板假定是较早发展起来的一种板的分析理论，即所谓的基尔霍夫板(G.R.Kirchhoff)，对于一般的钢筋混凝土楼板，在弹性阶段的计算分析均采用该假定。

薄板理论基本假定如下［4］:

1)假定板体材料是均匀、连续的理想弹性体;

2)假定位移和形变都是微小的，薄板的厚度h与最小外形尺寸相比是很小的(h/lmin＜1/5)，而板的最大挠度与厚度相比是微小的(ωmax/h≤1/5)，并且应变与转角都远小于1;

3)假定薄板弯曲时板的中面不发生面内变形，这是刚性板弯曲的属性;

4)直线法假定，变形前垂直于板中面的直线段，在变形后仍为直线段，而且仍是垂直于变形后的中面，直线段长度不变;

5)假定板中面的各平行层间变形中不挤压，即忽略垂直于平板中面的法向应力σz。

2.2 异形板的受力分析

对板输入面荷载设计值11.2 kN(11200 N)，分别对上述三种情况的异形板进行整体变形和等效应力两个方面的静力分析。

2.2.1 整体变形

经计算得出，异形板分别在上述三种不同边界约束下的整体变形变化情况以及产生的最大与最小位移，具体见图4和表1。

表1 异形板的最大与最小位移 mm

异形板在不同的边界约束下，整体变形的变化趋势基本相同，板周边的变形较小、中部的变形较大，整体变形总体上呈“Z”字形，这主要是由板的形状引起的。当板的边界约束全为嵌固时比全为简支时的整体变形影响范围小，当板的边界既有嵌固又有简支时的整体变形范围则介于两者之间。在三种情况下，异形板的最大及最小变形产生部位基本一致。

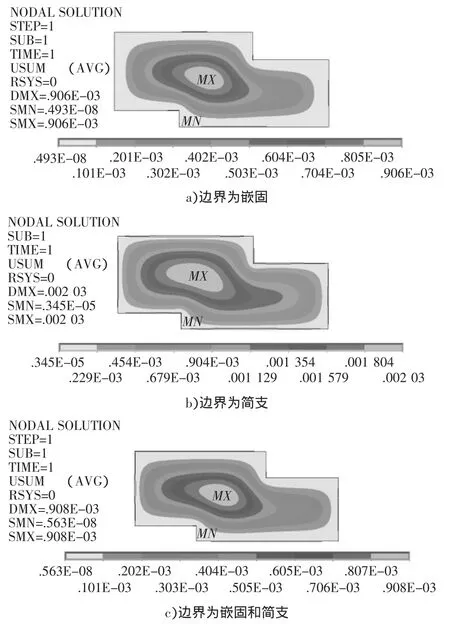
图4 异形板的整体变形

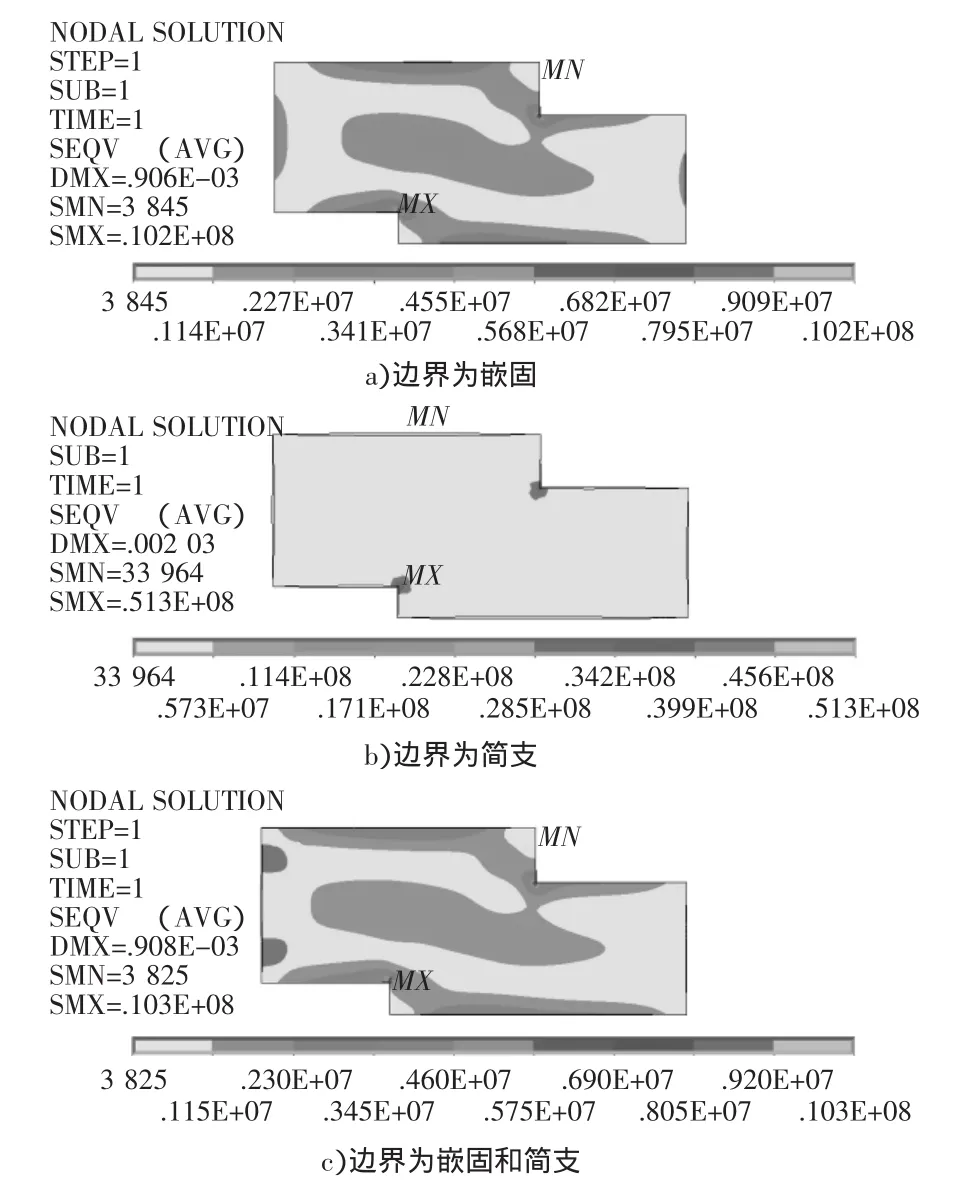
图5 异形板的等效应力

当板的边界约束全为嵌固时产生的最大及最小位移均小于全为简支时的，当板的边界约束既有嵌固又有简支时同样介于两者之间，和板边界约束全为嵌固时接近。之所以边界全为嵌固和边界既有嵌固又有简支两种情况的位移相差不大，是因为后者的长边约束为嵌固，说明长边约束的作用远大于短边的简支约束。

2.2.2 等效应力

经计算得出，异形板分别在上述三种不同边界约束下的等效应力变化情况以及产生的最大与最小等效应力，具体见图5和表2。

异形板在不同的边界约束下，当边界约束为嵌固时的等效应力的变化情况与边界既有嵌固又有简支时基本相同，板内应力分布不均;当边界全为简支时，与上述两种情况相差较大，板内应力分布比较均匀。在三种情况下，均表现出板的凹角处产生应力集中现象。

表2 异形板的最大与最小等效应力 kN

当板的边界约束全为嵌固时与全为简支时相比，边界嵌固时产生的最大等效应力约是简支时的1/5，最小等效应力约是简支时的1/9。当板的边界约束既有嵌固又有简支时与边界全为嵌固时的最大、最小等效应力变化情况基本相同，说明边界既有嵌固又有简支时的长边约束作用远大于短边的简支约束作用。

3 结语

通过分析得出，当异形板的边界全为嵌固时，板的整体变形及等效应力变化幅度均小于边界全为简支时的，而且整体变形的变化规律与边界全为简支时的也基本相同，但等效应力的分布规律却与边界全为简支时不同。当异形板的边界既有嵌固又有简支时，板表现出与边界全为嵌固时基本相同的受力性能，这主要是由于板的长边嵌固约束作用远大于其短边的简支约束作用。

由此可得，边界约束直接影响板的受力性能，鉴于异形板的形状比较复杂，致使其受力性能也比较复杂，确定其合理边界约束显得尤为重要。

［1］张裕媛.带凹角钢筋混凝土板的设计与研究［D］.天津:天津大学，2005:1-2.

［2］尚晓江，邱 峰，赵海峰.ANSYS结构有限元高级分析方法与范例应用［M］.第2版.北京:中国水利水电出版社，2008.

［3］GB 50009-2001，建筑结构荷载规范［S］.

［4］李 鹏.钢筋混凝土板的弹塑性有限元分析［D］.西安:西安建筑科技大学，2008:8-9.