用积分算子定义的强星象函数的子类

华 芳，徐厚生

（镇江高等专科学校 教师教育系，江苏 丹阳 212300）

设A表示在单位圆盘E={z：|z|＜1}内解析，具有形式

的全体函数组成的类，若函数f（z）∈A满足

则称f（z）为γ型β阶强星象函数，记作f（z）∈S*（β，γ），其中0≤γ＜1，0＜β≤1。若函数f（z）∈A满足

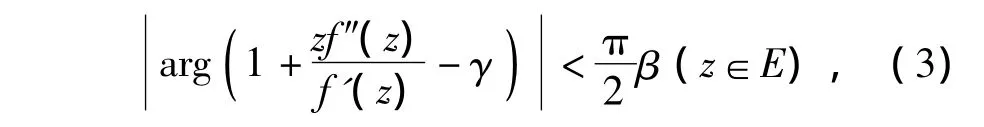
则称f（z）为γ型β阶强凸象函数，记作f（z）∈C（β，γ）。其中0≤γ＜1，0＜β≤1。易知f（z）∈C（β，γ）⇔zf’（z）∈S*（β，γ）。

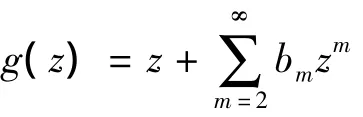
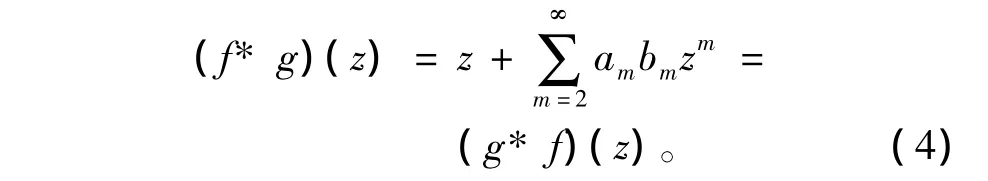
设f（z）∈A，定义A上的积分算子In，

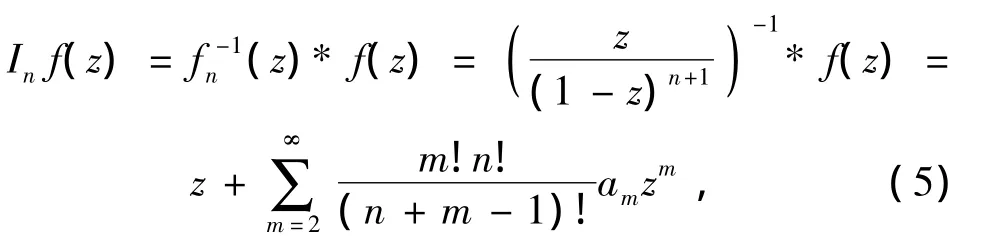
该算子由Liu和Noor在文献［1-5］中首先研究的。可以看出

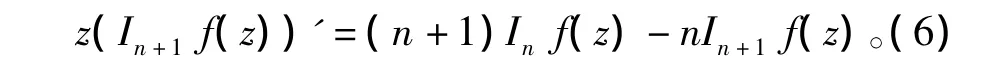
利用算子Inf（z）可以刻划2个新的函数类

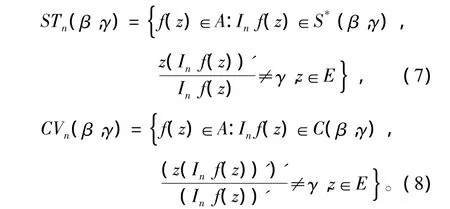
不难看出，f（z）∈CVn（β，γ）⇔zf’（z）∈STn（β，γ）。

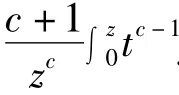
1 引理

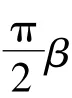
2）p（z0）=（±ia）β（a＞0）。

2 定理1

定理1STn（β，γ）⊂STn+1（β，γ）。

证明 设f（z）∈STn（β，γ），置

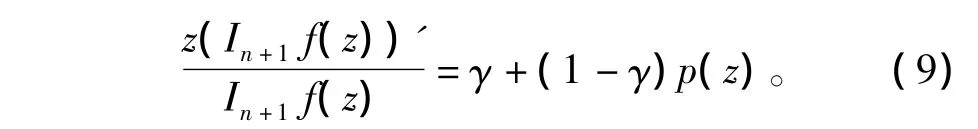
这里p（z）=1+c1z+c2z2+…在E内解析，且p（z）≠0（z∈E）。利用式（6），式（9）可以改写成

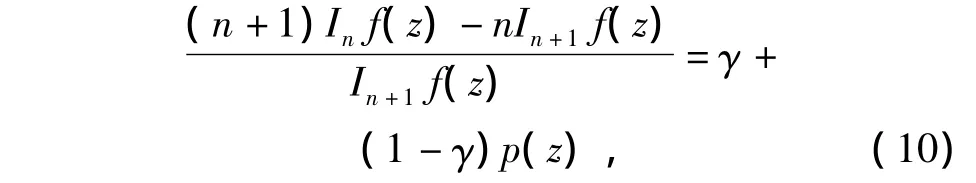
得

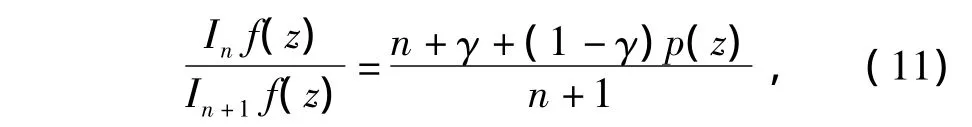
对数微分式（11），再利用式（9）整理得

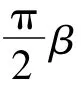
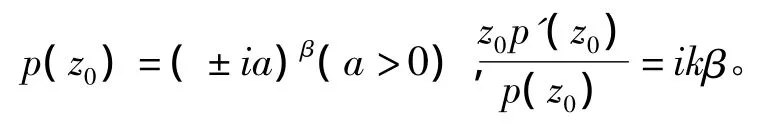
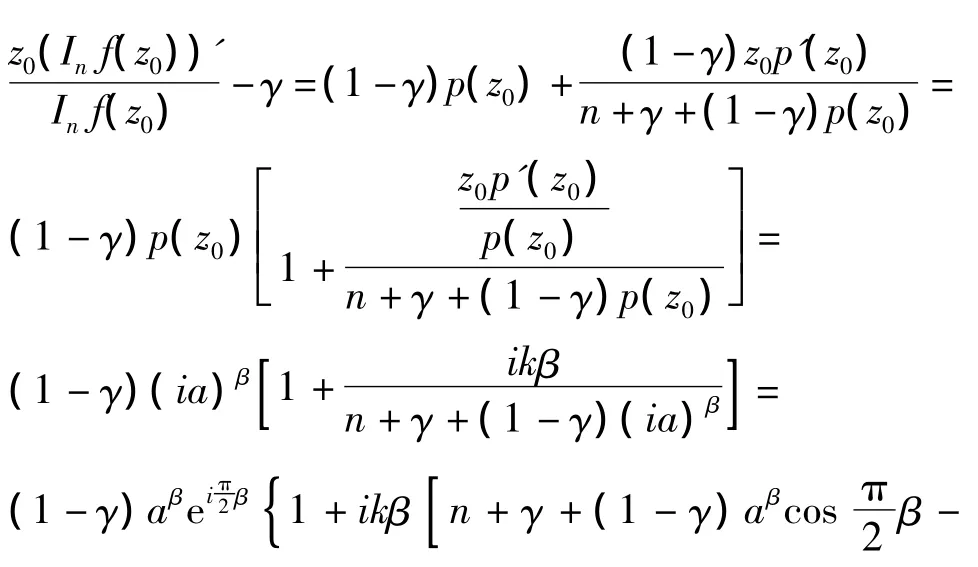
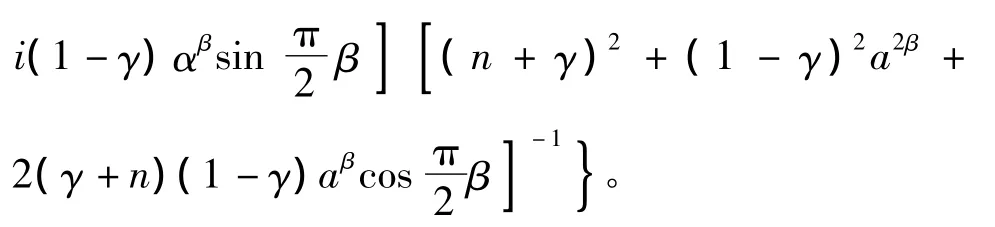
因此，

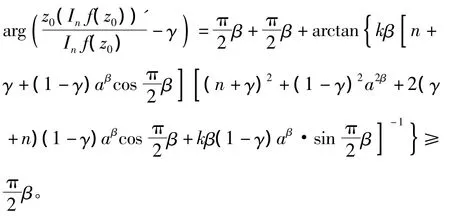
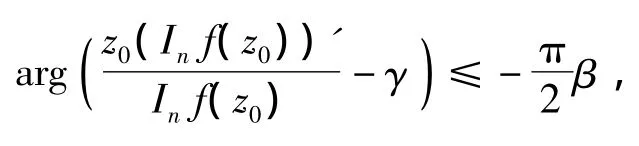
所以，f（z）∈STn+1（β，γ）。

3 定理2

定理2CVn（β，γ）⊂CVn+1（β，γ）。

证明f（z）∈CVn（β，γ）⇔zf’（z）∈STn（β，γ）（由定理1）⇒zf’（z）∈STn+1（β，γ）⇔f（z）∈CVn+1（β，γ）。

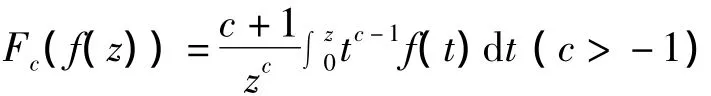
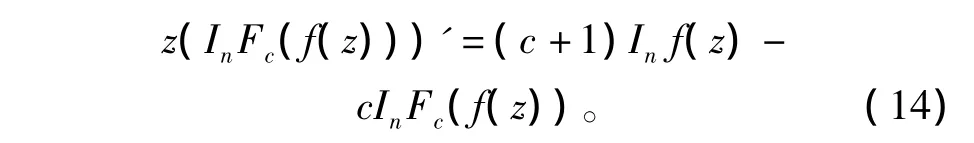
4 定理3

定理3 若c+γ＞0，当f（z）∈STn（β，γ）时，Fc（f（z））∈STn（β，γ）。

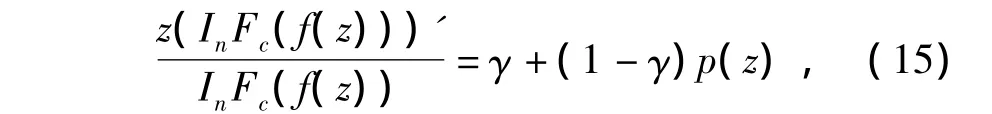
证明 设f（z）∈STn（β，γ），令这里p（z）在E内解析，且p（0）=1，p（z）≠0（z∈E），利用式（14），式（15）可得

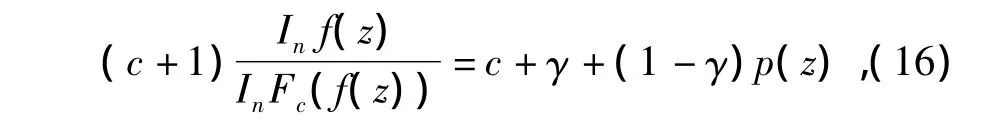
对数微分式（16），并利用式（15）整理得

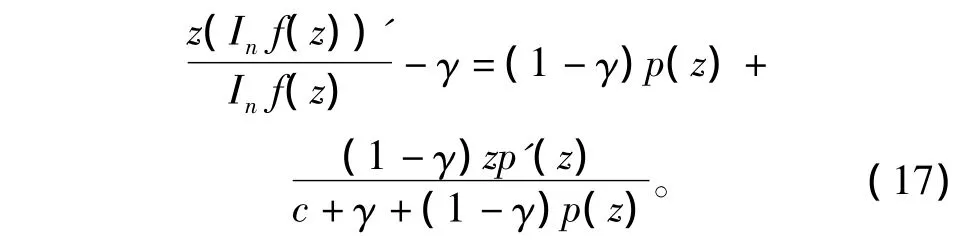
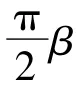
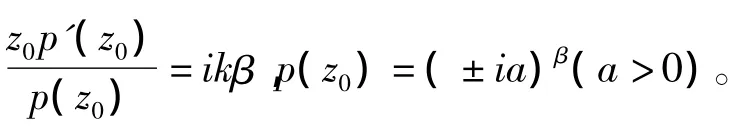
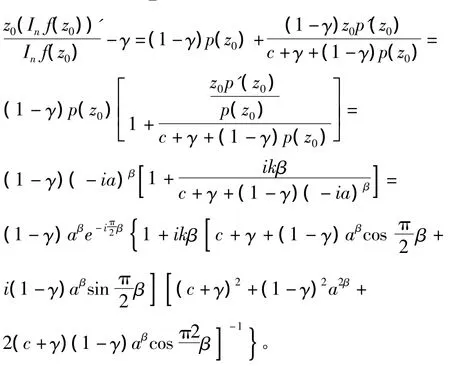
因此，

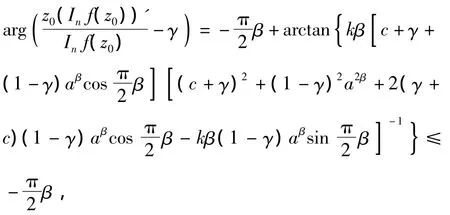
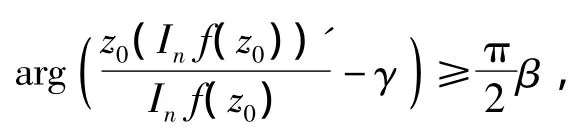
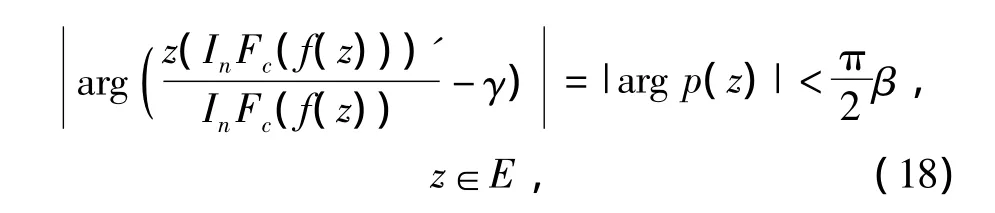
所以，Fc（f（z））∈STn（β，γ）。

5 定理4

定理4 若c+γ＞0，当f（z）∈CVn（β，γ）时，Fc（f（z））∈CVn（β，γ）。

证明 应用定理3和f（z）∈CVn（β，γ）⇔zf’（z）∈STn（β，γ），即得。

［1］NOOR K I.On new classes of integral operators［J］.J.Nat.Geometry，1999（16）：71-80.

［2］NOOR K I，NOOR M A.On integral operators［J］.J.Math.Anal.Appl.，1999（238）：341-352.

［3］LIU J L，NOOR K I.Some properties of Noor integral operator［J］.J.Nat.Geometry，2002（21）：81-90.

［4］LIU J L.Properties of certain subclass of multivalent functions defined by an integral operator［J］.Complex Variables and Elliptic Equations，2009（54）：471-483.

［5］LIU J L.Some properties of certain multivalent analytic functions associated with certain integral operator［J］.Indian J.Math.，2006（48）：259-273.

［6］NUNOKAWA M.On properties of non-caratheodory functions［J］.Proc.Japan Acad.Ser.A Math.Sci.，1992（68）：152-153.