基于物元理论的任意功能树相似扩展方法

刘晓平， 陆劲挺

（合肥工业大学计算机与信息学院可视化与协同计算研究室，安徽 合肥 230009）

基于物元理论的任意功能树相似扩展方法

刘晓平， 陆劲挺

（合肥工业大学计算机与信息学院可视化与协同计算研究室，安徽 合肥 230009）

功能模型是概念设计的核心处理对象，功能树是一种典型的、应用广泛的功能模型。使用现有相似度计算方法计算任意功能树的相似度存在困难。因此，基于布尔代数提出了析取范式树的概念，以及两种求解析取范式树的方法，并描述了任意功能树的物元相似度计算方法。拓展了功能树相似扩展方法的应用范围，扩大了设计解空间，增加了获得创新解的可能性，最后给出实例验证了方法的有效性。

计算机应用；功能树；析取范式树；物元相似度

概念设计是产品设计最具有创造性的阶段，决定了产品从设计到生产所有费用的75%[1]，决定了产品的创新性和市场竞争力。功能模型是概念设计的核心处理对象[2]，目前在概念设计中的功能模型种类繁多，其中功能树是一种典型的、应用极其广泛的功能模型[3-5]。

功能树的建立主要依赖领域专家的专业知识水平，然而仅凭借人的思维难以将问题考虑全面，所以专家所建的功能树往往蕴含的信息不完备，因而，需要计算机辅助进行功能树的扩展，使设计信息尽可能的完备，避免遗失重要的设计解。

现有相似度计算方法难以直接计算结构复杂的功能树之间的相似度，因此需要一套通用的、能够对任意功能树进行比较的相似度计算方法，而后再进行相似扩展。文献[6]提出了基于人类相似联想的相似扩展方法的基本思想。基于这种思想笔者在文献[7]提出了一种有约束的功能树对比相似度计算方法，以及对比相似扩展的具体方法。但是任意功能树的相似度计算方法鲜有提及。

由于功能树的功能函数是布尔表达式，所以结合布尔代数的规则，提出了析取范式树的概念，并给出两种求解析取范式树的算法，最后描述了任意功能树的相似度计算方法。拓展了功能树相似扩展方法的应用范围，扩大了设计解空间，增加了获得创新解的可能性。

1 背 景

产品概念设计中，功能树的建立需要先确定总功能，而后采用自顶向下的方法分解总功能，再将其子功能作为总功能进行分解，直到分解得到的子功能为不能再分的基本功能。总功能节点和子功能节点统称为功能节点，其关系可通过“与”、“或”、“非”3种门节点进行表示，而不可再分的叶子节点为基本功能节点，否则为可扩展功能节点。

定义1 基本功能变量 假设设计需求S最终可分解为n个基本功能，则定义基本功能变量xi为一个布尔变量，其中，

对设计需求的求解，本质上即是对功能树顶功能实现方案的求解，顶功能变量的值是由基本功能变量决定的。

定义 2 功能函数 对于 n维向量X = (x1,x2,…, xn)，其中任一分量xi为基本功能变量，称布尔函数 φ( X ) = φ(x1,x2,… ,xn)为n维向量X上的功能函数，简称功能函数，存在

功能函数本质上是把功能树和布尔代数运算规则映射起来的纽带，任意一棵含“与”、“或”、“非”门的功能树都存在对应的功能函数，其计算依照布尔代数运算规则。

2 析取范式树求解

2.1 任意功能树相似度的计算障碍

相似理论[8]中的相似度计算方法在涵义上并未考虑“或”和“非”两种系统要素组成的方式，因此，当试图计算与或非功能树之间的相似度时，发现简单地套用基于相似理论的功能树相似度计算方法[7]进行计算是不可行的，其存在的问题主要有以下3点：

1） 若两棵功能树的层高不同，则不满足相似度计算的初始条件；

2） 若两棵树的门类型分布不同，即使层高相同，两树表达的实际意义也不同，因而直接计算存在意义偏差；

3） 若根据布尔代数运算法则整理两树的门类型，试图使其保持一致，又由于与门、或门、非门 3种门类型的排列组合情况与功能树的规模、节点排列方式等因素密切相关，则有可能导致复杂问题求解。

上述 3种情况是影响功能树计算的主要因素，可见现有功能树相似度计算方法不能有效解决任意两棵功能树的相似度计算问题。

2.2 析取范式树的定义

定理1 设 E(x1,x2,… ,xn)是布尔代数＜ A,∨,∧,¬＞上的任意一个布尔表达式，则它一定存在析取范式[9]。

由于功能函数φ ( X)是布尔表达式，则一棵功能树所对应的 φ( X)必存在析取范式形式φd(X )，即化为积之和的形式，即其中 Di为表达式中第i个布尔积项，对应一个功能集δi，m为表达式中布尔积项的个数，并且Fi= {j|xjin Di}，(¬) xj表示叶子节点 xj的门类型可能为非门。

同理，已知布尔函数φ ( X)，也可以画出其所对应的功能树。当φ ( X)化为析取范式形式之后，其对应的功能树结构也相应发生变化。

定义3 析取范式树 功能树T存在功能函数φ ( X)，功能函数φ( X)存在析取范式φd(X)，φd(X )是功能树 Td的功能函数，则称任意功能树 Td都是功能树T的析取范式树。

由于功能函数 φ( X)的析取范式φd(X)可能是不唯一的，所以功能树T的析取范式树 Td也可能是不唯一的。析取范式树的形态和功能树的初始形态、叶子节点的规定排序以及析取范式树求解的过程等因素相关。由布尔定律知，φ( X)与φd(X )存在相同的真值表，因此，功能树T与其析取范式树 Td存在相同的解空间，可认为功能树T等价于其析取范式树 Td。

已知 φ( X)的析取范式φd(X)为积之和的形式，如果φd(X)只含有一个布尔积项，析取范式树 Td是一棵根节点为与门的两层功能树，如图1所示。如果φd(X )含有多个布尔积项，则析取范式树 Td可能是一棵根节点为或门的两层功能树，如图2所示。或者是只有根节点为或门的3层功能树，如图3所示。

图1 两层析取范式树示例一

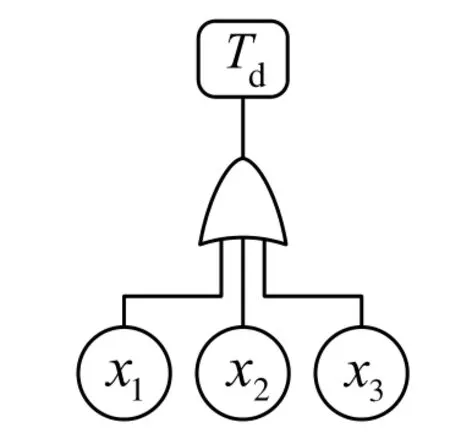
图2 两层析取范式树示例二

当任意功能树转化为析取范式树后，其析取范式树的每个布尔积项都对应顶功能的一个解，从而可以通过比较布尔积项之间的相似程度来衡量功能树之间的相似度，使得任意功能树的相似度计算成为可能。

图3 三层析取范式树示例

将布尔函数化为析取范式形式常用的方法有真值法和公式化归法[9]。真值法中，每个布尔变量可取0或1两个值，若有n个布尔变量，则真值表有2n行，当布尔变量数量增加时，真值表的容量呈指数级增长，容易导致NP问题。公式化归法在布尔代数运算法则的指导下从词法的角度对布尔函数进行变换，是一种普遍使用的求解析取范式的方法。下面介绍两种基于公式化归法求解析取范式树的具体算法。

2.3 门类型解析法

门类型解析法通过对节点门类型的判断，对结构化的功能树的节点直接进行相应的修改和增删操作，通过依次执行“非门下降”、“或门提升”、“与门合并”3种基本操作，逐步调整功能树的结构，最终变形为功能树的析取范式树。

1） 非门下降

根据布尔代数分配律，对功能树中门类型为“与非”或“或非”的非叶子节点，将其非门下移至其子节点，使其本身的门类型变换为“与”或者“或”的过程，称为功能树的非门下降，如表1所示。

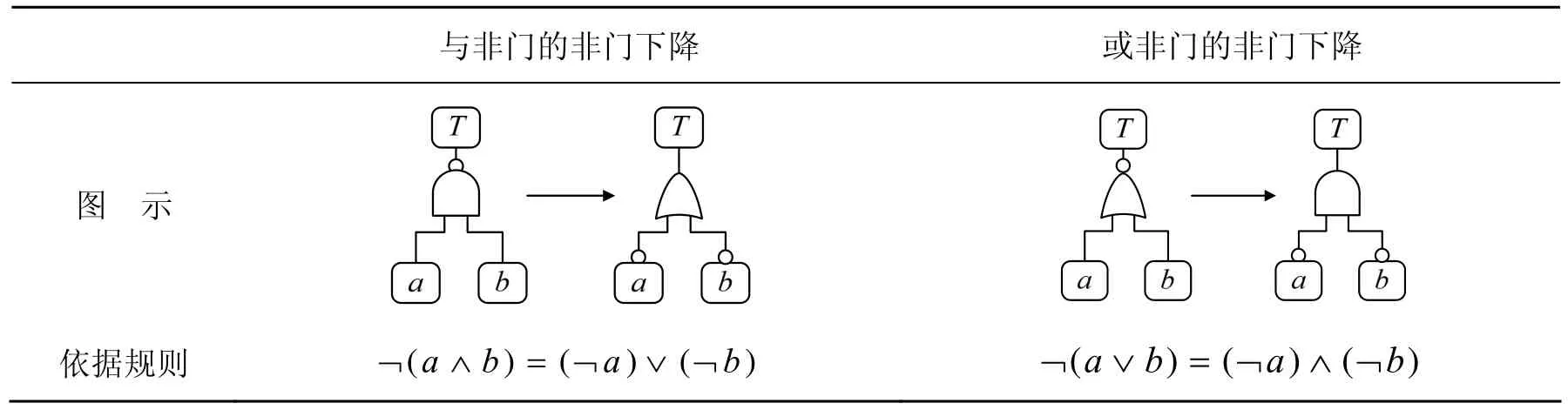
表1 非门下降的规则图示

2） 或门提升

根据布尔代数分配律和结合律，对功能树中门类型为“或”的非根非叶节点，将其或门上移至其父节点，使其父节点的门类型转变或保持为“或”的结构变换过程，称为功能树的或门提升，如表2所示。

表2 或门提升的规则图示

3） 与门合并

根据布尔代数结合律，对功能树中父节点为“与”的非根节点，将其与父节点的与门合并的结构变换过程，称为功能树的与门合并，如表3所示。

表3 与门合并的规则图示

门类型解析法的算法描述中，用户从数据库中读取领域专家建立的功能树后，选定其某一节点T，对以T为根的子树求解其析取范式树。其中，Q是暂存队列，初始值为空。

（1） 若T为空或叶子节点，转（10）。

（2） 查找T的子树中门类型为“与非”或“或非”的节点Temp，若Temp为空，转（5）。

（3） 若Temp不是叶子节点，对Temp执行非门下降，Q.push（Temp所有孩子节点）。

（4） 若 Q为空，转（2）；否则，令Temp=Q.top()，Q.pop()，转（3）。

（5） 查找T的子树中门类型为“或”的非根非叶节点Temp，若Temp为空，转（8）。

（6） 对Temp执行或门提升。

（7） 若Temp->parent不是T，令Temp=Temp ->parent，转（6）；否则，转（5）。

（8） 查找T的子树中父节点为“与”的非根节点Temp，若Temp为空，转（10）。

（9） 对Temp执行与门合并，转（8）。（10） 返回T。

算法的输出是一棵以T为根结点的新子树，即为以T为根的原子树的某一析取范式树，它的结构只可能是两层功能树，或者只有根节点为或门的3层功能树。

结点标识替换法可以对以字符类型记录存储的功能树节点直接操作，通过依次执行“非门下降”、“标识替换”、“规范整理”3种基本操作，对输入端的根节点标识字符进行分裂、替换、整理，得到功能树析取范式形式 φd(X)的全部布尔积项的标识字符串，即可据此建立功能树的析取范式树。

1） 非门下降

此处的“非门下降”与门类型解析法的“非门下降”原理、步骤相同，不再赘述。

2） 标识替换

对功能树中任一节点T，如果该节点不是叶子节点，则查询该节点的门类型和子节点，进行相应字符替换。如果T是与门节点，则替换T为所有子节点的标识字符串；如果T是或门节点，且T有n个子节点，则先将T复制n-1次，再对n个T分别用其n个子节点标识字符进行替换，如表4所示。

表4 字符替换的规则

为方便字符操作，此处叶子节点的非门不以单独的门类型标定，而是直接绑定叶子节点，在其标识字符加上标“’”，例如叶子节点x的非为x'，并将x与x' 看做不同的叶子节点，当x与x'同时出现时，不认为是字符x的重复。

3） 规范整理

潘金莲作为《金瓶梅》中的第一女主角，对其进行分析的文章汗牛充栋。批评家对潘金莲的态度由最开始的深恶痛绝，到后来的深表同情，直至最终保持客观的评论，可以说是一个不断从表层向深层理解的过程。潘金莲是一个典型环境下的典型人物，她追求一切的欲望，小说中许多人物或多或少都有潘金莲的影子。

对任一标识字符串执行“规范整理”，以使所有的标识字符串遵循同一规则，方便多个标识字符串的比较、排序等处理。首先要对节点标识字符串中的节点标识进行“排序”，排序的规则可以依据预先规定的节点标识排列顺序。例如：字符串d, c, a, b, c, a根据字母表顺序排序后得到字符串a, a, b, c, c, d。然后对排序过后的节点标识字符串进行“重复消除”，合并重复出现的标识，确保每个标识在字符串中仅出现一次。例如：字符串a, a, b, c, c, d消除重复后得到字符串a, b, c , d。

叶结点替换法的算法描述中，用户读取功能树后选定某一节点T，求解以T为根的子树其析取范式树。其中，Q是暂存队列，StrQ是布尔积项的字符串存储队列，StrTemp是暂存字符串，初始值均为空。

（1） 若T为空或叶子节点，转（12）。

（2） 查找T的子树中门类型为“与非”或“或非”的节点Temp，若Temp为空，转（5）。

（3） 若Temp不是叶子节点，对Temp执行非门下降，Q.push（Temp所有子节点）。

（4） 若 Q为空，转（2）；否则，令Temp=Q.top()，Q.pop()，转（3）。

（5） StrQ.push(“T”)。

（6） StrTemp=StrQ.top()，StrQ.pop()，查找StrTemp中第1个非叶结点Temp，若Temp为空，转（9）。

（7） 若Temp为与门节点，替换StrTemp中的 Temp为 Temp所有子节点标识的集合，StrQ.push(StrTemp)，转（6）。

（8） 若Temp为或门节点，令n=Temp子节点数量，令StrTemp(i)=StrTemp，其中i=1,2,…,n，分别替换StrTemp(i)中的Temp为Temp第i个子节点标识，StrQ.push(StrTemp(i))，转（6）。

（9） 对 StrQ中所有字符串分别进行标识排序。

（10） 对StrQ中所有字符串分别进行重复标识消除。

（11） 建立以T为根节点的析取范式树。

（12） 返回T。

算法的输出与门类型解析法相同，为以T为根的原子树的某一析取范式树。

3 任意功能树的相似扩展

用可拓学[10]的物元[11]概念表示的功能称为功能物元，物元之间的相似程度为物元相似度，基于人类相似联想和对比联想的物元相似度分别为物元一般相似度和物元对比相似度[12]。

定义4 物元一般相似度 两物元Ra、Rb的特征数量分别为k、l，其中相同特征ci的数量为n，且 Ra、Rb在特征 ci上的特征一般相似度为simi(Ra,Rb)，取ci对相似程度影响的权重系数为ωi，则定义这两物元的相似程度为物元一般相似度，计算方法为

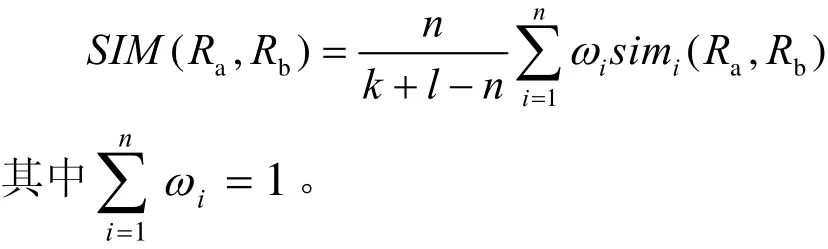
定义5 物元对比相似度 两物元Ra、Rb的特征数量分别为k、l，其中相反特征对cr、ct的数量为n对，且Ra、Rb在特征对cr、ct上的特征对比相似度为 simr′t(Ra,Rb)，取特征对cr、ct对相似程度影响的权重系数为ωi，则定义这两物元的对比程度为物元对比相似度，计算方法为

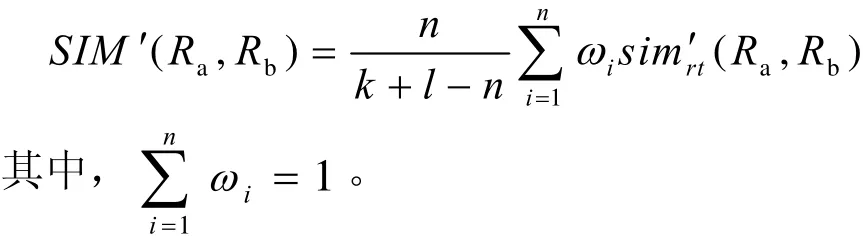
概念设计中，设 ω= (ω1,ω2,… ωn)为领域专家给出的产品物元特征的权重向量，如果则需要重置ωi，令(ω1′,ω2′ ,… ωn′)，显然再取ωi′为权重系数计算物元一般相似度 SIM(Ra,Rb)或物元对比相似度 SIM′(Ra,Rb)。

由于功能树与其析取范式树具有相同的解空间和布尔积项，因此，功能树的相似度计算可以转化为其析取范式树的相似度计算。析取范式树的每个布尔积项对应的子树都是实现顶功能即设计需求的充分条件，可认为是实现设计需求的方案之一，因此计算析取范式树的相似度也就是计算其布尔积项对应的子树之间的相似度。由于析取范式树一般都存在不止一个布尔积项，从而需要计算两棵析取范式树的布尔积项两两之间的相似度，再选取一个特殊值作为两棵析取范式树之间的相似度，习惯上一般选取最大值。

对任意两棵功能树T1、T2进行相似度计算的主要处理过程为：求解功能树T1、T2的析取范式树T1d、T2d；对T1d中的每一个布尔积项对应的子树，分别使用物元相似度计算公式，与 T2d中的每一个布尔积项对应的子树计算物元相似度，并记录；按照预先设置的取值标准，取计算得到的所有物元相似度的最大值、最小值或平均值等作为功能树T1和T2的相似度。

任意两棵功能树T1、T2的相似度计算的步骤如下：

1） 求解功能树T1的析取范式树T1d；

2） 求解功能树T2的析取范式树T2d；

3） 令 i= 1；

4） 查询T1d的第i个布尔积项对应的子树A1i，若不存在，转10）；

5） 令j=1；

6） 查询 T2d的第 j个布尔积项对应的子树A2j，若不存在，转9）；

7） 计算A1i与A2j的相似度；

8） 令j=j+1，转6）；

9） 令i=i+1，转4）；

10） 输出A1i与A2j的相似度的最大值；

11） 结束。

计算功能树的物元一般相似度和物元对比相似度后，判断符合阈值要求，则可进行一般相似扩展和对比相似扩展[12]，获得较原始功能树蕴含更丰富信息的扩展功能树。

4 设计过程的实例

为了展示概念设计中任意功能树的可拓相似扩展过程，以多功能茶杯的设计为例，依次对其功能树进行一般相似扩展和对比相似扩展。

1） 由领域专家根据设计需求进行功能分析，建立初始功能树。图4所示的初始功能树，每个叶子节点下方的编号（如L1）为基本变量编号，每个门节点下方的编号（如 G1）为门变量编号。

2） 以图4中或门节点G6为例，有两个子功能“杯体双层真空”和“杯体反射保温”，查询获得以或门节点G17为根的子树有4个子功能“杯体双层真空”、“杯体保温材料”、“杯体电加热”和“杯体双层中空”，根据任意功能树的相似度计算方法计算G6和G17的物元一般相似度大于阈值，因此将 G17一般相似扩展入功能树中。同理，可对初始功能树进行对比相似扩展。

3） 图5展示的扩展功能树为对初始功能树的多个节点进行一般相似扩展和对比相似扩展后的结果。

图4 多功能茶杯的初始功能树

图5 对比相似扩展后的扩展功能树

扩展功能树较初始功能树所蕴含的信息明显有所增加，表5给出了实例扩展前后的数据分析。

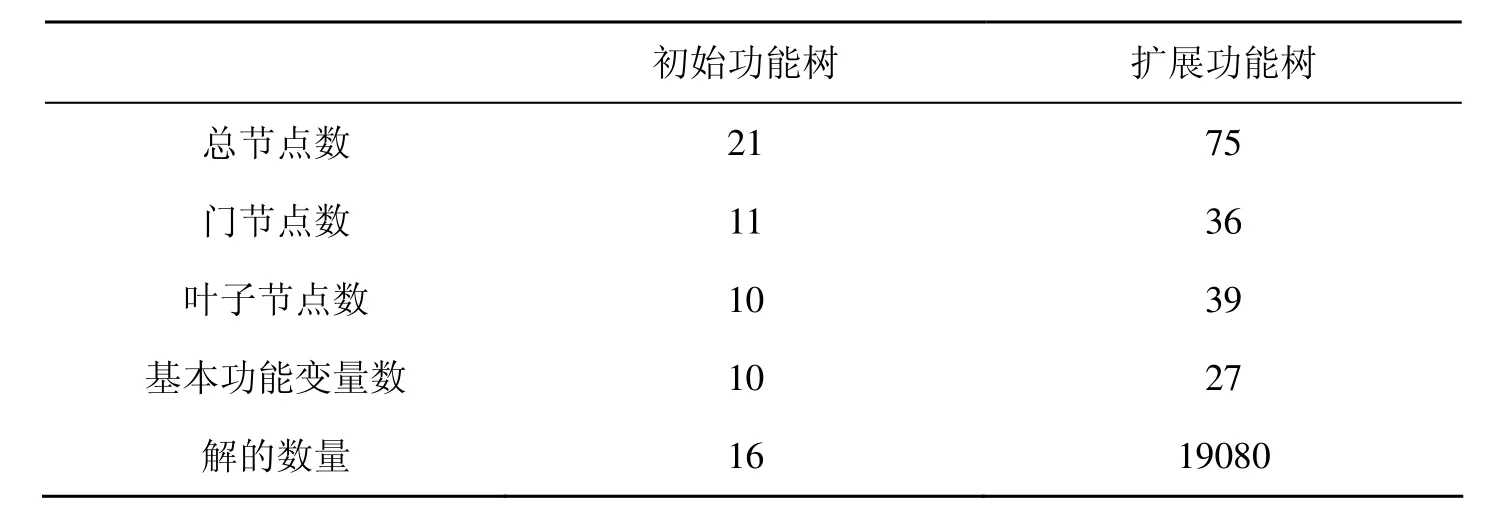
表5 初始功能树与扩展功能树的分析对比表

5 结 论

使用现有功能树相似度计算方法计算包含“与”、“或”、“非”3种门类型功能树的相似度存在着难以逾越的障碍。因此，从功能树与布尔代数的本然联系出发，提出了析取范式树的概念，以及两种求解析取范式树的算法，并描述了使用析取范式树计算任意两棵功能树的相似度的方法。拓展了功能树相似扩展方法的应用范围，扩大了设计解空间，增加了获得创新解的可能性。

析取范式树虽然简化并统一了复杂的功能树结构，然而这种简化必须以删除中间节点及其信息为代价，对于强调中间节点信息的设计过程不适用。

[1] Hsu W, Liu B. Conceptual design: issues and challenges [J]. Computer Aided Design, 2000, 32(14): 849-850.

[2] Chakrabarti A, Thomas P, Bligh A. Scheme for functional reasoning in conceptual design [J]. Design Studies, 2001, 22(6): 493-517.

[3] Li Wenqiang, Li Yan, Wang Jian, el at. The process model to aid innovation of products conceptual design [J]. Expert Systems with Applications, 2010, 37(5): 3574-3587.

[4] Li Biqiong, Li Jie. Expert systems research for conceptual design of drilling fixture based on fuzzy algorithm [C]//Proceedings of 9th International Conference on Computer-Aided Industrial Design and Conceptual Design, 2008: 259-262.

[5] Zhang Hao, Zhang Jianhua, Liu Nian, el at. Function-oriented information assets identification on substation automation systems [C]//Proceedings of Asia-Pacific Power and Energy Engineering Conference, 2009: 1-4.

[6] Liu Xiaoping, Qin Jin, Tang Yiming. An innovative function-tree building method based on similarity theory and extension theory [C]//Proceedings of 7th International Conference on Computer-Aided Industrial Design and Conceptual Design, 2006: 1-6.

[7] 刘晓平, 陆劲挺, 唐益明. 基于可拓学的对比相似功能树扩展方法[J]. 工程图学学报, 2009, 30(1): 153-159.

[8] Zhou Meili. Principles of modeling of similar systems and feasibility analysis [J]. Journal of Systems Science and System Engineering, 1997, 6(4): 439-443.

[9] 左孝凌, 李为鑑, 刘永才. 离散数学[M]. 上海: 上海科学技术文献出版社, 1982: 266-268.

[10] Zhu Qinhua, Yu Yongquan, Cai Wen. Extension set and the research of the extension ADD transformation [C]// Proceedings of 3rd International Conference on Information Technology and Applications, 2005: 399-402.

[11] Ju Yijing, Yu Yongquan, Ju Guangming, el at. Extension set and restricting qualifications of matter-elements' extension [C]//Proceedings of 3rd International Conference on Information Technology and Applications, 2005: 395-398.

[12] 陆劲挺. 概念设计中功能树可拓相似推理方法研究[D]. 合肥: 合肥工业大学, 2009.

Method on similar extension of arbitrary function trees based on matter-element theory

Liu Xiaoping, Lu Jingting
( VCC Division, School of Computer & Information, Hefei University of Technology, Hefei Anhui 230009, China )

Function models are the core objects of conceptual design. Function tree is a typical function model which is widely used. Defects are found while the similarity of arbitrary function trees is calculated by existing method. Therefore, the concept of disjunctive normal form tree is proposed based on Boolean algebra. After that two solutions of Disjunctive normal form tree are presented. And a method on similarity calculation of arbitrary function trees is described. Thus, the application of function trees’ similar extension is expanded. As a result, the solution space is enlarged, and the possibility to attain innovational solutions increases. At last, an application example demonstrates the effectiveness of the method.

computer application; function tree; disjunctive normal form tree; matter-element similarity degree

TP 391

A

2095-302X (2012)04-0042-08

2010-12-31

国家自然科学基金资助项目（60673028）

刘晓平（1964-），男，山东济南人，教授，主要研究方向为计算机图形学、计算机辅助设计。