超大型三维有限元模型的快速可视化算法
邹 静, 纪洪广
(1. 清华大学水利水电工程系,北京 100084;2. 北京科技大学土木与环境学院,北京 100083)
超大型三维有限元模型的快速可视化算法
邹 静1,2, 纪洪广2
(1. 清华大学水利水电工程系,北京 100084;2. 北京科技大学土木与环境学院,北京 100083)
针对超大型三维有限元模型的特点,总结了其可视化任务的基本需求和关键算法。由此分别为网格、单元、剖面可视化,以及绘制彩色云图等不同任务,编制了结构简单、运行可靠的快速显示算法。通过具体工程实例与典型商业程序的对比验证,初步证明了该算法的可行性和优越性,有助于简化超大型有限元程序的编写过程。
三维有限元; 可视化; 彩色云图; 实体切割
随着矿山开采实践的不断深入,三维数值分析以强大的分析能力逐渐成为主流。由于实际工程尺度的加大,三维计算模型的规模快速增长。近年来,单元数从十年前的数千增长到数万,进而增加到数十万甚至超越一百万。即使不考虑本构模型复杂化的情况,矿山岩土分析也因此面临很大压力。如何快速、可靠地求解这些模型,是很有实际意义的问题。而在这些问题中,基于“所见即所得”的分析与测试需要,计算模型构造与成果的快速可视化,是一个无法逾越的重要环节。尽管基本的算法和思路已不鲜见,不少软件与程序包也已实现相应功能。但要么程序过于庞大,要么源代码受保护,编写简单高效的可视化模块始终存在不小挑战。原有算法或程序虽然在原理上依然正确,但由于先前缺乏相应的针对性,难免暴露问题出现反应迟钝的现象。在各种分析方法中,以有限元方法算法最成熟,同时其三维计算模型结构简单,并且可与很多分析方法通用网格。因此,本文以有限元计算模型为研究对象,在实践基础上针对模型规模超大的情况,总结出关键、核心的算法需求,进而构造出简洁、高效的可视化实现流程。本项研究不仅有助于数值计算研究的进展,对工程图形领域的研究也有一定的借鉴意义。
1 核心算法
1.1 算法需求分析
有限元乃至其他算法三维模型的显示,无外乎包括显示要素与结果两个方面。要素即几何要素,包括:点、网格、单元等。结果即计算结果,显示方式等:云图、切片、等值线图等几种。可以认为可视化任务的本质是:表示基本元素及其连接关系。在超大规模有限元模型的背景下,最紧要的莫过于:省略不可见元素,抽取关键要素,从而有效降低绘图工作量。据此,可将算法需求分为以下两大类:
1) 去除重复元素
在计算模型规模较小的情况下,可以根据元素的拓扑构造完整地汇出图形。即四面体单元绘成6条边、4个面,或者块体单元显示为12条边、6个面,绘制元素数量为单元数的数倍之多。在这些元素当中位置重叠而不可见的占大部分,必须显示的元素实际常不到总数的1/10。因此,当计算模型规模十分庞大时,在元素序列中快速删除重复元素,是加快绘图速度一项十分重要的算法需求。
2) 明确元素间连接关系
边的绘制取决于点的连接关系,面的绘制取决于边的连接方式,而显示实体则要涉及面的邻接关系。各种关系当中以边的邻接关系,也就是顶点的连接顺序最为重要,切片图和等值线图都要依此为基础。具体明确点素间连接关系方法,用数学语言描述实际如图1所示,即为无向图的深度优先遍历。
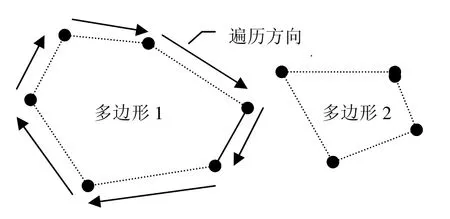
图1 无向图的深度优先遍历
1.2 关键算法选择
根据上面总结的算法需求,结合C/C++语言与 Opengl功能的特点,几个关键算法可以归纳如下。
1) 快速排序
使用排序可将相同元素移到相邻位置,然后在只要从头至尾比较前后位置,即可检测到所有内容重复的元素。如果操作大尺度元素序列计算量必然巨大,此时可采用快速排序算法[1]来处理。虽然采用查找再插入的常规方法可在空间复杂度上占优势,但其时间复杂度大致为(1/800~1/8)O(n2),当元素很多时远大于快速排序的O(n)。在各种现有的快速排序实现当中,以C语言的qsort库函数速度最快且性能最为稳定。该函数由stdlib.h文件引用,具体调用方式为:
_CRTIMP void __cdecl qsort(void *, size_t, size_t, int ( __cdecl *) (const void *, const void *));
参数1为待排序数据块的首地址,参数2为数据块单元个数,参数3为数据块的单元尺寸,参数4为自定义的单元比较函数,输入参数为单元首地址,输出变量为表示单元大小关系的整数。
假设数列的元素长度为n,且已经为每个元素的组成要素排序,则元素E1、E2的比较函数算法可表述如下:
for i 1 to n
if E1[i]> E2[i]
return 1
else if E1[i]< E2[i]
return -1
end
end
return 0
其中,返回1表示E1> E2,返回-1表示E1< E2,而0表示E1= E2。
2) 深度优先遍历
由于邻接表(见图2)主要用于绘制切片,本文无向图的节点数不会超越 12个,一个节点所连的边数也不会超过3个。因此,选择12×12的整数数组来表示,其具体的构造方式如图所示,深度优先遍历全图的流程如图3所示。
添加边(i, j)的算法为:
l ←K(2, i)
K(l, i)←j
K(2, i)←K(2, i)+1
K(3, i)←K(3, i)+1
l ←K(2, j)
K(l, j)←i
K(2, j)←K(2, j)+1
K(3, j)←K(3, j)+1
删除边(i, j)的算法为:
l
←K(2,i)
K(l, i)←-1
K(3, i)←K(3, i)+1
l ←K(2,j)
K(l, j)←-1
K(3, j)←K(3, j)+1

图2 邻接表构造
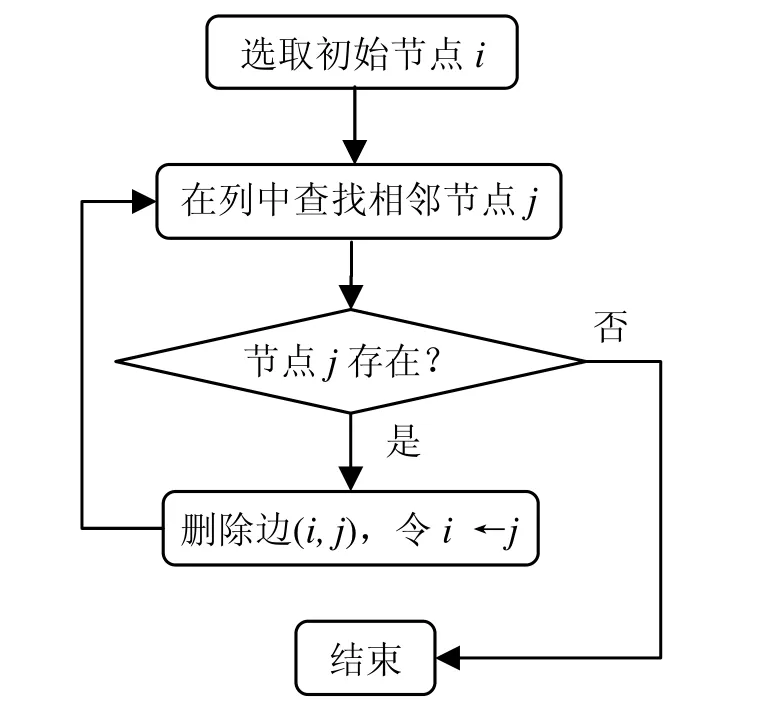
图3 遍历无向图流程
3) 图形显示
本文图形显示过程如图4所示,先生成矢量模型再调用 Opengl绘制图形,以免单元、节点数据过多造成绘图缓慢。其中用到的Opengl线、面绘制语句,以及若干绘图模式设定语句,可以归纳汇总如下:

图4 绘图过程
绘制线条:
glBegin (GL_LINES);
glColor3f(1.0f,1.0f,1.0f);
glVertex3f (x1,y1,z1);
glColor3f(1.0f,1.0f,1.0f);
glVertex3f (x2,y2,z2);
glEnd ();
绘制面:
glBegin (GL_POLYGON);
glColor3f(1.0f,1.0f,1.0f);
glVertex3f (x1,y1,z1);
…
glEnd();
绘制云图时采用平滑模式:
glShadeModel(GL_SMOOTH);
为了显示正确的三维效果,调用以下两条语句启用深度测试:
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LESS);
由于线消隐与面消隐机制存在差异,同时绘制面与其边线时常出现线被面掩盖的现象。文献[2]中采用面模拟线的方法回避这个问题,而笔者经尝试后发现:如果先绘线再绘面并启用线平滑模式,也能较好地解决问题。调用线平滑模式的语句如下:
glEnable(GL_LINE_SMOOTH);
glHint(GL_LINE_SMOOTH_HINT,
GL_FASTEST);
2 典型可视化任务的实现算法
有限元和其它数值计算方法中,最典型的可视化任务有:节点、网格、单元与切片的可视化,以及数据云图绘制等4种类型。相应的实现算法简述如下,单元具体构造参见有关经典算法[3-4]。
2.1 网格可视化
网格可视化的关键如图5所示。先根据单元构造绘出所有边线,再合并位置重叠(实为端点编号重合)的边线,从而生成可以透视的骨架网格。令数组e[1…ne]代表边线集合,则网格可视化伪代码可表述如下。为了准确比较e[i]和e[l]大小,已先为边线节点排好顺序。
l←0
for i 1 to ne
if e[i]≠e[l]
wend: 绘制边线e[l]
l←i
if i=ne
goto wend
end
end
end

图5 边线合并
2.2 单元可视化
单元可视化重点在于外表面的可视化,实际上就是显示单元群外壳的过程,所以单元可视化可归结为图6所示的外壳抽取[5-6]过程。具体操作方法为:先根据单元构造生成面元列表f [1…nf ](其元素为排序后的面节点编号),然后由快速排序将相同面移到相邻位置,再由下面伪代码如下表述的算法,删除重复面元抽取外壳绘成图形。

图6 外壳抽取
l←0
for i 1 to fe
if f [i]≠f [l]
wend:按照存储的节点顺序,重排f [l]的节点次序
绘制边界面f [l]
l←i
if i=nf
goto wend
end
else
i←i+1
l←i
end
end
需要注意的是,使用 Opengl同时绘制大量线与面时,绘制线比绘制面会消耗更多时间,因而往往会明显拖慢绘图的整体速度。因此,还需要按照上一小节的方法,删除多余边线抽取表面网格单独绘图。
2.3 云图绘制
云图绘制核心算法与上一小节基本相同,区别在于后者只给单个面绘上单一颜色,而前者则需要根据数值绘成渐变颜色。超大型有限元模型的单元已经足够密集,不需要像文献[7]一样布置精确的颜色方案。只需为每个顶点设定单独颜色值即可,数值选择取则决于节点变量值的相对大小。从而,首先确定绘制的变量是否为节点变量,如果为单元变量则还需要转化类型。然后,按照一定规律确定颜色值集合——也即色谱,根据变量相对值选定颜色数值即可绘制云图,简要的操作流程如图7所示。

图7 云图绘制流程
研究matlab工具箱的.m源文件,可以得到常见色谱的计算方法。其中,灰度色谱计算式如式(1)所示,中n表示色谱的长度,而r、g、b分别表示三基色数值(取值范围为[0,1])。

hsv色谱的计算式如下式(2)与式(3)所示
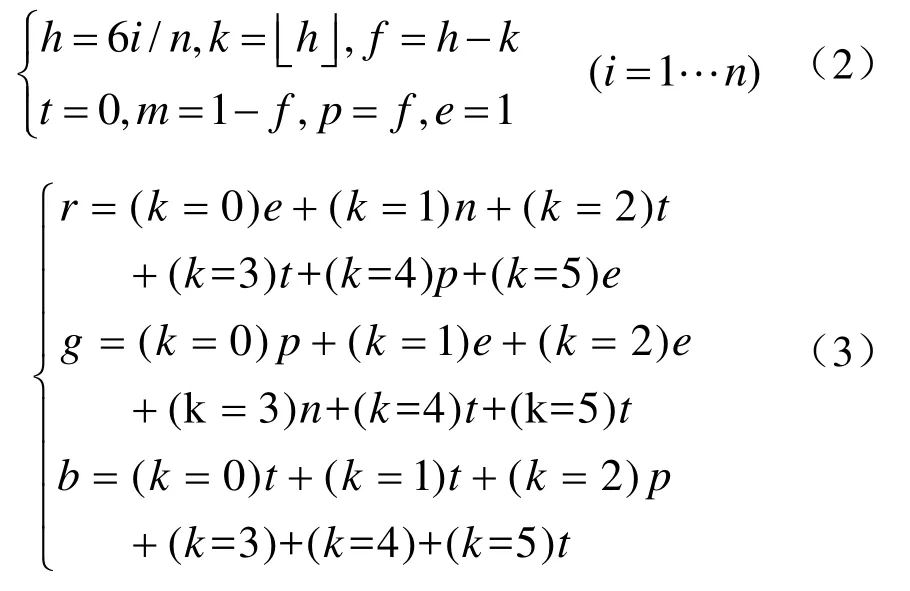
2.4 剖面可视化
制作切片的方法大致有:文献[8]所述的直接切割单元法,以及文献[9]调用Opengl的图像剖切法。后者算法较为复杂且难以输出剖面数据,本文采取前一种方法的思路,但对各种类型单元使用同一切割方案,不再区分不同的相交情况。主要思路如图8所示:查找与剖面相交的单元,然后逐一剖切再组合成完整的剖面。判断一个单元是否与剖面相交,根据其在剖面上下侧是否均有其节点。给定节点(x, y, z)与剖面A(x-x0)+B(y-y0) +C(z-z0)+D=0,相应位置关系判计算方法见式(4)

其中,d>0表示点在剖面上侧,d=0表示点在剖面中间,d<0表示点在剖面下侧。
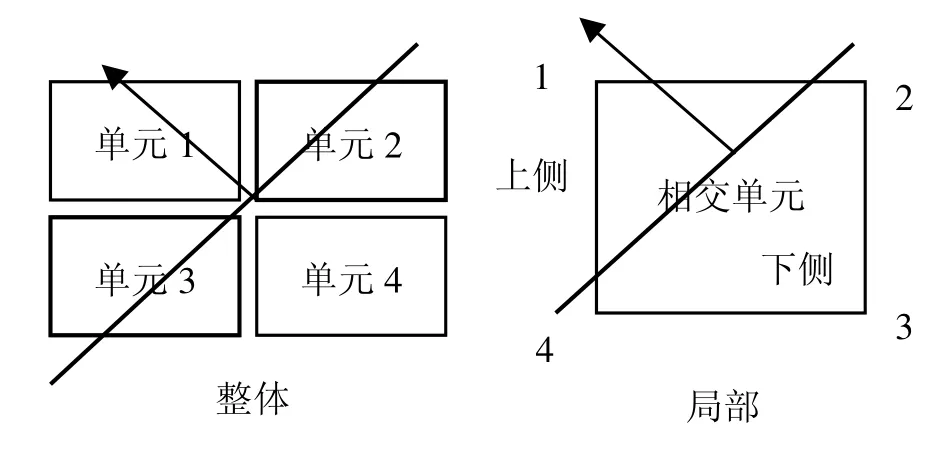
图8 相交单元检测
在作数据切片时需要插取交点数值,仅作单元切片时则不需要插值,具体操作步骤简述如下:
Step 1 计算节点与剖面的位置关系,据此抽取所有与剖面相交的单元,记录单元编号集合成数组。
Step 2 释放所有单元边线形成交线数组,同时在单元数组中记录边的编号,以及其在单元内部的编号。
Step 3 删除重复元素紧缩边线数组,并更新相交单元数组对应编号。
Step 4 计算每条边与剖面的交点,同时插取交点处数值,并记录成交点数组。
Step 5 逐个单元归纳交线,构造并填充交点邻接表。
Step 6 遍历交点邻接表形成单元剖面,然后组合成最终的模型剖面。
3 应用实例
为了验证本文算法的实际性能,选取以下3个实例与现有同类软件作对比试验。实现语言为C++且混合使用devcpp 5/vc++ 6.0编程,编译环境是32位Windows Vista Business系统。机器配置为:Intel 酷睿 2.4GHz双核处理器, 频率1066MHz的2G容量DDR3内存,频率475MHz、1G容量集成显卡。
1) 规则网格
本算例几何尺寸为 1×1×1m,单元划分尺寸100×100×100,共计100万个八节点规则单元。最终运算所得单元、网格图形如图9所示,为了保持图形纸面清晰程度网格只展示平面图形。当采用大型商业有限元程序 ANSYS对比时,不但生成网格明显吃力,而且启动单元图形也十分迟钝(15s以上),而运行本文算法时则没有此类问题。
2) 自由网格
本算例为起伏的地表模型,使用网格自由划分工具tetgen(网址为:http://tetgen.berlios.de/)划分网格,得到单元数 842245、节点数 149885的全四面体网格模型。根据本文算法得到的图形如图10所示,其中剖切面为过模型中心点且垂直于X轴的平面,绘图视线方向平行于X轴正方向。本文算法显示这些图形基本流畅,当将其导入岩土工程常用数值计算工具Flac3D,发现绘制单元或云图大致需要3秒的反应时间。
3) 复杂网格
图11是以某矿的实际地下巷道为基础,采用tetgen划分出的复杂四面体网格,总计节点数164681而单元数为588129。其中,图11(a)图为整体单元图形,图11(b)图为前者方框处放大结果。该模型的特点为节点数相对较多,所以单元边线数量十分巨大。使用tetgen自带可视化工具tetview查看时,移动、转动模型有些迟钝(有时停顿 10s以上)。而如果使用基于本文算法编制的工具,则生成、防缩、移动以及转动模型都基本流畅。
4 结 论
从上面的对比实验可以看出:本文算法不仅能正确完成指定功能,而且在运行速度、稳定性上优于一些现有商业软件或免费工具。如果再充分调用 Opengl的图形加速功能,算法的运行速度还能进一步提升。因此,本文算法能更好满单元数量不断增长的需求,并且算法结构简单容易实现,可在面向超大型三维数值模型的有限元(或他方法)程序编制时使用。

图9 简单网格

图10 自由网格
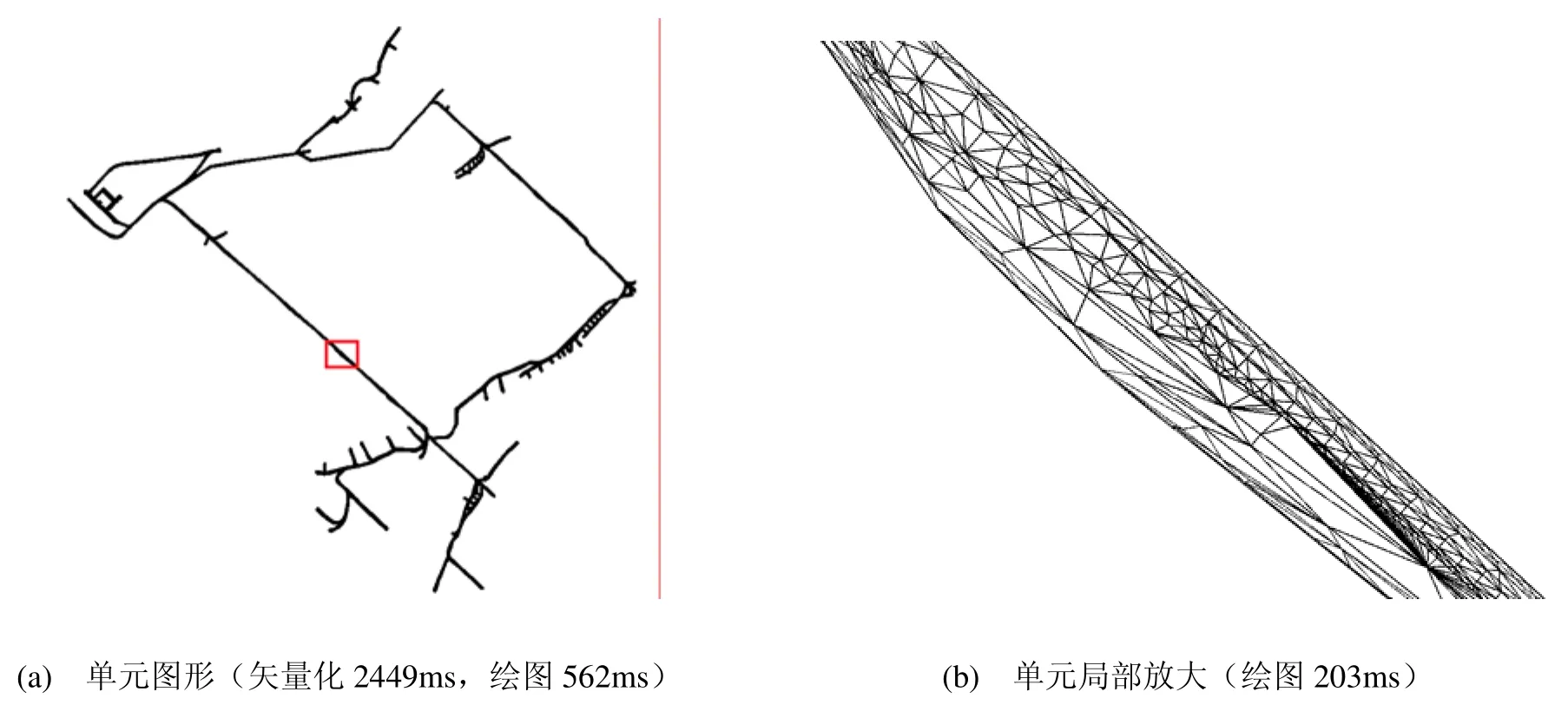
图11 复杂网格
[1] 朱经纬. 三维数据场的三维重建与模型的虚拟切割研究[D]. 武汉: 华中科技大学, 2007.
[2] 周国祥, 王春艳. 基于 OpenGL 三维非均匀 FDTD网格图形的消隐处理[J]. 计算机应用研究, 2008, 25(1): 285-287.
[3] Smith I M, Griffiths D V. Programming the finite element method [M]. Chichester, UK: John Wiley & Sons, 2004: 587.
[4] Liu G R, Quek S S. Finite element method: a practical course [M]. London UK: Butterworth-Heinemann Publications, 2003: 184.
[5] 陈良玉, 杨文通. 一种大型三维有限元网格的显示和高效消隐方法[J]. 计算机辅助设计与图形学学报, 1997, 9(2): 164-167.
[6] 余卫平. 有限元网格图形处理技术及计算结果的可视化[J]. 计算机辅助设计与图形学学报, 2003, 15(12): 1561-1565.
[7] 李建波, 陈健云, 林 皋. 针对三维有限元数据场的精确后处理算法[J]. 计算机辅助设计与图形学学报, 2004, 16(8): 1169-1175.
[8] 梁振光, 唐任远. 电磁场有限元结果的剖切显示[J].电机与控制学报, 2004, 8(3): 242-246.
[9] 杨晓松, 顾元宪, 李云鹏, 等.有限元网格体绘制中的剖切算法[J]. 中国图象图形学报, 2002, 7(1): 55-62.
Fast visualization algorithm for huge 3D-finite element models
Zou Jing1,2, Ji Hongguang2
( 1. Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China; 2. School of Civil & Environment, Beijing University of Sciences & Technology, Beijing 100083, China )
According to the features of huge 3D-FEM models, basic requirements of visualization and key algorithms are summarized. Then, a simple and reliable algorithm of fast rendering is prepared for different tasks of grid, unit, slice visualization and color contour respectively. Through contrastive testification of specific examples and typical business software by contrast, the feasibility and superiority of the algorithm is initially demonstrated, which can contribute to simplification of preparation for huge FEM program.
3D-FEM; visualization; color contour; solid cutting
TP 391.72
A
2095-302X (2012)04-0013-07
2010-07-02
国家“863”重点课题资助项目(2008AA062104);“十一五”支撑课题资助项目(2008BAB33B03);国家“973”重点课题资助项目(2010CB226803,2010CB731501)
邹 静(1982-),男,湖南新化人,博士,主要研究方向为力学数值计算程序的可视化算法设计。

