TPU/POE共混体系的热解动力学研究

李 冲，魏永春，何晓红，廖正福，陈旭东

（1.北京理工大学珠海学院，广东 珠海 519085；2.广东工业大学材料与能源学院，广东 广州 510090；3.中山大学化学工程学院，广东 广州 510275）

热塑性聚氨酯树脂(TPU)，既具有橡胶的强度高、弹性好、耐磨及耐油性优良等物理性能，又有塑料的力学性能高，使用工艺简单等优点，应用范围十分广泛。但是TPU存在耐老化性差、蓄热性较高、湿表面磨擦系数低、易打滑、成本较高等缺点[1]。聚烯烃加入到TPU中能够提高TPU的力学性能（如模量、拉伸强度、硬度）和加工稳定性，降低成本。而国内文献中对于TPU/POE共混体系热降解行为研究较少，因此本文通过热重分析仪研究TPU/POE共混体系热降解行为，以期能为制备性能优良的TPU/POE合金材料提供理论参考。

1 实验部分

1.1 主要原料

热塑性聚氨酯TPU[polyester thermoplastic polyurethane elastomer，牌号 S85A，熔融指数 MI为3g·(10min)-1]，是一种聚酯型嵌段共聚物，有硬段和聚酯软段两部分组成。POE(ethylene-octylene copolymer，牌 号 8150，密 度 0.868g·cm-3)是 DOW公司1994年采用新型“限定几何构型”茂金属催化剂单点催化活性INSITE技术合成的乙烯-辛烯共聚物。马来酸酐(MAH，分子量98.02），

1.2 主要仪器

NetzschTG-209热重分析仪，温度范围：30~800℃；温度精确度：±0.1℃；最大称重：1g；称重分辨率：10-6g；升温速度：0.1~40℃·min-1；冷却时间：<15min；真空度：2Pa。

1.3 样品的测试

采用热重分析仪研究TPU等物质,测试气氛为氮气，样品用量5~8mg，氮气流量20mL·min-1，升温速率分别为 10K·min-1，20K·min-1，30K·min-1，40K·min-1，升温范围：室温~700℃。

2 结果与讨论

2.1 热解动力学研究

在TG 曲线上取基础数据，其中分解百分数为α，相应的温度为T(K) ,变化率为dα/dT，氮气流量为20mL·min-1，升温速率β为20K·min-1。

Table.1 从TPU的TG曲线上取的基础数据

运用热分解反应动力学动态实验数学处理方法微分法中的Sharp法[3]和积分法中的Coats-Redfern法[4]对基础实验数据进行分析。

Sharp法：

Coats-Redfern法：

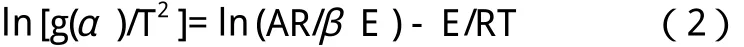
选取16种不同的动力学函数（表2）[5]f(α)和g(α)分别代入式（1）和式（2），以ln [(dα/dT )/f(α)]及ln [g(α)/T2]对1/T分别进行线性拟合，求得不同动力学函数的动力学参数E、lnA值及相关系数γ，计算结果列于表3。

比较上述16种不同动力学函数的动力学参数，发现编号为6、7两种函数，两种方法计算的E， lnA值比较接近，相关系数γ也较好。为确定该热分解反应的动力学函数和反应机理，再用积分法中的Doyle-Zsako法[6]对上述2种函数(6、7) 进行线性拟合，拟合结果E、lnA值及相关系数γ列于表4。

亦可改写为：

由于夏季气温过高，影响导致进风口气温过高。基于此种情况，我们可以选择在进风口进行制冷处理。可以使用脉外低温巷道降低入风温度、对进风风流采用冷水逆流喷淋降温等技术处理。比如可以向矿山的进风井中进行低温水逆流喷淋(武安-30喷雾器)。当进风量为12m/s,温度为26℃,喷水量为40t/h时,这时候温度可以降低2.2～2.6℃。如果是采用冰块与27℃水混合的冷却水在工作面进行风筒喷雾,这时候能够使工作面的入风温度平均下降5.5～6.5℃,相对湿度由原来的40%增加到50%,耗水量约0.24L/min。这种技术降低了夏季的入风气温,效果很好。

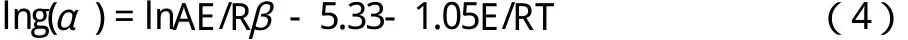
表2 各种微分和积分形式的动力学函数

表3 非等温热分解反应动力学参数

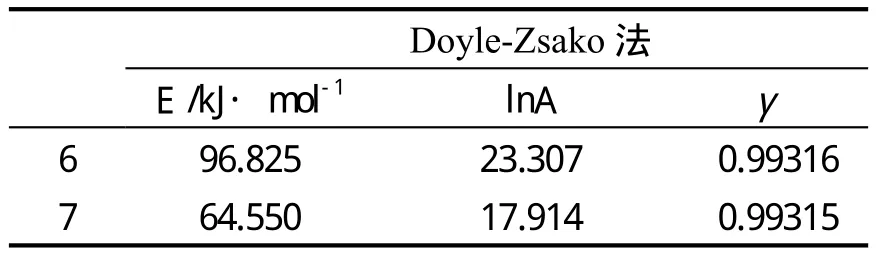
表4 Doyle-Zsako 法线性拟合结果动力学参数

比较表2和表3中的E、lnA值及相关系数γ，编号为6的函数为该热分解反应的动力学函数，即Avrami-Erofeev方程，f(α)=(1-α)，g(α) =-ln (1-α)。因此，该热分解反应机理是成核和生长(n=1)。非等温热分解反应动力学方程为dα/dT=A/βe-E/RT(1-α)。由f(α)=(1-α)，g(α)=-ln(1-α)函数计算的动力学参数结果在一般固体化合物热分解反应动力学参数(E：80~250kJ·mol-1，lnA：16.91~60.09[7])范围内，说明所得到的动力学方程是合理的。

根据动力学补偿效应方程[8]：

a、b为补偿参数。利用表7中数据，进行lnA-E线性拟合，求得补偿参数a= 0.182,b=-2.942。动力学补偿方程为：lnA =0.182E-2.942b。由于动力学补偿参数与实验因素无关，因此补偿参数表征着热分解反应本身的特征。

TPU 的 活 化 能 为 96.825 kJ·mol-1，lnA 为23.307，相关系数为0.99316。

2.1.2 多升温速率动力学

为了解释材料的热降解性能，知道并了解材料的一些相关动力学参数(如Ea、A)是很有必要的。文献报道计算活化能的方法通常主要分为两类：多加热速率法和单加热速率法。其中多加热速率法有Kissinger法[9]，Flynn,Wall[10]和 Ozawa(F-W-O) 法[11]，Friedman-Reich-Levi法[12]，Coats-Redfern 法[13]，Criado法[14]等。本文所用到的是多加热速率法中的Kissinger法，因为Kissinger法相对其它的方法较简单，它不需要知道反应级数n，也不需要知道精确的动力学反应机理，只要知道不同的加热速率β和其最大降解速率所对应的温度Tm就可以求出活化能[15]。

Kissinger法可由方程（7）表示：

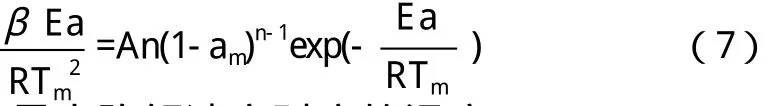
式中：Tm－最大降解速率对应的温度，K；

αm－最大反应速率时的分解百分率；

n－反应级数。

Kissinger法将n(1-αm)n-1看成1且为一个与加热速率无关的量，这样由方程（7）可推导出方程（8）。

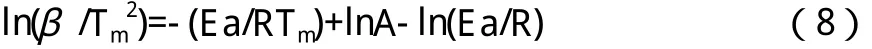
由方程（8）所得，从斜率、截距可分别计算出Ea、lnA，本文首先用Kissinger法求出POE-MA(NH2)的Ea和lnA。

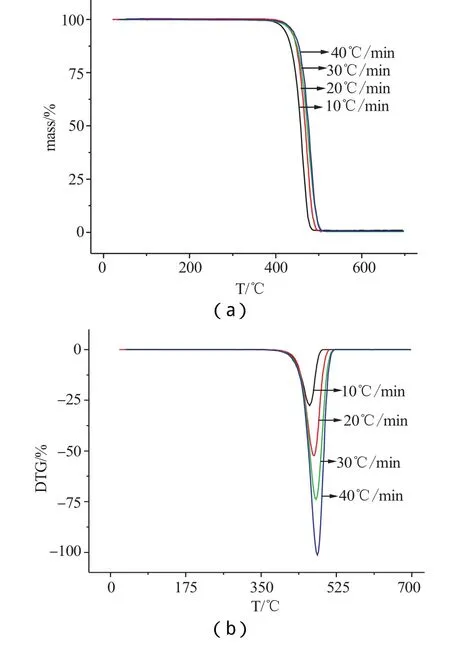
Fig.1 TG and DTG curves of POE-MA(NH2) at different heating rates in N2

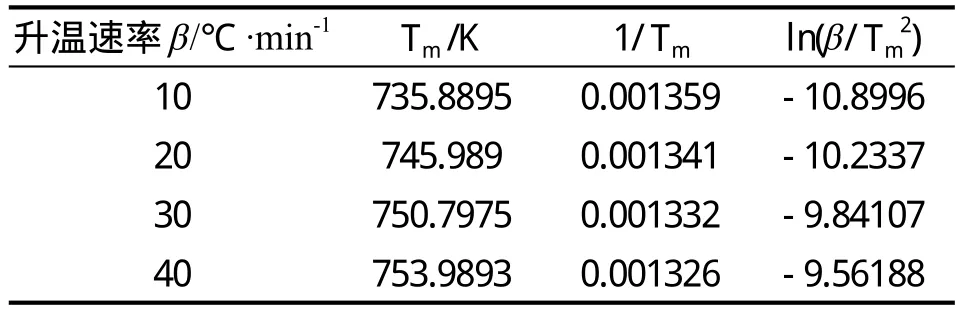
表5 Kissinger法得到的POE-MA（NH2）相关参数

Fig.2 Kissinger method applied to experimental data of at different heating rates of POE-MA(NH2)

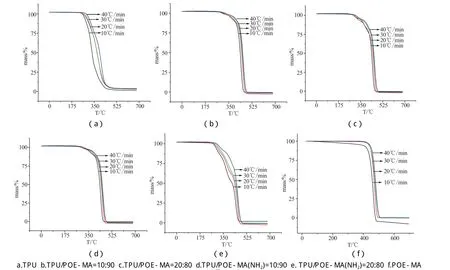
Fig.3 TG curves at different heating rates in N2

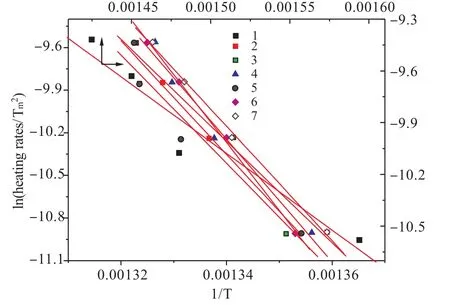
Fig.4 Kissinger method applied to experimental data of at different heating rates of sample1~7

用同样的方法也求出其它样品的活化能Ea、lnA以及R并把它们列于表6中。

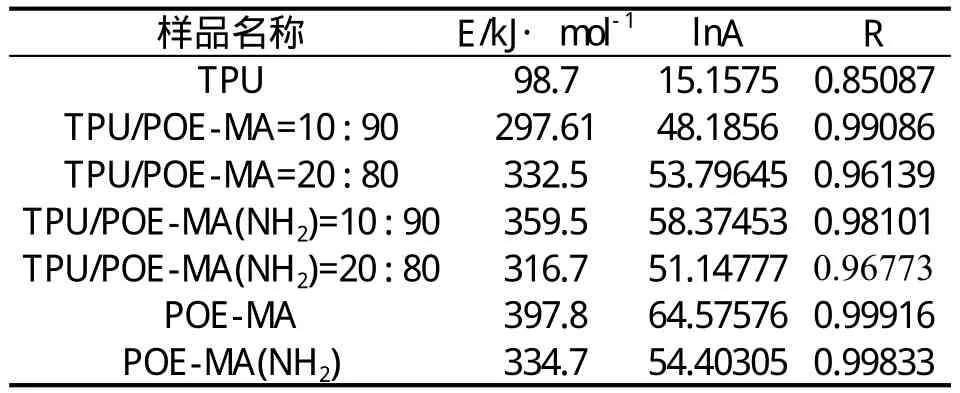
表6 Kissinger 法得到的各样品的活化能，lnA以及相关系数R

由于一种方法很难能令人信服，所以本文用Ozawa(F-W-O)法来比较和佐证Kissinger法得到的结果。Ozawa(F-W-O)法的也不需要知道反应级数n和热解动力学反应机理而只要知道不同的升温速率β及不同分解百分率α时的温度T就可以计算出体系的热解活化能；并且此方法的可取之处是，只要β取足够多的点就可以比较多地计算出同一个样品的活化能，然后求出平均值以减少误差。Ozawa(FW-O)法可由方程（9）表示：

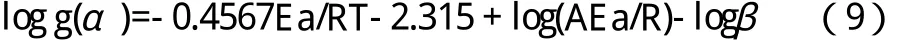
式中：g(α)－转化率函数的积分形式；

Ea－静观活化能，kJ·mol-1；

A－指数前因子；

β－加热速率，℃·min-1；

R －气体普适常数，J·(mol·K)-1；

T－绝对温度，K。

若加热速率不同转化率相同，由方程（9）可推导出方程（10）：

logβ=-0.4567Ea/RT-2.315+log(AEa/R)-log g(α) （10）

对于不同的转化率，log β与1/T的相关性表现为直线，表观活化能可由直线的斜率计算得到[以下用Ozawa(F-W-O)法得到的活化能全部为平均值]；这里还是首先用Ozawa法求出POE-MA(NH2)的活化能。

Fig.5 Ozawa(F-W-O) method applied to experimental data of at different heating rates of POE-MA(NH2)

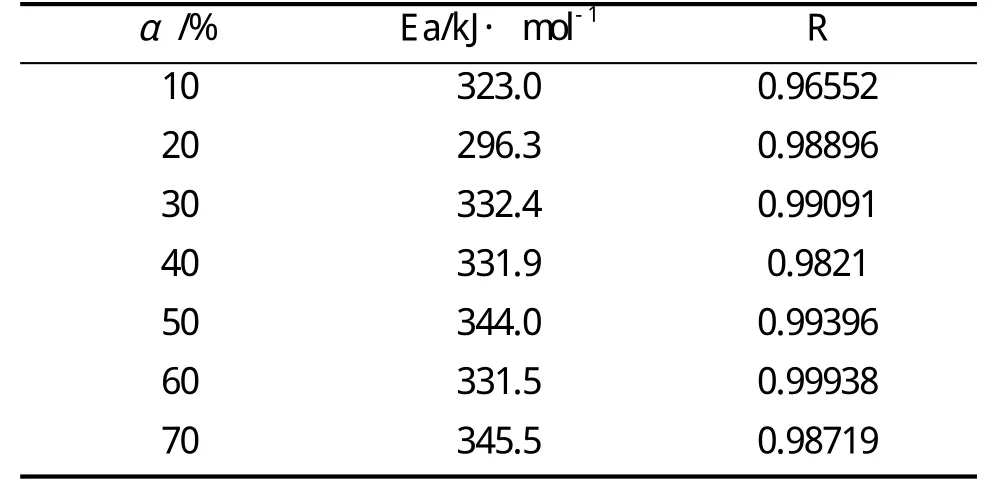
表7 Ozawa(F-W-O)法计算得到的POE-MA(NH2)的Ea和R

本文也用同样的方法求出其它样品的活化能Ea并列于表8中。

表8 Ozawa(F-W-O)法所得到的各样品的活化能

比较Kissinger 法和Ozawa(F-W-O)法计算出的各样品的活化能，纯的POE-MA和POE-MA(NH2) 热解活化能比纯的TPU的热解活化能大很多，而且TPU/POE-MA和TPU/POE-MA(NH2)共混物的活化能介于纯的TPU、POE-MA和POE-MA(NH2)之间；并且除了样品6(POE-MA)热解活化能相差较大外，其余样品的热解活化能用上述两种计算得到的结果基本还比较吻和，说明本文选择的两种活化能的的计算方法[Kissinger法和Ozawa(F-W-O)法]还是比较适合TPU/POE这个体系的。

3 结论

通过热重分析仪对TPU、POE-MA、POE-g-MA(NH2)以及TPU/POE-MA和TPU/ POE-g-MA(NH2)共混物的热降解行为进行了研究，对于TPU用单升温速率法及多升温速率法计算了TPU的热解活化能，发现两种方法都比较适合；对所有样品用多升温速率法计算热解活化能，发现除样品POE-MA外，用Ozawa(F-W-O)法与Kissinger法计算的结果都比较吻合，因此上述两种活化能的计算方法都比较适合该体系。

[1] 山西省化工研究所.聚氨酯弹性体[M].北京：化学工业出版社，1985.21.

[2] 王晓晗，卢冠忠，黄仲涛.VO(H2PO4)2热分析研究[J].化学世界，1999，（2）：68-72.

[3] Wendworth S A,Sharp J H.Kinetic analysis of thermogravimetric data[J].Anal. Chem.，1969，41（14）：2062.

[4] Coats A W ，Redfern J P. Kinetic Parameters from Thermogravimetric[J]. Nature (London )，1964，68： 201-202.

[5] 李余增.热分析[M].北京：清华大学出版社，1987. 94-108.

[6] Doyle C D. Kinetic analysis of thermogravimetric data[J]. J Appl. Polymer Sci.，1961，5（15）：285-292.

[7] Hu R Z，Yang Z Q，Ling Y J. The determination of the most probale mechanism function and three kinetic parameters of exothermic decomposition reaction of energetic materials by a single non-isothermal DSC curve[J].Thermochim Acta.，1988，123：135-151.

[8] Zsako J. Kinetic Analysis of Thermogravimetric data[J].J Phys Chem.，1968，72（7）：2406-2411.

[9] Kissinger H E. Reaction kinetics in differential thermal analysis [J]. Anal Chem.，1957，29（11）：1702-1706.

[10] Flynn J H，Wall L A. General treatment of the thermogravimetry of polymers[J]. Journal of Research of National Bureau of Standard- A Physical Chemistry，1966，70A：487-523.

[11] Ozawa T. A new method of analyzing thermogravimetric data[J]. Bull Chem Soc Jpn.，1965，38：1881-1886.

[12] Friedman H L. Kinetics of thermal degradation of charforming plastics from thermogravimetry.Applications to a phenol plastic[J].J Polym Sci Polym Symp., 1964；41：183-195.

[13] Coats A W,Redfern J P.Kinetic parameters from thermogravimetric data[J]. Nature, 1964：201：68-69.

[14] Criado J M，Malek J，Ortega A. Applicability of the master plotsin kinetic analysis of non-isothermal data[J].Thermochimica Acta.，1989，147：377-385.

[15] Xiu-Li Wang，Ke-Ke Yang，Yu-Zhong Wang, et al. Thermogravimetric analysis of the decomposition of poly(1,4-dioxan-2-one)/starch blends[J].Polymer Degradation and Stability，2003，81：415-421.