上证指数基于SVD的组合预测模型
刘常明,张德生,李金凤,任世远
(西安理工大学 理学院, 陕西 西安 710054)
0 引 言
对于股票投资者来说,获得高额的投资收益一直是他们追求的目标,如果能对股价进行准确的预测,就可以避开市场风险,同时,政府部门也可以对股票市场进行有效的监管.因此,对股票市场进行建模预测研究,对于经济和金融市场的发展具有非常重要的意义.然而,股票市场受到诸如国家政策、国际环境、经济形势、政局形势以及投资者心理等许多因素的影响[1],具有高度的不确定性和高噪声等特点.因此,在对股价进行建模预测分析时,有必要将噪声部分从原始序列中分离出来进行研究,对趋势部分建立BP神经网络模型;对随机部分建立ARMA-GARCH模型,这样可以充分发挥各自的优点.
1 奇异值分解(SVD)滤波算法[2]
对于零均值化的序列S={S1,S2,…,Sn},奇异值分解(SVD)滤波的步骤如下:
(1) 构造矩阵
(1)
其中,h=[(n+1)/2],[·] 表示取整数,N=n-h+1.
(2) 对∏进行奇异值分解
∏=UΓVT
(2)
其中,U、V分别是N×N和h×h正交矩阵.
(3)
其中,Δq×q=diag(δ1,δ2,…,δq),δi(i=1,2,…,q),称∏为矩阵的奇异值,且δ1≥δ2≥…≥δq,q≤min(N,h) ,是矩阵∏的秩,若∏列满秩,则h=q.
(3) 门限控制
设定门限值η(0<η<1),解关于r的方程:
(4)
得到正整数r,将其余q-r个奇异值置为0,得到:
(5)
其中,Δr×r=diag(δ1,δ2,…,δr) .
(4) 重构序列
重构矩阵:
(6)
对∏′中下标相同的元素求平均得到趋势序列S′={S1′,S2′,…,Sn′},噪声序列为S-S′.
2 BP神经网络与ARMA-GARCH模型
2.1 BP神经网络
BP神经网络是目前最成熟、应用最广泛的神经网络,它是多层非线性映射网络,采用最小误差学习方式[3].在学习的过程中实现输入模式与输出模式之间的非线性映射.BP神经网络是前馈神经网络,由输入层、隐层和输出层组成,层内之间没有信息的传递,前一层的输出是下一层的输入,在学习过程中不断调节网络的连接权,使得最小均方误差达到所设定的要求,典型的BP神经网络结构如图1所示.

图1 BP神经网络模型
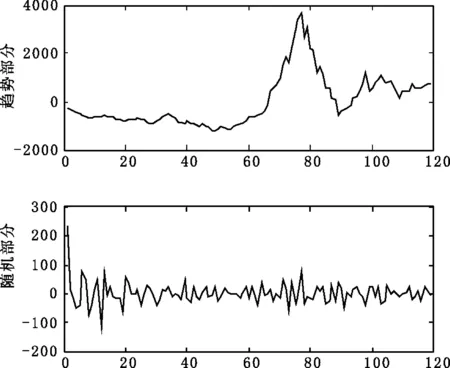
图2 奇民值分解
2.2 ARMA-GARCH模型
回归模型中一个重要假设就是残差是同方差的,它保证了回归系数估计的无偏性、有效性与一致性.当回归模型的残差是异方差时,回归系数的估计就不再是有效的和一致的.金融时间序列大多具有“尖峰厚尾”和波动聚集性等特征,针对这一特征,美国经济学家RobertF.Engle[4]于1982年提出了ARCH模型,BollerSlev[5]于1986年将此模型发展为广义条件异方差(GARCH)模型,它们很好的描述了金融时间序列的波动特征.ARMA-GARCH模型的一般形式为:
(7)
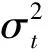
3 上证指数的BP神经网络与ARMA-GARCH的组合预测模型
3.1 奇异值分解
本文以2001年6月到2011年4月的上证月度收盘指数为研究对象,前114个数据作为模型拟合样本,后5个数据作为预测样本,用来检验模型的预测效果.
在对上证指数进行奇异值分解之前需要确定门限控制的大小,确定门限的原则是:
(1) 保证所分离出来的噪声部分是平稳序列,这是因为对噪声部分建立ARMA-GARCH模型的前提是序列是平稳的.
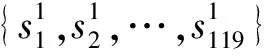
3.2 趋势部分的拟合、预测
在进行网络训练时,为了避免由于净输入绝对值过大使得神经元的输出进入饱和区[6],导致网络的训练速度过慢,对数据进行归一化处理,使其变换到[0,1]范围内,经过多次试验后,最终建立了网络结构,拟合、预测效果如图3和表2所示.
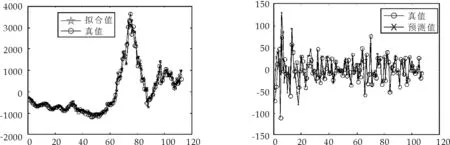
图3 趋势部分拟合图 图4 随机部分拟合图
3.3 随机部分的拟合、预测
3.3.1 模型识别和参数估计
从表1可以看出,序列的偏相关系数在6处截尾,因此初步认为应该建立AR(6)模型.
表1序列自相关系数和偏相关系数

经过系数的显著性检验以及AIC最小准则,最后确定模型为AR(6)模型,应用最小二乘估计法进行参数估计,利用Eviews得到AR(6)的模型表达式为:
y1=-0.838 129yt-1-0.994 258yt-2-0.824 585yt-3-0.841 608yt-4-0.530 638yt-5-0.379 207yt-6
3.3.2 ARCH检验
金融时间序列常常出现异方差现象,异方差会导致回归系数的估计不是有效的与一致的,因此有必要对残差进行异方差检验,我们对残差的平方序列进行相关性检验,显著性水平0.05下的x2统计量的临界值为23.209 3,x2统计量的值为20.804 7<23.209 3,故认为残差平方序列是相关序列,存在异方差性.建立ARMA-GARCH模型为:
均值方程:
拟合、预测效果如图4和表2所示.
3.4 上证指数的预测
将趋势部分的预测值与随机部分的预测值叠加,得到上证指数的预测值如表2和图5所示.

表2 实际值与预测值对比
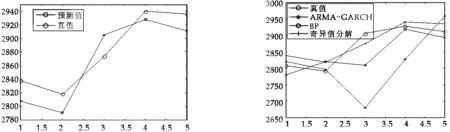
图5 预测效果图 图6 模型预测效果对比
3.5 预测效果比较
为了检验本文所建模型的好坏,对上证指数分别单独建立BP神经网络模型和ARMA-GARCH模型并进行预测,这里只给出预测结果,并与本文所建组合模型的预测结果进行比较,结果如图6所示.3个模型预测结果的MAE与MSE对比如表3所示.

表3 三个模型的MAE、MSE对比
从图6可以看出,基于SVD的组合模型预测精度较高,基本上和实际值的变化趋势是一致的,BP神经网络模型的预测效果也优于ARMA-GARCH模型,这也充分体现了神经网络模型在处理具有非线性特征序列的优势.从表3中也得到了同样的结果.
4 结束语
本文针对股票指数时间序列的非线性和高噪声等特点,通过奇异值分解(SVD)将原序列的趋势部分和噪声部分分离,分别进行研究,建立了上证指数的基于SVD的组合预测模型,取得了较好的预测效果,该模型一方面避免了将趋势部分和噪声部分混为一谈导致的单模型预测精度偏低;另一方面充分利用了BP神经网络的非线性映射能力.同时,用去掉一部分噪声后的平滑序列训练网络避免了过拟合,进而提高了网络的泛化能力,使其描述数据的非线性关系更加真实.另外,对于随机噪声部分并没有被扔掉,而是建立ARMA-GARCH模型,这样更加符合实际情况,更具有实际意义.
参考文献
[1] 李文静,张德生, 等. 股票价格及其影响因素的灰典型相关分析[J].长江大学学报,2010,7(1):148-150.
[2] 吕永乐,郎荣玲,梁家城.基于信噪比经验值的奇异值分解滤波的门限确定[J].计算机应用研究,2009,26(9):3 253-3 255.
[3] 甘晰艳,张钰玲,等.基于股价预测的仿真研究[J].计算机仿真,2010,27(10):297-300.
[4] Engle Robert. Autoregressive conditional heteroskedasticity with estimate of the variance of U.K. inflation[J]. Econometrica, 1982, 50:987-1 008.
[5] T.Bollerslev. Generalized autoregressive conditional heteroskedasticity[J].Journal of Econometrics,1986,31:3 097-3 327.
[6] 韩力群.人工神经网络教程[M]. 北京:北京邮电大学出版社,2006.

