我国上市商业银行风险溢出效应的测度及分析研究
——基于CoVar模型的分析
李玉贤
(上海交通大学 安泰经济与管理学院, 上海 200035)
0 引 言
金融危机的出现往往是由单一金融机构或经济体的风险引发进而影响整个金融系统而爆发的.随着经济全球化的加快,各金融机构和经济体之间的联系更为紧密,2007年爆发的次贷危机和2011年以来爆发的欧债危机,都是由单一金融机构或经济体引发的金融市场风险迅速扩散到其他国家和地区,最终导致席卷全球的经济危机.然而,现有对金融风险的评估缺乏对市场极端条件下金融机构或经济体之间可能存在的风险溢出效应的估量,可能会导致各金融市场风险水平被严重低估.2008年,Adian和Brunnermeier提出了条件风险价值(CoVar)方法,旨在测量单体金融机构(或金融市场)陷入困境时,其它金融机构(或金融市场)遭受损失的风险[1].与传统的风险计量技术相比,CoVar可以捕捉到金融机构的风险对其它金融机构的溢出效应;从统计技术而言,CoVar从全局性的角度来测量金融机构或经济体间的风险溢出效应,是一种更为全面的测量方法.
金融危机中,大部分金融机构都难以幸免.随着经济全球化,经济金融相互依存度越来越高,金融体系的稳健运行与经济体系长期稳定较快发展紧密相关.Adrian和Shin(2008)利用单个金融市场和单个金融机构的历史数据、借助VaR方法分析了金融体系里连锁的资产负债表的风险溢出效应.Engle和Manganelli(2004)采用分位数回归提出了CAViaR方法.基于Engle和Manganelli对CAViaR的研究,结合学术界对分位数的已有研究,学术界发展出了CoVar来计量和分析金融机构间的风险溢出效应[2].上述研究都为CoVar方法的提出奠定了基础.国内关于溢出效应的研究最早可追溯到2003年.赵留彦、王一鸣(2003)利用向量GARCH模型对我国A、B股进行实证检验,研究表明存在A股向B股的单向溢出效应,这种溢出效应在2001年B股对境内投资者开放后得到加强[3].张瑞锋(2006)克服了以往溢出效应研究的缺陷,实证考察了多个金融市场对一个金融市场的协同波动效应.研究结果显示,考虑多个金融市场对一个市场的协同波动溢出更合理有效,与实际更相符[4].
1 模型相关方法介绍
1.1 条件风险价值CoVar相关介绍
1.1.1 条件风险价值CoVar理论
JP.Morgan在20世纪90年代提出的VaR(Value at Risk)对风险测度理论与实践产生了革命性的影响,已经成为风险管理领域的主流技术,广泛应用于各大金融机构和金融监管部门.然而,随着风险管理实践的深入,人们逐渐发现VaR本身存在一定的局限性,其最大的不足在于它只能估计正常市场条件下资产组合的潜在风险,并没有涵盖极端性的市场条件,这使得VaR技术在金融危机时期显得特别脆弱.Adrian和Brunnermeier(2008)在VaR的基础上提出一个测量金融机构之间风险溢出的方法——CoVar.CoVar被定义为当特定金融机构陷入困境时其他金融机构的VaR,一般而言,VaR和CoVar之间的差别体现在CoVar可以捕捉到其他金融机构的风险对某金融机构的溢出效应[5].
1.1.2 CoVar的定义
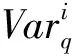
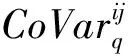



1.2 分位数回归方法(Quantile Regression 简称QR)
1.2.1 分位数回归方法在风险价值方面的应用综述
众所周知,传统的线性回归方法描述了因变量均值受其他因素影响的情况,且利用普通最小二乘法(OLS)估计出来的参数具有最优线性无偏性.然而现实中的金融数据往往服从尖峰厚尾分布且存在显著的异方差,这会导致普通最小二乘法的失效.同时,普通最小二乘法只描述了总体的平均信息,不能充分体现因变量分布各部分的信息.为了弥补传统线性回归方法的不足,Koenker和Bassett(1978)首先提出了分位数回归的思想,分位数回归根据因变量的条件分位数对自变量进行回归,可以得到所有分位数下的回归模型[6].因此,分位数回归能够更全面反映部分因变量受自变量的影响情况.
1.2.2 分位数回归的基本思想和系数估计
假设随机变量X的分布函数如下:
F(x)=Pr(X≤x)
Y的q分位数Q(q)定义为满足F(x)≥q的最小y值,即:
Q(q)=inf{x∶F(x)≥q}, 0 其中,中位数可以表示为q(0.5),对于Y(y1,y2,…,yn) 的一组随机样本,样本均值回归是使误差平方和最小,即: 样本中位数回归是使误差绝对值之和最小,即: 一般的样本分位数回归是使加权误差绝对值之和最小,即: 对于回归方程 Yi=α+βXi+εi,i=1,2,…,n 若使用QR方法对回归方程进行估计,我们记分位点函数为: Q(q|Xi)=α+βXi 在使用QR方法对参数α和β进行估计时,我们一般通过求解下式得到: 从上式容易看到,通过改变q就可以得到不同的分位数回归曲线(由α和β的不同估计值代表).q反映了因变量Y的不同水平,在金融风险实践中我们可以通过选取较小的q值(如q=0.05)来考察收益率左尾(代表损失)受其他因素影响的情况.分位数回归技术为我们全面理解金融风险提供了全新的方法和思路.由于VaR 本质上就是一个分位数,而CoVar本身又是VaR,所以CoVar也是一个分位数,可以通过建立分位数回归来对CoVar进行有效分析. 截至2011年9月30日,我国上市商业银行共有16家,根据对上市商业银行的研究,在研究对象的首发上市时间上,农业银行和光大银行都是于2010年7月以后在上海证券交易所和香港证券交易所上市交易,交易时间过短;且农业银行和光大银行上市流通股占总股本比例分别只有15.76%和35.73%,流通股比例过低,未能反映公司交易所市场整体表现,因此在研究对象里剔除上述两家银行.可以发现其余14只银行股上市时间均在2007年10月1日之后,距离目前已经超过四年,数据量足够进行分析;且上述14只银行股上市流通股占总股本比例均超过60%,流通股所占比例较高,公司股价变动能够反映公司在资本市场的整体表现.因此,选取这14只银行股作为本文的研究对象. 2.2.1 数据选择方法及相关解释 (1)本次银行股整体指数和收益率计算以2007年10月8日为起始日,以2011年9月23日为结束日,采用前复权方式,共可获得965个交易日数据.在此周期内,曾经历了美国次贷危机及欧洲债务危机为主的全球新一轮金融危机,因此,此时间段内的银行股价格水平具有很强的参考意义. (2)由于银行股票市场的风险传导需要一定的时滞,本文选用周数据进行实证分析.故选取每周末股价收盘价数据,一共可以获得193个周数据. (3)对于只在上海证券交易所或只在深圳证券交易所上市的银行股,其银行股价格指数计算以2007年10月12日星期五为基准指数1 000.00点,之后各周指数根据基准指数直接计算. (4)对于在上海(深圳)证券交易所和香港证券交易所都上市的银行股,其银行股价格指数以2007年10月12日星期五为基准指数1 000.00点,之后各周指数以各股指数根据基准指数以每周五收盘价计算的流通股股票市值除以整体流通股股本,港股市值根据每周末的人民币港币汇率计算,如果当天汇率值不存在,则以可获得的上一有效汇率值计算. (5)对于银行股整体指数,与(3)中计算方法类似,其价格指数也以2007年10月12日星期五为基准指数1 000.00点,之后各周指数以作为研究对象的所有14只银行股市值之和除以整体流通股股本,股市值根据每周五的人民币港币汇率计算,如果当天汇率值不存在,则以可获得的上一有效汇率值计算. (6)银行股整体收益率和个股收益率对每个周历史数据取对数一阶差分计算出每个周收益率.为了减少计算误差,我们将所有计算结果乘以100,即: Rt=ln(第t周价格指数/第t-1周价格指数) (7)股价数据及人民币港币汇率数据来源均为wind资讯. 2.2.2 银行股整体指数、收益率的计算及单只银行股指数、收益率计算 我们对银行股指数收益率的均值(Mean)、偏度(Skewness)和峰度(Kurtosis)进行了计算,并对各收益率序列进行了Jarque-Bera检验,偏度(Skewness)、峰度(Kurtosis)和Jarque-Bera统计检验量的计算公式如下所示: 其中S为偏度,K为峰度,J-BJarque-Bera统计检验量,检验数据如表1所示. 表1 各银行股收益率序列统计分析表 根据表1所示,各银行股收益率均呈现左偏,绝大多数银行股收益率峰度K>3,序列分布的尾部比正态分布的尾部厚,其分布呈现出“高瘦”形状,即“尖峰”,符合大多数金融事件序列“尖峰厚尾,非对称分布”的特征. 2.2.3 银行股与银行指数的双向风险溢出效应计算——以深发展为例 根据2.2.2中计算所得的各银行股收益率序列数据,取q=0.05,即求置信度为95%时的风险溢出效应.以深发展为例,建立以下q分位数回归模型,其中sfz代表深发展,yhzs代表银行指数: (-9.580 03) (5.871 827) (-6.139 46) (6.420 764) 根据上式,我们可以最终得到: 类似的,我们可以通过以上方法,得到: 这种做法的优点能更为准确的反映深发展与银行股价格指数间的风险溢出程度,代入之前所算出的数据,深发展与银行股指数之间的相互风险溢出效应数值如表2所示. 表2 深发展与银行股指数之间的相互风险溢出效应数值表 由表2可以发现: (1)使用Var方法测量金融风险都要小于使用CoVar方法所测量的风险,说明使用Var方法对风险的估计过小,尤其是在极端情况下对风险估计的不足. (2)通过对风险溢出效应进行标准化,可以发现当银行业整体发生极端情况时深发展对整个银行业的溢出效应要大大强于深发展发生极端情况时对银行业整体风险的溢出效应,这也与深发展在整体银行业中的地位特征是相符合的. 综上所述,深发展与整体银行股之间存在着双向的风险溢出效应,整体银行股对深发展的风险溢出效应要远强于深发展对整体银行股的风险溢出效应.在风险溢出方向上,二者之间的风险溢出效应都是正向的.以上数据符合我们对中国银行业的一般判断.CoVar将风险溢出效应转化为具体数字,具有很强的操作性,金融机构和监管部门可以借助CoVar来评估其他金融机构(或金融市场)发生风险事件时对本金融机构(或金融市场)的溢出影响程度,提高决策准确性,降低决策风险. 与深发展的风险溢出效应方法类似,我们对各支银行股收益率进行了分位数回归即风险溢出效应的测量,得到以下图形,用来分析风险溢出效应. 2.3.1 当银行业陷入困境时,各银行股总风险价值 图1 当银行业陷入困境时,各银行股总风险价值 图2 当银行业陷入困境时,各银行股风险溢出价值 便于分析,我们在图1中加入一条趋势线,在趋势线上方的银行如中国银行、工商银行和交通银行,其总风险价值水平较低;而在趋势线下方的兴业银行、华夏银行等其风险水平较高.根据资料可以发现资产规模大的银行在银行业陷入困境时,抵御风险能力较强.因此,得到结论1如下: 资产规模大、利润水平高的银行股整体风险溢出效应较低,抗风险能力较强. 2.3.2 当银行业陷入困境时,各银行股风险溢出价值 便于分析,我们同样在图2中加入一条趋势线,在趋势线上方的银行如中国银行、工商银行、交通银行、民生银行和宁波银行,其风险溢出价值较低;而在趋势线下方的兴业银行、招商银行、中信等其风险溢出价值较高.根据资料可以发现不仅资产规模大的银行在银行业陷入困境时,抵御风险能力较强,还可以发现一些区域性商业银行如宁波银行和民生银行,虽然整体风险水平较高,但其风险溢出价值较低,说明在抵御极端方面也具有较强的实力.因此,得出结论2和结论3如下: 图3 当各只银行股陷入困境时,对整体银行业的风险溢出价值 资产规模大、利润水平高的银行股在抵御银行业整体风险溢出效应上能力较强. 部分经营方式灵活、在区域市场具有较强竞争力的银行在抵御银行业整体风险溢出效应上能力强于部分全国性商业银行. 2.3.3 当各只银行股陷入困境时,对整体银行业的风险溢出价值 便于分析,我们同样在图3中加入一条趋势线,在趋势线下方的银行如招商银行、中国银行、中信银行和建设银行等,当各只银行股陷入困境时,对整体银行业的风险溢出价值较高,而上述银行都是资产规模较大的全国性商业银行,因此产生以上效果也符合我们对中国银行业的一般判断.因此,可以得出结论4如下: 资产规模较大的银行股对银行业的整体风险溢出效应较大. 对于金融监管部门而言,CoVar能够用来捕捉单个金融机构发生风险事件时对整个金融体系的溢出效应.这使得金融监管不再拘泥于单个金融机构的风险监管,而是着眼于整个金融体系潜在的风险变化.本文利用分位数回归法和我国已上市银行的收益率序列,测度了我国上市银行业各银行股之间的CoVar,以测量银行业之间的风险溢出效应. 本文得出的结论与国内银行的一般事实相符,为银行业监管部门对银行部门进行监督和管理提供有效参考.金融监管部门可以根据各金融机构对系统风险的贡献度进行有区别的管理, 对风险溢出值较高的金融机构实施更为严厉的监管,确保整个金融体系的稳定,从而抑制金融危机时的金融风险的扩散蔓延. 参考文献 [1] Adrian,Brunnermeier. “CoVar”[R]. Federal Reserve Bank of New York Staff Reports,2008,9. [2] 毛 菁, 罗 猛.银行业与证券业间风险外溢效应研究——基于CoVar模型的分析[J].New Finance, 2011, (05): 27-31. [3] 赵留彦, 王一鸣.AB股之间的信息流动与波动溢出[J].金融研究, 2003,(10): 37-52. [4] 张瑞锋.金融市场协同波动溢出分析及实证研究[J].数量经济技术经济研究, 2006, (10): 141-149. [5] Adrian,Brunnermeier.“CoVar”[R].Federal Reserve Bank of New York Staff Reports,2008,9. [6] 谭治国, 蔡乙萍.分位数回归在风险管理中的应用[J].统计与决策, 2006, (17): 23-24.2 应用CoVar方法对我国上市商业银行风险溢出效应进行实证分析
2.1 研究对象选择
2.2 实证研究过程

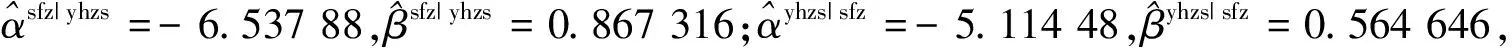


2.3 银行股风险溢出效应实证结果分析


3 结束语

