拉格朗日中值定理证明方法探讨及其推广

张德江

（盐城生物工程高等学校电子工程系，江苏盐城 224051）

拉格朗日中值定理证明方法探讨及其推广

张德江

（盐城生物工程高等学校电子工程系，江苏盐城 224051）

用多种方法证明了拉格朗日中值定理，并对拉格朗日微分中值定理进行了推广.

拉格朗日中值定理；推广定理；证明方法

在数学分析中，微分中值定理占有很重要的地位，因为微积分的许多命题和不等式的证明都是以它为依据，在证明有关中值问题时具有非常重要的作用.本文用多种方法证明了拉格朗日中值定理，并对拉格朗日微分中值定理进行了推广.

1 拉格朗日中值定理及其证明

1.1 拉格朗日中值定理[1-3]

定理1设函数f满足条件（1）f在闭区间[a,b]上连续；（2）f在开区间(a,b)内可导，则在(a,b)内至少存在一点ξ，使得：

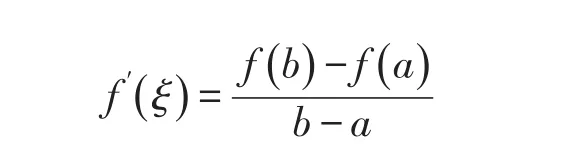
1.2 证明方法探讨

人们对微分中值定理证明方法的研究，经历了从特殊到一般，从直观到抽象，从强条件到弱条件的发展阶段，逐渐认识到微分中值定理的普遍性.对拉格朗日微分中值定理的证明，除数学分析或者高等数学课本上证明方法之外，还有很多值得学习借鉴的方法，本节对两种典型的证明方法进行了总结.

（1）构造函数法[4-5]

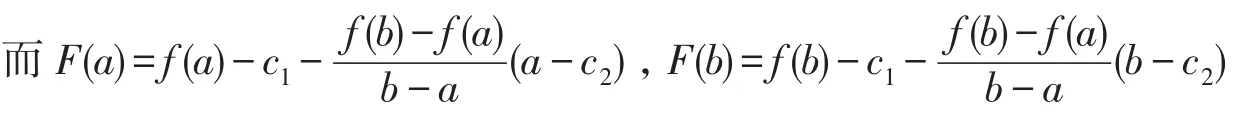
将F(a)与F(b)作差化简得F(a)=F(b).

于是F(x)满足罗尔中值定理的条件，则至少存在一点ξ∈(a,b)，使得

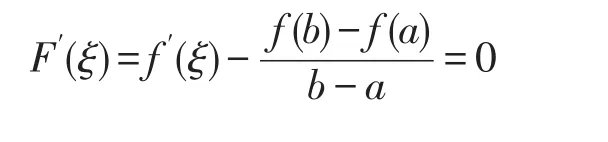
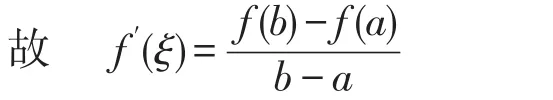
证法二构造行列式型辅助函数

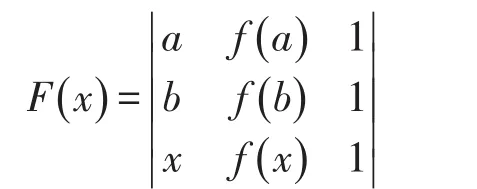
由于f(x)在[a,b]上连续，在(a,b)内可导，所以F(x)为[a,b]上的连续函数，且在(a,b)内可导，且F(a)=F(b)=0，根据罗尔中值定理，至少存在一点ξ∈(a,b)，使得

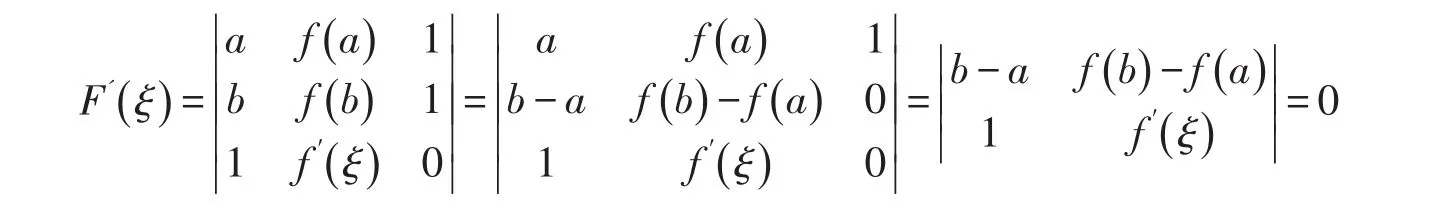
则有f′(ξ)(b-a)=f(b)-f(a)

所以

（2）运用区间套定理证明

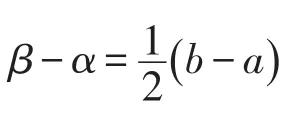
2 推广形式的拉格朗日中值定理及其证明

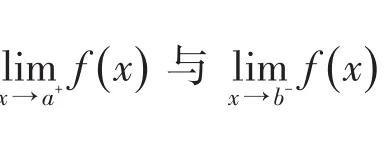
a,b内至少存在一点ξ，使得

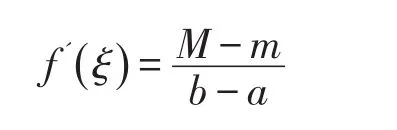
证明首先给出一个引理[7-9]：

则易知函数F(x)在[a，b]上连续，在（a，b）内可导且F(a)=F(b).由罗尔中值定理可知，在（a，b）内至少存在一点θ，使得=0，而在（a，b）内有

根据定理2及其证明过程[10]，我们很容易得到如下推论：

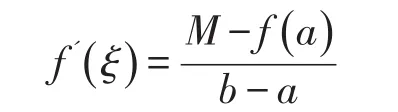
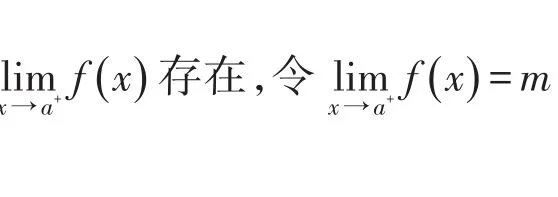
[1]华东师范大学数学系.数学分析[M].2版.北京：高等教育出版社，2001：6.

[2]同济大学应用数学系.高等数学[M].北京：高等教育出版社，2002.

[3]杨耕文.用行列式法证明微分中值定理[J].洛阳大学学报，2006，12：49-52.

[4]张则增，周相泉，王娥.微分中值定理的推广[J].山东师大学报（自然科学版），1998，13（3）：323-325.

[5]游兆永.高等数学解题方法和技巧[M].西安：陕西科学技术出版社，1981.

[6]张弘.微分中值定理的又一证明方法[J].重庆交通学院学报，2004（23）：129-130.

[7]侯谦民.中值定理的推广[J].武汉职业技术学院学报，2003（6）：81-82.

[8]胡付高.微分中值定理的推广及其应用[J].孝感学院学报（自然科学版），2000（04）：16-18.

[9]宋基华，彭鑫根.微分中值定理的一种证明方法[J].北京石油化工学院学报，1995（6）：26-28.

[10]童子双，杨志芳.Lagrange微分中值定理的分析证明法[J].金华职业技术学院学报，2003（3）：56-57.

A Discussion of the Method of Proving Lagrange Mean Value Theorem and Its Generalization

ZHANG De-jiang
(Department of Electronic Engineering,Yancheng Higher Vocational School of Biological Engineering,Yancheng 224051,China)

The differential mean value theorem is the fundamental theorem of differential calculus.It not only connects relationship on the function and derivative,but it is also the cornerstone and the bridge of the differential theory application.In this paper,a variety of methods are used to prove Lagrange's theorem,and give the generalization theorem of the Lagrange differential mean value theorem.

Lagrange mean value theorem;generalization theorem;method of proof

O17

A

1008-2794（2012）10-0041-04

2012-09-03

张德江（1966—），男，江苏盐城人，讲师，硕士，研究方向：导数与积分.