《几个常用函数的导数》教学实录及反思
■武汉市郭希连名师工作室骆惠
《几个常用函数的导数》教学实录及反思
■武汉市郭希连名师工作室骆惠
第一部分教学过程简录
一、创设情境,明确目标
前面我们学习了导数的几何意义是曲线上某点处切线的斜率,切线问题是微分学的中心问题,曲线的切线问题又是我们学习导数应用的一个热点问题。请看下面问题:
教师:确定一条直线需要两个条件,从题中可以分析得切线哪两个条件呢?
学生:易知点P(1,1)即为切点,又由导数的几何意义可得切线的斜率k=f'(1)。
教师:函数在某点处的导数是导函数在该点所对应的函数值,因此解题的关键就在于如何求函数的导数。在导数问题中常常需要求出函数的导数,如何求出函数的导数呢?这节课我们就来研究几个常用函数的导数。
二、合作探究,研究新知
1.例题导析
教师:事实上,导数定义本身,就给出了求导数的最基本的方法,瞬时变化率就是导数,求函数y=f(x)的导数就是求出Δx当趋近于0时,所趋近于的那个值。
(师生共同完成下面求导过程,并强化学生对导数里的概念符号的熟悉和运用)

提炼方法:由导数定义求导数的方法。
教师:下面大家利用所得函数的导数求出前面曲线的切线方程。
教师:求出函数的导数往往是解决导数问题的必经之路,虽然导数定义本身,给出了求导数的最基本的方法,但由于直接运用定义求导数这在运算上很麻烦,有时甚至很困难,我们需要知道一些常用的函数的导数,以方便导数的运算。下面再来求几个常用函数的导数。
2.试一试:你能求出下列几个常用函数的导数吗?(三个学生演排,仿照前例求导)
(1)函数y=f(x)=c的导数(学生演板过程略);
(2)函数y=f(x)=x的导数(学生演板过程略);
(3)函数y=f(x)=x2的导数(学生演板过程略)。
3.在例题解析中,师生共同重点讨论以下内容,讨论有关方法:
(1)规范的过程(让其他学生上黑板纠错);(2)理解当Δx趋近于0时,为常数时所趋近于的那个值就是本身;
教师:在常函数和一次函数的求导中都出现了平均变化率为常数的情况,怎样理解当Δx趋近于0时,为常数时所趋近于的那个值就是本身呢?平均变化率为常数意味着平均变化率受不受Δx值的影响?
学生:不受影响。
(3)对(2)作变式处理:求函数y=2x,y=3x,y=4x的导数,引伸到函数y=kx (k≠0)的导数(为下面几何意义的探究做好铺垫)。
教师:导数是近代数学中微积分的核心概念之一,它的产生有着深厚的物理背景。这三个常用函数的导数蕴涵着怎样的物理意义呢?
探究物理意义:分析上述三个常用函数的导数的物理意义。
教师:如果我把这三个常用函数都看成是路程关于时间的函数(x是时间,y是路程),它们的物理意义又分别是什么?(复习导数物理意义是运动物体在某一时刻的瞬时速度,学生思考作答)
①y'=0可以解释为某物体每个时刻的瞬时速度始终为0,即物体一直处于静止状态。
②y'=1可以解释为某物体每个时刻的瞬时速度始终为1,即物体在做瞬时速度为1的匀速运动。
③y'=2x可以解释在时刻的瞬时速度为2x,即随时间x的改变物体瞬时速度2x也在随着改变,故物体在做变速运动。

函数y = c y = x y = x2导数y'= 0 y'= 1 y'= 2 x物理意义物体静止匀速运动变速运动
教师:三个常用函数的导数的物理意义分别是运动物体的三种不同运动状态。
探究几何意义:分析常用函数的导数的几何意义。
教师:常用函数的导数中又蕴涵着怎样的几何意义呢?我们先来看课本提出的一个探究问题:
根据导数的定义,y=2x,y=3x,y=4x求函数的导数。并在同一平面直角坐标系中,画出它们的图象。
(1)从图象上看,它们的导数分别表示什么?
(2)这三个函数中,哪一个增加得最快?哪一个增加得最慢?
(3)函数y=kx (k≠0)增(减)的快慢与什么有关?
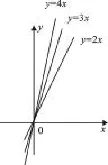
教师:通过前面的学习我们已经得到(1)的答案是什么?
学生:y'=2,y'=3,y'=4导数分别为这些直线的斜率。
教师:很好!(2)联系着(1)进行思考并说明一下为什么。
学生:y=4x增加得最快,y=2x增加得最慢,因为函数y=4x的斜率比函数y=4x的斜率要大。
教师:(3)在(1)(2)的问题上就不难得到答案是什么。
学生:函数增(减)的快慢与斜率k值有关。
教师:由(1)知导数分别表示斜率,而斜率又是导数的几何意义,那不就是函数的增(减)的快慢与其导数有关,它们又有着怎样的关系呢?下面我们进一步来观察一下函数y=x2与函数图象的变化情况与其导数是否存在这种关系。
教师:(打开几何画板)大家带着三个问题观察图像,随着x变大,(1)图像的增(减)变化情况;(2)增(减)的快慢情况(启发:如何看增(减)快慢呢?鼠标像右拖动一格看图像上升下降多少);(3)导数绝对值的变化情况。
1.函数y=x2的导数是y'=2x。(几何图略)
当x>0时y'>0,随着x的增加y'在增大,函数y=x2增加得越来越快。
教师:通过对两个函数图像与导数值的变化情况的观察的结论,我们可以归纳得如下结论:函数图象增(减)的快慢与函数的导数间的关系。
当y'>0时,导数值越大函数增加得越快,导数值越小函数增加得越慢。
教师:此结论说明导数可以反映函数的变化快慢。
教师:下面再来求一个较为复杂点的函数的导数。
(给时间学生在下面求导,稍后师生共同探讨)
教师:求导过程中大家遇到什么难题没有?
教师:你们怎么解决的呢?
有学生抢答:分子实数化。
教师:精彩!分子实数化是无理式常用的变形方法,我们在变中求“通”变中求“活”!
(利用实物投影仪展示学生解答)
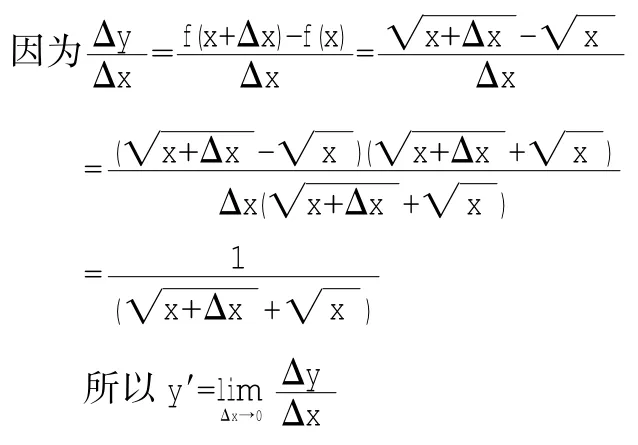
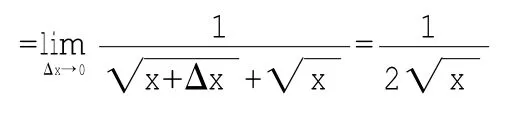
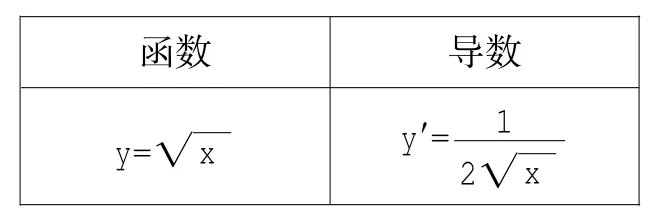
函数导数y=x■y'=1 2x■
探究规律:探究五个函数特点,五个函数与其导数之间的规律。
教师:我们求出了五个常用函数的导数,其实这几个常用函数有一个统一的名称叫幂函数(学生回答)。幂函数的求导有没有统一的规律呢?
教师:请观察,观察结构特征、观察数据特点、观察系数是怎么来的、观察指数是怎么变化的?
学生:导函数的系数是原函数的指数,导函数的指数是原函数的指数减1。
教师:按这个规律我们大胆猜想幂函数y=f(x)=xn(n∈Q*)的导函数是什么?
学生:y'=nxn-1.
推广:若y=f(x)=xn(n∈Q*),则f'(x) =nxn-1
教师:这就是数学所展现出的美与魅力!
教师:它就是下节课中幂函数的导数公式。常用的函数还有很多,如三角函数、指数函数、对数函数。它们的导数都是什么?一个复杂点的函数往往还要进行加减乘除运算,还有复合函数,导数的运算法则又是怎样的.这些我们将在下节课进一步学习。
三、巩固提高
(师生共同探讨,当堂实验以下习题)
1.(1)f(x)=0的导数是()
A.0B.1C.不存在D.不确定

(3).如果函数f(x)=5,则f'(1)=()
A.5B.1C.0D.不存在
四.引导小结
1.用导数定义推导了几种常用函数的导数,它们都是公式要熟记。
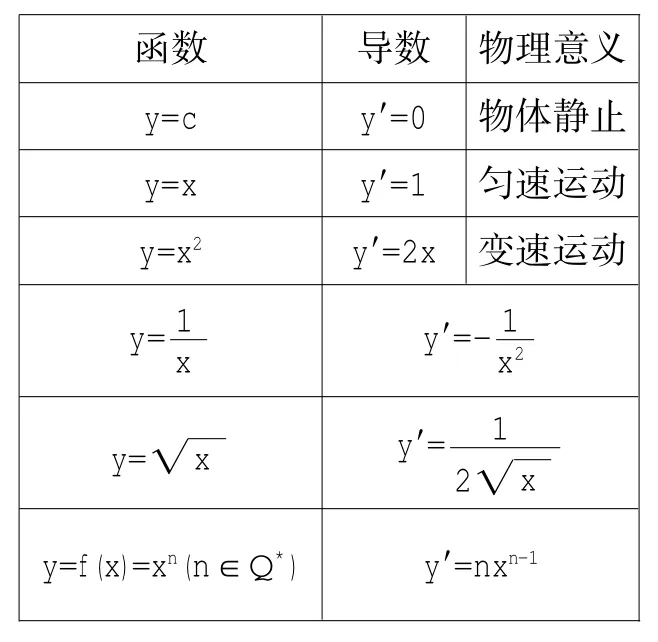
______函数______y=c ______y=x导数_ _ y'=0_ _ y'=1_ _物理意义物体静止匀速运动______y=x_____ __2y'=2x变速运动y=1 ________x y'=-1 x2y=x■y'=1__ _________________ ______2x■y=f(x)=xn(n∈Q*) y'=nxn-1
2.探究了常用涵数导数的几何意义及物理意义。
3.学习了常用函数导数的基本应用,下节课将进一步学习导数的运算及其应用。
五、分层作业
必做题:1.课本18面习题1.2A组第1题;
选做题:(2010·江苏,8)函数y=x2(x>0)的图像在点(ak,ak2)处的切线与x轴的交点的横坐标为ak+1,其中k∈N*,若a1=16,则a1+a2+a3的值是________.
第二部分教学反思
一、基本情况
本节课是我参加武汉市高中数学“课内比教学”的一节参赛课,施教对象为武汉市育才高中平行班学生。由于学生基础不是很好,学生学习导数的知识也才几节课,因此对导数的概念掌握不是很熟练,理解得也不是很透彻,对符号的表示和运用也有些困难,于是教师在教学中就格外注意在探究新知识的同时强化旧知识复习,加深学生对概念的理解,培养学生语言表达及符号运用的能力。
二、教学设计指导思想
本课初看课题感觉本节课内容太单一、太简单,教学中,一般教师不会太重视。通过仔细研读教材、教参,查阅一些资料后,我放弃常规使用的从旧知识的复习入手的方法,改为利用教材中的探究问题即以曲线的切线这个高中导数应用的热点问题引入,首先就让学生明白我们为什么要学习几个常用函数的导数,进一步思考怎样去求函数的导数,而旧知识的复习则采用随着学习的需要逐步进行。
本节课五个常用函数的求导都运用的是导数的定义求导,教学中让学生认识到导数的定义本身就给出了求函数导数最基本的方法,并让学生明确其步骤,本节课的学习又不能仅仅停留在五个常用函数的导数公式的推导上。在教学设计上,教师怎样充分利用五个常用函数的导数来挖掘更深层次的东西,准确表达教材意图,设计了三个探究问题让学生感受导数蕴涵的内涵。一是利用三个函数y=c,y=x,y=x2的导数,让学生感受导数的物理背景;二是利用函数y=x2及函数y=1 x的导数,让学生感受导数中所蕴涵的几何意义;三是利用五个常用函数与其导数间存在的内在规律,让学生感受数学的美与魅力。
最后,让学生在导数问题中感受导数公式给我们带来的便捷,让学生在期盼中去学习下节课更多的导数公式。
(作者单位:武汉市黄陂区第一中学)
责任编辑 王爱民

