Optimization of Fermentation Media for Enhancing Nitrite-oxidizing Activity by Artificial Neural Network Coupling Genetic Algorithm*

LUO Jianfei (罗剑飞), LIN Weitie (林炜铁)**, CAI Xiaolong (蔡小龙) and LI Jingyuan (李敬源)

School of Bioscience and Bioengineering, South China University of Technology, Guangzhou 510006, China

1 INTRODUCTION

Biological nitrification is a key reaction in the global nitrogen cycle [1], whichconvertsammonia to

nitrate in the end ( → →). The process of nitrification involves two important microbial guilds, the ammonia-oxidizing bacteria (AOB) that convert ammonia to nitrite and the nitrite-oxidizing bacteria (NOB) that convert nitrite to nitrate [2]. AOB and NOB are called nitrifying bacteria, which have high activity for degradation of high levels of toxic inorganic nitrogen that is difficult to be assimilated by ecological system itself.

In aquatic ecosystems, high levels of ammonia,nitrite and nitrate are harmful to aquatic animals, and often result in direct (acute or chronic) toxicity [3].Acute toxicity always occurs in salmonids when the concentration of NH3is above 0.2 mg·L-1, so a maximum permissible level of 0.002 mg·L-1NH3is recommended [4]. The main toxic action of nitrite on aquatic animals, particularly on fish and crayfish, is due to the conversion of oxygen-carrying pigments to the forms that are incapable of carrying oxygen, causing hypoxia and ultimately death [5].

We designed a biological technique for enhancing degradation of nitrite in aquaculture wastewater, in which nitrite can be rapidly removed by continually adding NOB with high activity. However, the low yield of energy production pathways and the burden of precursor formation through the incorporation of inorganic carbon led to a slow specific growth rate of NOB [6], resulting in a long culture period. To achieve high activity and reduce the investment costs, it is a prerequisite to design a proper fermentation medium by optimizing.

Many techniques are used to optimize the cultivation medium and product expression, from traditional method of single factor at a time to complex statistical and mathematical approaches, involving experiments with orthogonal array [7, 8], uniform [9],Plackett-Burman [10] and central composite [11] designs, followed by response surface methodology(RSM) [12] and artificial neural networks coupling with genetic algorithms (ANN-GA) [13, 14]. Single factor at a time is the most widely used optimization method, but it is not appropriate for the optimization with more than one factor, because it ignores the interactions among medium components. In the application of RSM in optimization, a model such as full second-order polynomial must be assumed in order to determine the relative influence of each medium component. The number of experiments designed by RSM isLN(Nfactor atLlevels), but in each practice only two or three levels can be applied and the plotting is limited to two variables at a time. Because of the metabolic complexity of microorganisms and usually a large number of variables involved, developing rigorous models to demonstrate the high non-linearity and stability is a critical challenge. Artificial neural networks (ANN) are used commonly as “black box”models of key variables whose relationship to other process entities are neither formally described nor mathematically established, and have been utilized successfully for system design, modeling, optimization and control mainly due to their capacity to learn,filter noisy signals and generalize information through a training procedure [15, 16]. The genetic algorithms(GA) follow the theory of population evolution and base on the principles of “survival-of-the-fittest” and“random exchange of memory during genetic propagation”, which explore large variable spaces to find the specie that fit the best [17]. ANN-GA employs non-linear models to describe the complex interactions and influences among medium components, and bases on a stochastic method for global optimization to reach the optimal medium in a shorter time and a smaller number of experiments.

In this study, BP neural network (BPNN) is applied to construct a non-linear model and used as the objective function of GA to optimize the fermentation medium of nitrite oxidizing bacteria.

2 MATERIALS AND METHODS

2.1 Microorganism

A nitrite degradation strain of NOB-x4 was isolated from an aquarium in Dong Sheng town of Sun Yat-sen city, and identified asNitrobacter winogradskyi(ATCC 25391) according to the American Type Culture Collection. NOB-x4 was maintained in the vapor phase with liquid nitrogen in our laboratory.

2.2 Initial medium and cultivation

The initial medium used for NOB-x4 cultivation was (g·L-1): NaCl 0.3, MgSO4·7H2O 0.14, FeSO4·7H2O 0.03, KH2PO40.136, NaNO20.5, and NaHCO31.6.NaNO2and NaHCO3were the only N source and C source of NOB-x4, respectively, and NaNO2was the only source of energy. NOB-x4 was incubated in 100 ml of medium in 250 ml Erlenmeyer flasks and cultured at 30 °C, initial pH 7.5 on a rotary shaker with rotational speed of 180 r·min-1. After one week of cultivation, the bacterium solution was transferred to a 15 L air-lift bioreactor with fresh medium.

2.3 Analytical methods

Because of the difficulty and long time needed to count the number of NOB in agar plate [18], the optical density at 600 nm (OD600) was introduced as the measurement of the number of NOB in the solution,based on the correspondence of OD600and mixed liquor suspended solids (MLSS) of bacterium solution.The standard curve between OD600and MLSS is

The nitrite oxidization rate (NOR) of NOB serves as a response in this paper. NOR is an index for measuring the capability of NOB degradation of nitrite, which also means the specific activity of nitrite oxidoreductase. Its unit is g2NO--N·(g MLSS)-1·d-1.The NOR is determined by spectrophotometric method (ISO 6777-1984), based on a color reaction.At pH 1.8, a reaction occurs between NO2-N and 4-amimobenzenesulfonamide, generating a diazonium salt, which finally couples withN-(1-naphthyl)-1,2-diaminoethane dihydrochloride and generates a red dye, with a maximum absorption at 520 nm. The absorption values of the red dye at time 0t= and 3t= h are detected to determine the NOR, while NOB is incubated with NaNO2as a substrate [19]. The NOR is calculated as follows

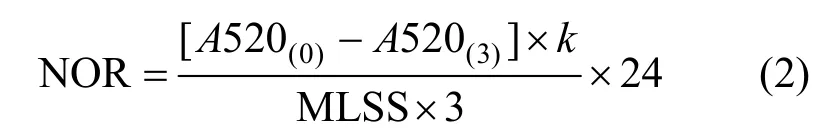
whereA520 is the absorption value at 520 nm, its subscript is the time of detecting,kis the slope of calibration curve of2NO--N, 3 is the time for degrading nitrite, and 24 is the time in one day.

2.4 Experimental method

The minimum and maximum concentrations of each medium component in shake-flask are shown in Table 1. The experiments of optimization were carried out in 250 ml Erlenmeyer flasks with inoculation volume 5 %, and cultured at 30 °C, 180 r·min-1, and pH 7.5.

2.5 Construction of an ANN model

BPNN is introduced in the optimization because it is a widely used ANN and has good ability for nonlinear mapping. BPNN is a neural network that uses the error back-propagation algorithm, whose learning process consists of feed-forward and feedbackward. Each sample signal in feed-forward process is applied by sigmoid functionf(x)=1/(1+e-x) before it passes to the next layer. The situation of neurons on each layer can only affect the situation of neurons on the next layer. If the output layer does not produce the desired value, the errors will be fed back from the outputs to the inputs through the network, and weights of neurons in each layer will be changed along the way. The algorithm repeats in this way until the error values are sufficiently small. The BPNN is trained as shown in Fig. 1.

To predict the NOR of NOB, we use a multi-layer BPNN model composed of input, hidden and output layers (Fig. 2). In the structure of BPNN,the concentrations of six medium components ofNaNO2, KH2PO4, MgSO4, NaCl, NaHCO3and FeSO4are applied as the input vectors to the model, and the NOR of NOB is applied as the output vector. The number of neurons in hidden layer is determined by studying the mean square error (mse) and the iteration times with selected different number of neurons in hidden layer. The mean square error is computed by

Table 1 Medium components and their concentration ranges (g·L-1)

Figure1 Flowchart of BPNN training

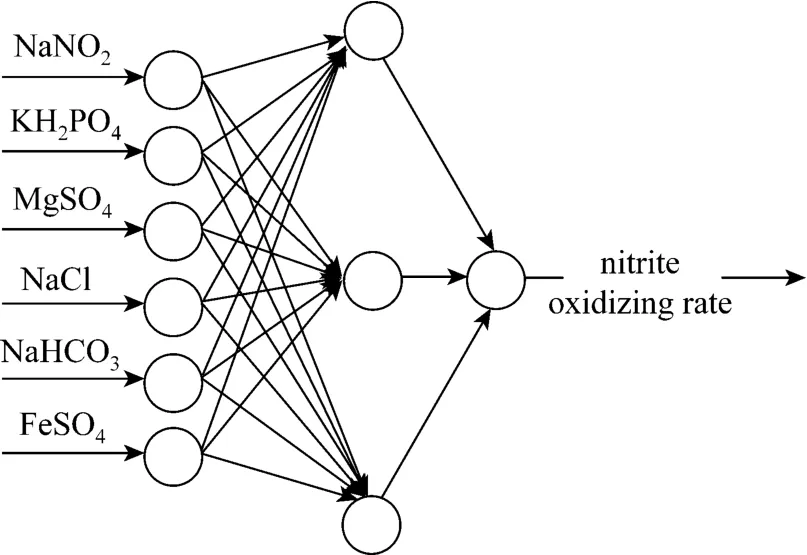
Figure 2 Topological structure of BP neural network(6-13-1)

whereytequals the experimental value at timet, ˆtyequals the estimated value, andnequals the number of experiment.

2.6 Optimization process by GA

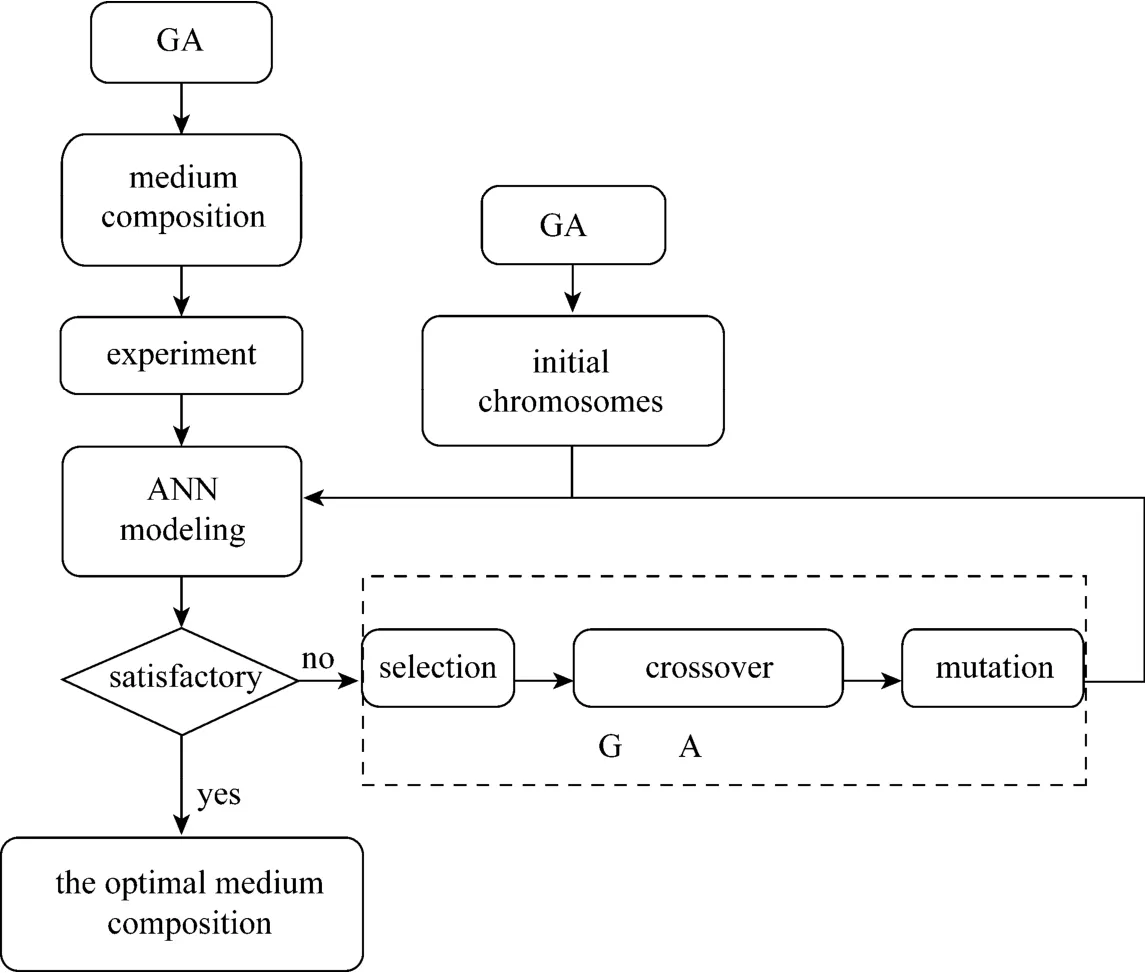
Figure 3 Schema of the working principle for ANN coupling GA

To begin the optimization process of GA, an initial population of candidate solutions is generated,defined as chromosomes. In this paper, the chromosomes consist of six medium components represented by binary strings. After the initial population is generated, the chromosomes are evaluated by an objective function. If the result is not suitable, the process goes to the next step and creates a mating pool using a selection operator. We employ a roulette wheel selection method to select an excellent chromosome in the mating pool. After that, a new population is formed by employing crossover and mutation operators. In the crossover operation, we adopt a single point crossover method: two parent chromosomes are first chosen randomly from the mating pool, then the crossover point in the chromosomes is chosen randomly, and two new chromosomes are finally created by exchanging the excellent genes between the crossover points and the end points of the parent chromosomes. The mutation operation is carried out in such a way that each bit in each chromosome is flipped by a given mutation rate. In addition, we incorporate the elitism strategy into our system. With the selection, crossover,and mutation operations described above, the best chromosomes in the current generation may not be preserved into the next generation. To prevent this situation, the best chromosomes are automatically put in the next generation in the first step. The remaining spots of the next generation are filled by the crossover and the mutation operations. The above procedure is repeated until the predetermined stopping criteria are met or the optimal result is obtained.

In the optimization by ANN coupling GA, BPNN is introduced to obtain a mathematical model to predict the experimental result, and the model is used as the objective function for GA to find the optimal medium composition through the global optimization by GA. The schema of the working principle for ANN coupling GA is shown in Fig. 3.The experiment designed in this paper is generated using the MATLAB©(http:// www.mathworks.com).

2.7 Validation of the optimal medium composition

To validate the performance of the optimal medium optimized by BPNN coupling GA, shake flask validation experiment and scale-up validation experiment were employed. The shake flask experiment was as described in Section 2.4. The scale-up experiment was carried out in a 15 L air-lift bioreactor with a medium volume of 10 L. The culture conditions were controlled at 30 °C, pH 7.5, and dissolved oxygen (DO)2.0-2.5 mg·L-1.

3 RESULTS AND DISCUSSION

3.1 Composition of medium components

Table 2 gives an initial population created with GA as the composition of medium components of experiments. The population is randomly created within the concentration range in Table 1. To evaluate the performance of BPNN, the whole set of experimental results are divided into two groups: a training set and a testing set. The training set is used to build a BPNN model, and the testing set is used to evaluate the model.

3.2 Structure of BPNN

According to the principle of ANN, general nonlinear mapping can be implemented by single hidden layer networks, and the number of neurons in input and output layers bases on the number of input and output vectors. In this paper, there are six input vectors and one output vector, so the number of neurons in input and output layers is six and one, respectively. Selection of the number of neurons for hidden layer is the key to build the structure of ANN. A proper number of neurons in hidden layer can improve the fault tolerance capability, learning rate and generalization ability. Fig. 4 implies that the mean square

error is close to 0 when the number of neurons is more than 8 in the hidden layer. Fig. 5 implies that the number of epochs reduces as the number of neurons increases in the hidden layer, and becomes stable when the number of neurons is more than or equal to 13. Thus 13 neurons are the most proper number for hidden layer. We construct a BPNN whose topological structure is 6-13-1 (Fig. 2).

Table 2 The composition of medium components and the nitrite oxidization rates from experiment,prediction and test by BPNN①

For construction of artificial neural networks, selection of the neurons of layers is crucial. Generally speaking, the numbers of neurons in input and output layers depend upon the number of vectors in input and output. For a selected ANN model, determination of the number of neurons in hidden layer is the most important. The model cannot obtain enough information for the relation between different factors lacking of neurons in the hidden layer, and if the number of neurons in hidden layer is too many, the noise in the training set will be learned by model itself, resulting in over-fitting of the model. Kurkova [20] proved that the number of neurons in hidden layer followed Kolmogorov’s theorem, which is 2n+1, wherenis the number of neurons in input layer. In this paper, we choose 13 as the number of neurons in hidden layer,determined by studying of the mean square error and the iteration times when constructing the BPNN model, according to the Kolmogorov’s theorem.

Figure 4 Mean square error for different number of neurons in the hidden layer with 0.001 as the goal set for BPNN training

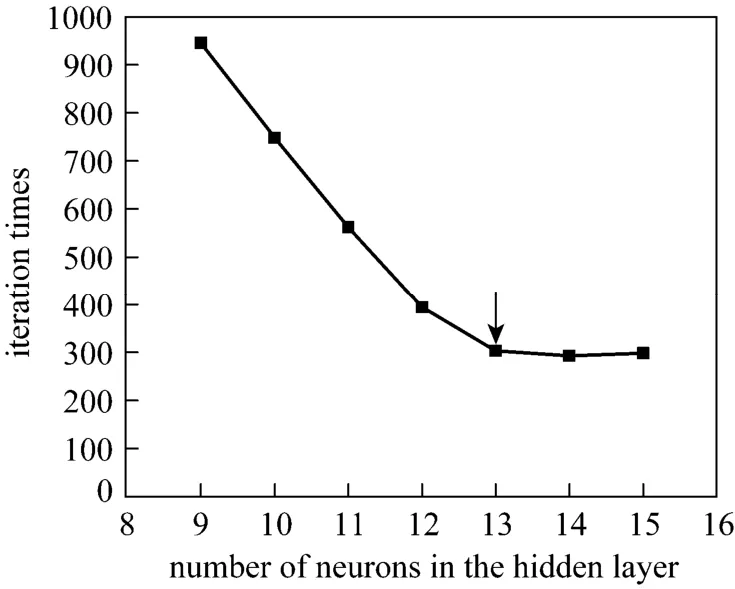
Figure 5 Iteration times for different number of neurons in the hidden layer for BPNN training

3.3 Training and testing of BPNN

Figure 6 shows the parity plot of NOR, constructed with the predicted results of training set and testing set (Table 2). TheR-square of fitting line is 0.95771 and almost all data are in the 95 % confidence limit, which suggests that the BPNN has a good capability to fit the experimental results and is suitable to predict the experimental results.

3.4 Optimization by using BPNN-GA

Figure 6 Training and testing for nitrite oxidization rate(training with 40 randomly selected experiments andtesting with the rest 8 experiments)○ training set; △ testing set; fitting line; 95% confidence limits

An initial population of experiments is created as a starting point for medium optimization. The values of GA-specific parameters used in the optimization simulations are: the length of each medium componentL=20, chromosome lengthl=120, population sizeN=48, ′crossover probabilityp=0.7, mutationprobabilityp=0.05, and the number of generations over which GA evolvesn=500.

The changes of the maximum value and the mean value of population while optimized by BPNN-GA are shown in Fig. 7. The optimal value is found after 50 generations. For an objective function maximization problem, a thorough exploration of the solution space is necessary to secure a solution that corresponds to the local or global maximum [22]. Accordingly, the GA based optimization simulation is repeated by using a different randomly initialized population of the candidate solutions each time, so that different initial populations ensure that each time the GA begins its search for the optimal solution from a different search sub-space, which helps in locating the local or the global maximum on the objective function surface [17].Accordingly, the best solution obtained after 50 iterations of generation is shown in Fig. 7.

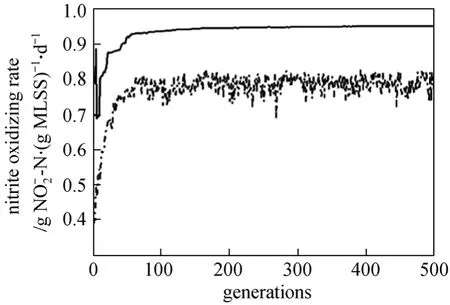
Figure 7 The maximum value and the mean value of population iterating 500 times created by the software of MATLAB change of the maximum value; change of mean value of population

3.5 Validation of the optimal medium composition

After the optimization by BPNN-GA, the optimal cultivation medium was found. To validate the optimal medium, experiments of validation were carried out. In the repeated shake flat experiments, the results of NOR are 0.983, 0.971 and 0.925 g2NO--N·(g MLSS)-1·d-1.One simplettest shows that the experimental results have no significant difference with the optimal result predicted by BPNN-GA. The scale-up experimental result showed that with NOB cultured in the initial medium and in the optimal medium, the nitrite degraded completely at 44 h and 34 h, respectively. It is obvious that the NOB has a higher NOR or higher growth rate when cultured in the optimal medium (Fig. 8), in which the controlled trial indicates that no inoculum with NOB appears in the bioreactor.

4 CONCLUSIONS

A BNPP model was constructed on the basis of the data from 40 experiments, and verified as suitable artificial neural networks for describing complex interactions and influences among different medium components. The model of BPNN with the topological structure of 6-13-1 has a strong learning ability and a

Figure 8 Scale-up experiments when cultured in the initial medium and in the optimum medium (with the inoculums volume of NOB of 5%, about 1.41 g MLSS)■ initial medium; ● optimal medium; ▲ controlledtrial of initial medium; ▼ controlled trial of optimal medium

generalization ability and is able to predict the experimental results effectively. After optimization, the NOR of NOB obtained is 0.952 g2NO--N·(g MLSS)-1·d-1.A scale-up experiment shows that cultured with the medium optimized by BPNN-GA, the time required for complete nitrite degradation by NOB is 10 h less than that cultured with the initial medium. The optimization by using ANN-GA hybrid methodology improves the nitrite oxidization rate considerably. The approach presented in this paper is general and can be employed for modeling and optimization for other microorganism media, even the bioprocesses.

NOMENCLATURE

1 Graham, D.W., Knapp, C.W., van Vleck, E.S., Bloor, K., Lane, T.B.,Graham, C.E., “Experimental demonstration of chaotic instability in biological nitrification”,ISME J., 1, 385-393 (2007).

2 Rittmann, B.E., McCarty, P.L., Environmental Biotechnology: Principles and Applications, McGraw-Hill, New York (2003).

3 Camargo, J.A., Alonso, A., “Ecological and toxicological effects of inorganic nitrogen pollution in aquatic ecosystems: A global assessment”,Environ.Int., 32, 831-849 (2006).

4 Haywood, G.P., “Ammonia toxicity in teleost fish: A review”,Can.Tech.Rep.Fish.Aquat.Sci., 1177, 1-35 (1983).

5 Jensen, F.B., “Nitrite disrupts multiple physiological functions in aquatic animals”,Comp.Biochem.Phys.A, 135, 9-24 (2003).

6 Hagopian, D.S., Riley, J.G., “A closer look at the bacteriology of nitrification”,Aquacult.Eng., 18, 223-244 (1998).

7 Revankar, M.S., Lele, S.S., “Synthetic dye decolorization by white rot fungus, Ganoderma sp WR-1”,Bioresource Technol., 98,775-780 (2007).

8 Silveira, R. G., Kakizono, T., Takemoto, S., Nishio, N., Nagai, S.,“Medium optimization by an orthogonal array design for the growth ofmethanosarcina barkeri”,J.Ferm.Bioeng., 72, 20-25 (1991).

9 Hu, C., Qin, Q., Gao, P., “Medium optimization for improved ethanol production in very high gravity fermentation”,Chin.J.Chem.Eng., 19, 1017-1022 (2011).

10 Li, Y., Liu, Z.Q., Cui, F.J., Liu, Z.H., Zhao, H., “Application of Plackett-Burman experimental design and Doehlert design to evaluate nutritional requirements for xylanase production by Alternaria mali ND-16”,Appl.Microbiol.Biot., 77, 285-291 (2007).

11 Minocha, N., Kaur, P., Satyanarayana, T., Kunze, G., “Acid phosphatase production by recombinantArxula adeninivorans”,Appl.Microbiol.Biot., 76, 387-393 (2007).

12 Guo, J., Luo, Y., Fan, D., Gao, P., Ma, X., Zhu, C., “Analysis of metabolic products by response surface methodology for production of human-like collagen II”,Chin.J.Chem.Eng., 18, 830-836 (2010).

13 Fang, B.S., Chen, H.W., Xie, X.L., Wan, N., Hu, Z.D., “Using genetic algorithms coupling neural networks in a study of xylitol production:Medium optimisation”,Process Biochem., 38, 979-985 (2003).

14 Moreira, G.A., Micheloud, G.A., Beccaria, A.J., Goicoechea, H.C.,“Optimization of the Bacillus thuringiensis var. kurstaki HD-1 delta-endotoxins production by using experimental mixture design and artificial neural networks”,Biochem.Eng.J., 35, 48-55 (2007).

15 Franco-Lara, E., Link, H., Weuster-Botz, D., “Evaluation of artificial neural networks for modelling and optimization of medium composition with a genetic algorithm”,Process Biochem., 41, 2200-2206(2006).

16 Montague, G., Morris, J., “Neural-network contributions in biotechnology”,Trend.Biotech., 12, 312-324 (1994).

17 Desai, K.M., Akolkar, S.K., Badhe, Y.P., Tambe, S.S., Lele, S.S.,“Optimization of fermentation media for exopolysaccharide production from Lactobacillus plantarum using artificial intelligence-based techniques”,Process Biochem., 41, 1842-1848 (2006).

18 Wilen, B.M., Jin, B., Lant, P., “The influence of key chemical constituents in activated sludge on surface and flocculating properties”,Water Res., 37, 2127-2139 (2003).

19 Salem, S., Moussa, M.S., van Loosdrecht, M.C.M., “Determination of the decay rate of nitrifying bacteria”,Biotechnol.Bioeng., 94,252-262 (2006).

20 Kůrková, V., “Kolomogorov’s theorem and multilayer neural networks”,Neural Networks, 5, 501-506 (1992).

21 Ren, J., Lin, W.T., Shen, Y.J., Wang, J.F., Luo, X.C., Xie, M.Q.,“Optimization of fermentation media for nitrite oxidizing bacteria using sequential statistical design”,Bioresource Technol., 99,7923-7927 (2008).

22 Nandi, S., Ghosh, S., Tambe, S.S., Kulkarni, B.D., “Artificial neuralnetwork-assisted stochastic process optimization strategies”,AIChE J., 47, 126-141 (2001).