GMSK调制器在电力线通信中的实现

陈亮 张超 沈兵

（海军工程大学，湖北武汉 430033）

0 引言

电力线通信（Power Line Communication，简称PLC）技术是利用配电网输电线路作为信号的传输信道，使用载波方式传输高速数据、话音、图像等多媒体业务信号的一种通信方式。利用电力线可以传输远程保护信号等数字信息，且电力线机械强度高，可靠性好，作为通信信道不需要额外的线路敷设，因此PLC具有较高的经济性和可靠性，在电力系统控制、继电保护和智能家居中有着广泛的应用前景。但是电力线不同于普通数据通信线路，当其作为数据传输信道时，线路上有许多不可预测的噪声和干扰源，随着负载的投入和切除，电力线特性也在不断的发生变化[2]。因此，电力线通信系统的信息调制技术也日渐成为研究的热点。

近年来，电力线通信系统采用的调制技术主要是 OFDM（正交频分复用）、GMSK及常规的QPSK（相移键控）、FSK（频移键控）等。连续相位调制技术是未来调制解调技术的发展趋势，GMSK就是一种典型的连续相位调制方式。GMSK具有恒包络、相位连续的特点，其已调信号功率谱主瓣窄且带外衰减快，对邻道的干扰小，频谱效率较高[3]。因此GMSK信号在有邻道干扰和非线性功率放大器的系统中具有很好的性能，很适合于电力线信道[2]。工程上GMSK调制器的实现方式很多[5]，包括直接VCO调制法、PLL锁相调制法和波形存储正交调制法。波形存储正交调制法由于易于硬件实现，实际应用较多，但是传统的正交调制法采用的是 DAC之后的模拟信号进行混频，存在I/Q支路信号幅度及正交载波相位的不平衡问题，影响已调信号的性能，而采用全数字的实现方式则可有效地避免这些问题。

本文介绍了GMSK调制的基本原理，分析了传统GMSK调制实现方式的优劣，同时结合工程实际，对波形存储正交调制法的实现结构进行了数字化设计，并在FPGA上加以实现。理论分析和计算机仿真都证明了这种数字实现结构产生的GMSK信号在电力线通信系统传输中具有优良的性能。

1 GMSK调制的基本原理

GMSK信号产生原理如图1。

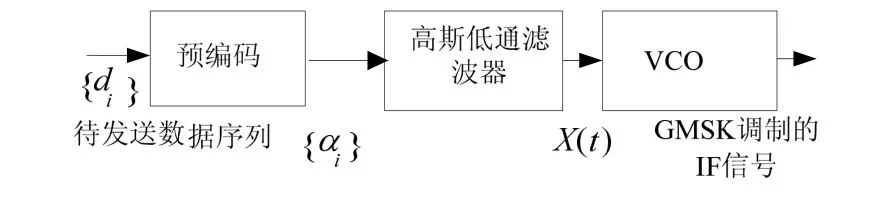
图1 GMSK信号产生原理

高斯滤波器的传输函数和冲激响应分别为

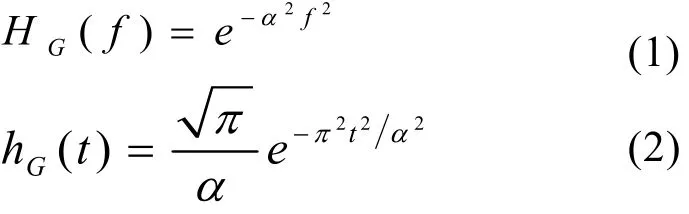
式中，参数α与HG（f）的3 dB基带带宽B有关，即

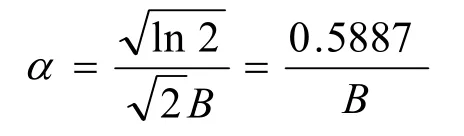
为了方便GMSK的解调，需要对输入数据进行差分预编码。设输入数据为di∈｛0,1｝，将差分编码之后的双极性不归零数据αi通过高斯低通滤波器，则高斯滤波器的输出为

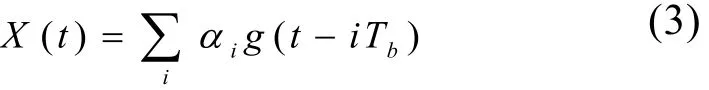
式中Tb为码元周期，g（t）为高斯滤波器的矩形脉冲响应。把X（t）加于 VCO（压控振荡器），经调频后的GMSK信号为

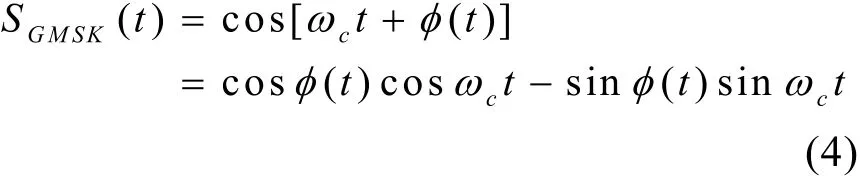
式中ωc为混频频率，相位路径

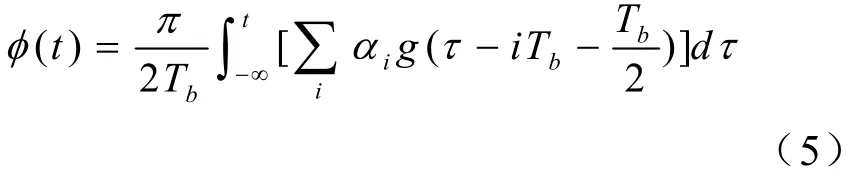
由（4）式可见，GMSK实现时可采用正交相位调制。由于g（t）的取值范围为（-∞,∞），它是物理不可实现的，因此在工程中均需要对g（t）进行截短或近似。

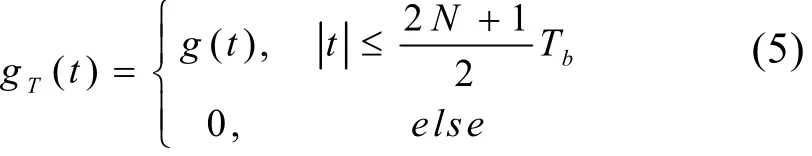
经计算，对于BTb=0.3，当N=2时，有

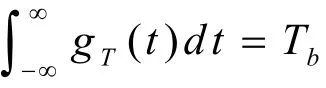
因而，在具体计算Φ（t）时，取g（t）的截短长度为5Tb，具有足够的精度。

2 GMSK调制的硬件实现

2.1 传统的实现方法

在目前的工程应用上，最简单的方法如图 1所示，即用基带高斯脉冲序列直接调制 VCO的频率。这种实现方式的结构简单，但是调制器受VCO频率稳定性的影响大，难以保证GMSK信号的性能。另一种实现方法是采用锁相环的PLL型调制器，如图2所示。锁相技术的采用解决了频率稳定性的问题，但BPSK（二进制相移键控）移相器存在相位突变，为使码元转换点的相位连续且没有尖角，锁相环的传递函数应具有良好的平滑性能和快速响应能力，这增加了硬件实现的复杂程度，因而实际应用有一定局限[7]。

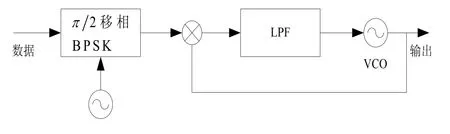
图2 PLL型GMSK调制器

实际应用较多的实现方法是波形存储正交调制法[8]。由公式（4）可知，在计算Ф（t）后，即可算出 GMSK信号。在时刻t，Ф（t）只与输入数据和g（t）有关，而g（t）只取决于其截短长度，因此Ф（t）的状态是有限的，这样由Ф（t）形成的 cosФ（t）和sinФ（t）也只有有限个波形。波形存储正交调制法的基本思想就是将 cosФ（t）和 sinФ（t）离散化，制成表，储存在 ROM中，根据输入的二进制数据查找波形存储表获得基带I/Q信号，再分别经数模变换（DAC）、低通滤波后进行混频。调制器的原理结构如图3所示。这种方法的优点是利用数字技术可以产生具有任何响应特性的基带脉冲波形和已调信号，缺点是两条支路的基带信号的振幅误差以及支路上载波的正交相位误差和幅度误差均会引起已调输出信号的振幅波动和相位误差，即I/Q支路信号幅度及正交载波相位不平衡。在输入数据｛di｝为随机序列的情况下，会导致已调信号包络起伏。限幅前其功率谱不受影响，而限幅后的功率谱有扩展现象[8]。所以，在工程实现上必须尽量避免这一问题。

2.2 全数字实现方法

随着数字器件的发展特别是DDS（数字频率合成）技术的广泛应用，在查找波形存储表获得基带I/Q数字信号以后不经D/A转换而直接进行DDS数字混频，就能避免因为模拟滤波而产生的I/Q支路信号幅度失衡。这样的I/Q数字信号经过低通滤波器（LPF）抑止高频分量后，再通过DDS进行数字混频，就能够得到 GMSK数字已调信号。DDS完全可以保证载波相位的正交性，因此在采样精度允许的范围内，数字化实现GMSK调制器，就能有效避免I/Q两条支路信号幅度及正交载波相位失衡。

FPGA包含丰富的IP core资源，其中就有正弦余弦查找表和 DDS，因此我们在硬件上选择FPGA来全数字实现GMSK调制器，如图4所示。通过将相位路径Ф（t）离散化，存储在图中的相位路径表中，由输入的二进制数据查找相位路径表获得相位路径Ф（t），正弦余弦查找表计算出相应的cosФ（t）及sinФ（t），这样就得到了基带I/Q信号。经过内插并抑止高频分量后，再进行数字混频，最后就能得到GMSK数字已调信号。

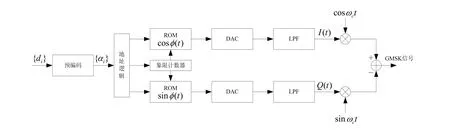
图3 波形存储正交调制法原理框图

图4 基于FPGA的改进实现结构

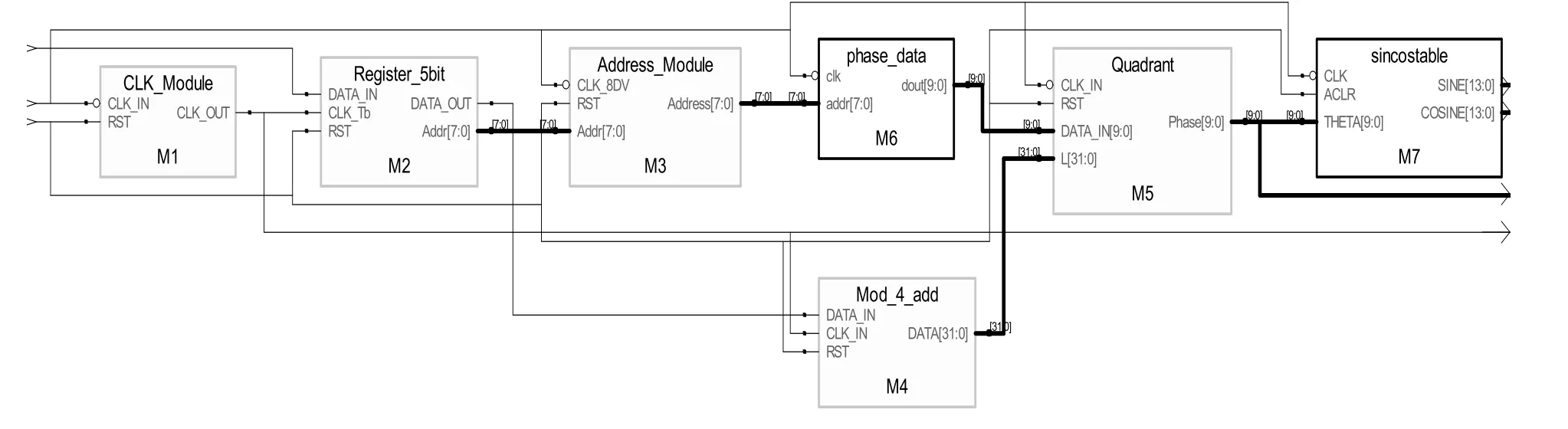
图5 FPGA实现后的顶层RTL原理图

按照图4所示结构实现GMSK数字调制器，我们在Xilinx公司的xc2v6000-4芯片上进行了测试与仿真，测试采用的开发环境为 ISE6.3_01i，综合工具选用 Synplify Pro v7.6，仿真工具为Modelsim 5.8b。选取输入码元序列为二进制贝努利序列，码元宽度为Tb（1/Tb=2.4 kbit/s），g（t）的截短长度为5Tb，BTb=0.3，Ф（t）的抽样速率fs=8fb（fb=1/Tb=2.4 kbit/s ），量化电平Q=10bit/抽样。图5为FPGA平台上实现的顶层RTL（寄存器传输级逻辑）原理图。

该 GMSK数字调制器的最高时钟频率达到202.8 MHz，对FPGA资源占用分别为：4输入查找表（即 LUT）71个，Slices 293 个，BlockRAMs 1个。

3 仿真及结果分析

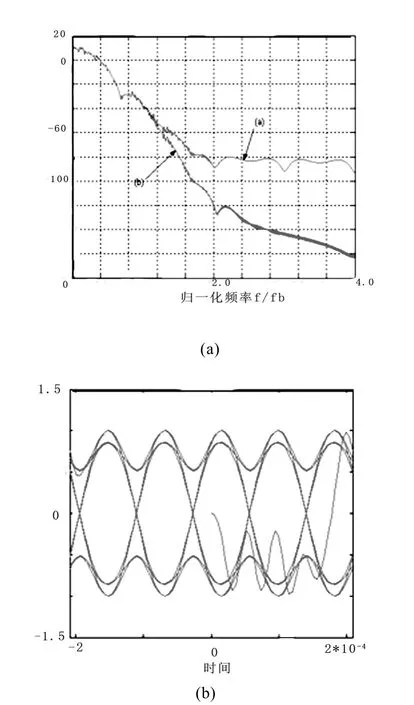
图6 GMSK基带已调信号功率谱密度及仿真眼图，

因为 GMSK信号的功率谱密度可看为将基带波形I（t）或Q（t）的功率谱搬移到载频上，所以求GMSK信号功率谱只需计算基带信号功率谱即可。用MATLAB对FPGA时序仿真后所得的数据进行处理，这里采用Welch法对GMSK基带信号进行功率谱估计[8]。如图6所示，曲线（a）表示图4中正弦余弦查找表输出端的谱估计图。可以看出，曲线（a）存在着由于抽样造成的副瓣，影响了功率谱性能。因此必须加低通滤波器来抑止高频分量。选用3 dB带宽为2.88 kHz的32阶数字低通滤波器，使得基带已调信号经低通滤波后的功率谱如图6的曲线（b）所示。由仿真得到的功率谱和眼图可以证明，这种GMSK数字调制器产生的基带已调信号具有良好的功率谱特性，能够满足电力线通信数据传输的要求。

[1] Rastislav Roka, Modelling of transmission channels over the low-voltage power distribution network.Journal of electrical enginnering, Vol.56, No.9-10,2005, 1-9.

[2] 耿煊等, 低压电力线通信的信道特性分析及模型研究, 电力系统通信. 2004, 4: 43-54.

[3] 陈萍等编著. 现代通信实验系统的计算机仿真. 国防工业出版社, 2003. 4: 243-254.

[4] 郭梯云等. 数字移动通信. 人民邮电出版社. 1996.

[5] M.Mouly and M.B. Pautet. The GSM system for mobile communications. Palaiseau, 1992.

[6] 罗来源, 肖先赐. 基于线性近似的GMSK信号调制.信号处理, 2002, 18（4）: 363-364.

[7] 张德纯,王兴亮 主编. 现代通信理论与技术导论.西安: 西安电子科技大学出版社, 2004, 10: 109-114.

[8] 庞沁华, 李卫东, 黄宇红. 数字移动通信高斯最小移频键控调制器. 北京邮电大学学报, 1994, 17（4）:20-25.

[9] 朱卫华, 黄乡佩, 卢桂荣. 基于FPGA的高精度数字移相低频正弦波发生器设计[J]. 微计算机信息 ,2005, （07）.