混合Cayley图的谱*

陈淑苹 陈金阳 谢 涛

(湖北师范学院数学与统计学院，湖北黄石435002)

0 引言

近30年，人们开始研究图的代数性质，随着计算机科学的迅猛发展，这个领域中的大量研究已经逐渐由国外向国内渗透.图论的代数性质也能被运用于许多领域，如通信理论、微软工程等.

为了把图和代数结合起来，学者们需要先引进一个概念，即图的邻接矩阵:v × v 矩阵A(G)=［aij］，其中aij是连接vi和vj的边的数目.这样每个图都能有相应的邻接矩阵和它对应，那么我们在研究图的代数性质时，实际上就是研究这个图相对应的邻接矩阵.邻接矩阵的一个重要的不变量就是它的特征值，所以研究图的特征值是非常重要的.图的M－特征值是图矩阵M 的特征值.图的M－谱是由M－特征值序列组成记做Spec M(G).如果Spec M(G)= Spec M(H)，则称G 和H 是M－同谱图，并表示为G－M H.记G 的M－同谱类为［G］M ={H|H－MG}.若对于任意满足G－M H 的图H 都有，则称G 是由M－谱所确定的.

Cayley 图是A.Cayley 在1878年提出的，当时是为了解释生成元和群定义的关系而提出的，但是由于它构造的简单性，品种的多样性和高度的对称性，越来越多的受到了图论学者的重视，成为群和图开辟出来的一个新领域.近几十年来，随着计算机的迅猛发展，人们发现Cayley 图是构造和设计互联网络的一种很好的数学模型，所以又获得了实际的应用，它的重要性就显得更加突出.

定义1［1］设G 是单位元为1G的群，S 是G 的任一不含单位元的非空子集，且满足S－1=S，则Cayley 图C(G，S)的顶点集合V = G，边集E ={(x，y)|x－1y∈S}.

Cayley 图是一类典型的点传递图.根据Cayley 图的定义，徐明曜给出了一类二部Cayley 图的概念:

定义2［1］设G 是单位元为1G的群，S 是G 的任一非空子集，则二部Cayley 图BC(G，S)的顶点集为V = G × {0，1}，边集E ={{(g，0)，(sg，1)}|g∈G，s∈S}.

而作为Cayley 图和二部Cayley 图的推广，陈金阳给出了混合Cayley 图的概念:

定义3［2］设G 是单位元为1G的群，S0，S1，S2是G 的子集，且满足Si=S－1i，1G∉Si，i=(0，1)，则混合Cayley 图MC(G，S0，S1，S2)的顶点集为V =G ×{0，1}，边集E =E0∪E1∪E2，其中当S2=ø 时，MC(G，S0，S1，S2)≅C(G，S0)∪C(G，S1);当S0= S1= ø 时，MC(G，S0，S1，S2)≅BC).

因此，Cayley 图和二部Cayley 图是混合Cayley 图的特殊情况.混合Cayley 图是陈金阳提出的一个全新的概念，它是一类半正则半传递图，因此是一类更具有一般性、拓扑结构更好的图类。除了陈金阳对其边连通性和超边连通性做了一些研究外，目前国内外同行还没有对此类图做过研究，因此具有较高的研究价值.

在本文中，我们根据混合Cayley 图和Cayley 图与二部Cayley 图之间的联系，研究了Cayley 图和二部Cayley 图的邻接矩阵在正规的情况下，混合Cayley 图的相邻矩阵，并计算出了混合Cayley 图的谱.

1 混合Cayley 图的谱

一个矩阵A∈Cn×n是正规的，如果A*A =AA*，这里的A*表示A 的复共轭转置矩阵.

引理1［3］Cayley 图的邻接矩阵是正规的.

引理2［3］二部Cayley 图的邻接矩阵是正规的.

引理3［3］假设A，B，C，D 是n × n 矩阵，|A|≠0，AC =CA，则.

引理4［3］设A 是一个正规矩阵，λ1，λ2，…，λn是它的特征值，则存在一个酉矩阵U 使得.

引理5［3］设λ1，λ2，…，λn是Cayley 图C(G，S)的特征值，则二部Cayley 图BC(G，S)的特征值是±λ1，±λ2，…，±λn.

引理6［4］设A，B 是可对角化的，若它们是可交换的，则A，B 是相似对角化的.

2 主要结果

定理1设λ1，λ2，…，λn是Cayley 图C(G，S0)的特征值，设κ1，κ2，…，κn是二部Cayley 图BC(G，S1)的特征值，如果C(G，S0)和C(G，S1)的邻接矩阵是正规的和可交换的，则混合Cayley 图MC(G，S0，S1，S2)的相邻矩阵的特征值是κ1±λ1，κ2±λ2，…，κn±λn.

证明设A，B，C 分别是BC(G，S1)，C(G，S0)和MC(G，S0，S1，S2)的邻接矩阵，则有，由引理3 得到:

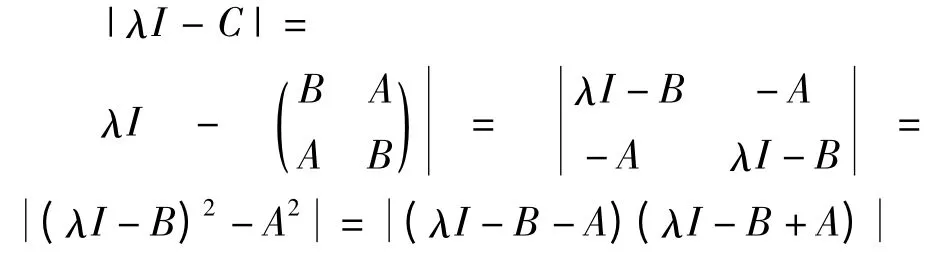
因为A 和B 都是正规的，由引理4 可知，存在一个酉矩阵满足:

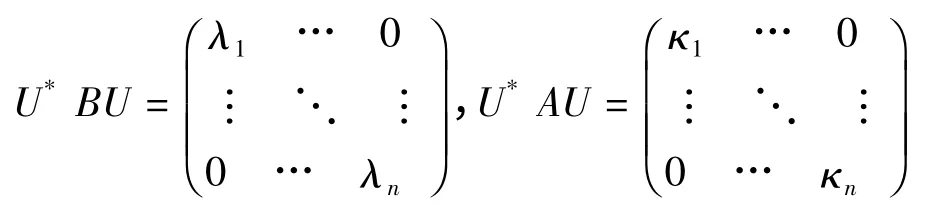
又因为A 和B 都是可交换的，由引理6 可得到:

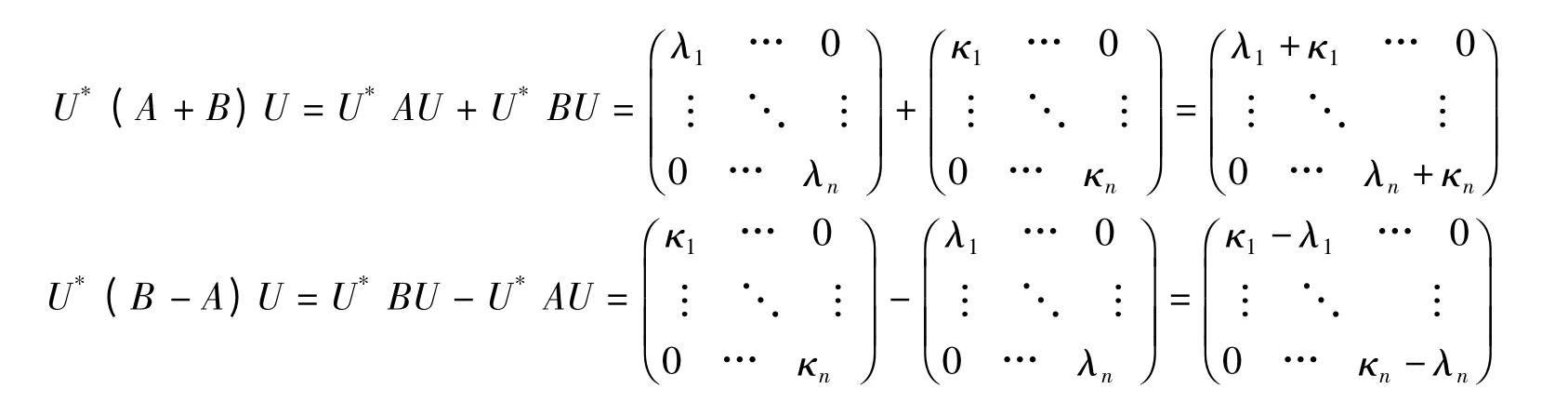
因此混合Cayley 图的MC(G，S0，S1，S2)的谱是κ1±λ1，κ2±λ2，…，κn±λn.

3 结束语

本文研究了混合Cayley 图的代数性质，把混合Cayley 图与代数问题结合起来，能有效的解决混合Cayley 图的许多问题.本文主要得到了混合Cayley 图连通时的谱，用更具体的数字化形式来衡量图的一些问题，为我们更加直观的研究图的性质带来了方便.

［1］徐明曜.有限群导引［M］.北京:科学出版社，2001:349－367

［2］Chen Jinyang，Meng Jixiang，Huang Lihong.Super edge－connectivity of mixed Cayley graph［J］.Discrete Mathematics，2009，309:264－270

［3］邹华.Bi－Cayley 图的一些代数性质［J］.新疆大学学报，2007(5):117－122

［4］R A Horn，C R Johnson.矩陈分析［M］.杨奇，译.北京:机械工业出版社，2005:156－174