基于粒子滤波框架联合仿射和外貌模型的目标跟踪

向志炎,曹铁勇, 潘竟峰

(1.解放军理工大学 通信工程学院,南京210007;2.解放军理工大学 指挥自动化学院, 南京210007)

1 引 言

近几十年来,目标跟踪引起越来越广泛的关注,已成为视觉领域的一个研究热点[1]。在许多诸如视频监控、交互式会议、人机交互、机器定位等视觉应用领域中,目标的跟踪问题都是亟待解决的主要任务之一,具有重要的研究价值和应用前景。

跟踪主要是监测视频序列中目标的位置变化,通常包括目标的旋转及其平移[2]。一般是在矢量空间,通过局部坐标点的确定与匹配,得到目标的旋转和平移等仿射参数,进而对目标实施跟踪。然而,常规的仿射变换并不是一个矢量空间,而是一个处理李群(仿射群)结构的曲线空间[3]。选择一组局域坐标点并且利用矢量空间的方法,是很难得到理想的结果(依赖于坐标点的选择)。基于这些考虑,文献[4]利用目标的几何结构定义了一个基于仿射群的状态方程,得到的跟踪结果更加健壮,鲁棒性更好。

在Isard 和Blake[5]的开创性研究之后,粒子滤波应用于大量的视觉跟踪问题[6-8]之中。这是由于在现实世界里,目标物体和其所在的环境都是随时间的变化而变化的,而使用蒙特卡罗的方法[9]能够处理这种非线性、非高斯以及非静态的滤波问题。研究表明,这种基于粒子滤波的方法是非常成功的。近年来,基于粒子滤波框架的目标跟踪方法层出不穷,根据其利用目标的特性不同,这些方法主要分为两大类:一类是利用目标的特征点[2,10],另一类是利用目标的外貌模型[11]。基于特征点的方法主要依赖于不同图像间的相关特征点,进行跟踪参数的估计,这种方法能对特征比较明显的目标进行比较好的跟踪,一般是处理环境比较简单的跟踪问题;基于外貌模型的方法虽然能很好地适应环境的变化,但是却忽视了目标本身的许多特性(如角点、轮廓等)。

针对彩色视频序列的目标跟踪问题,虽然彩色直方图对于跟踪非刚体目标有诸多优势[12],如尺度和旋转的不变性、对部分遮挡的健壮性以及计算的有效性等,但是这些还不足以处理更为复杂的问题,如大范围的遮挡、外貌的剧烈变化、复杂环境等。

基于以上考虑,为了对目标实施有效的跟踪,提出了基于粒子滤波框架的联合仿射和外貌模型的目标跟踪算法。该算法首先通过目标的特征点进行仿射参数的求解,对目标的姿势进行估计;然后将其嵌入到基于仿射群的粒子滤波框架之中,联合仿射模型和外貌模型进行似然估计,确定目标的最佳运动状态。

2 基于Sylvester 方程的仿射参数的求解

为了对目标的姿势进行估计,首先从一个已知目标姿势开始,并用一个矩形框进行标注。然后,利用文献[13]中SIFT(尺度不变特征转换)算法提取前后帧的相关特征点,也即匹配特征点,对于提取的特征点,由于可能存在误匹配,通过RANSAC 方法[14]来消除误匹配点。由于SIFT 算法提取的是整个图像的特征点,但是对于姿势估计,只需要保留矩形区域内的特征点,用于基于Sylvester 方程的仿射参数的求解[2]。

姿势估计的问题关键在于从前后两帧图像之间的匹配点求解出旋转和平移参数。首先将三维目标投影成二维目标,得到二维投影模型;然后假设(uit,vit)和(uit+1,vit+1)是第t 帧和第t+1 帧图像中相对应的投影点,则它们运动前后的位置有如下映射关系(即仿射变换):

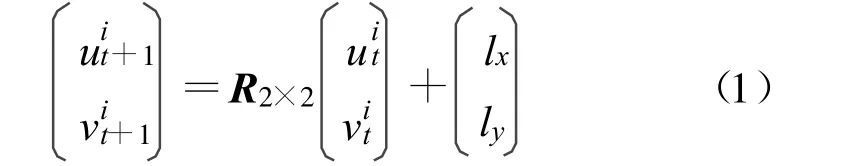
式中,i(i =1,2, …,M)表示第i 个匹配特征点, M为矩形框内特征点的总数;(lx,ly)表示的是平移矢量;R2×2是一个2×2 的旋转矩阵。

式(1)只是利用了一对特征点来估计旋转和平移参数的,而考虑到矩形框内所有的SIFT 匹配特征点,可以利用最小二乘估计的方法计算仿射参数,仿射参数的估计就变成了一个约束最优化问题,利用拉格朗日乘数法对其进行求解。最终得到一个矩阵方程:

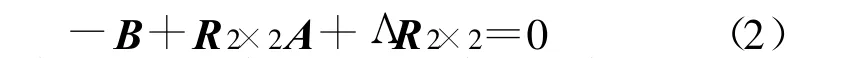
一旦通过解Sylvester 方程确定了前后两帧图像间的旋转参数,就可以通过下式计算平移矢量:

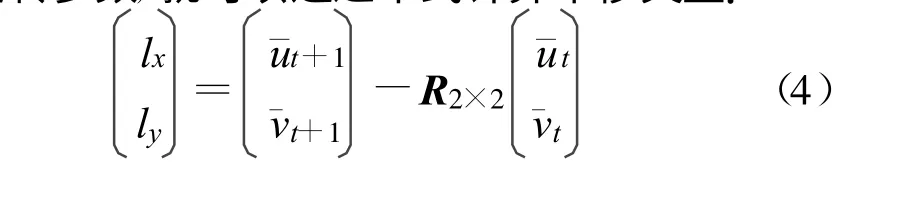
3 基于仿射群的目标跟踪

利用SIFT 特征点,通过Sylvester 方程计算仿射参数,估计出前后两帧图像之间的目标姿势的变化。而当前目标的状态是对过去所有状态积累更新得到的,这就可能会在状态更新的过程中产生误差累积的问题。因此,通过采用粒子滤波对仿射参数进行平滑估计,以避免误差及其产生的一些大的偏移。

3.1 基于仿射群的粒子滤波

在粒子滤波框架里,跟踪问题是利用概率密度函数对视频图像中的目标进行特征化。其概率密度函数是通过贝叶斯准则进行传递的:

式中,Xt表示在时刻t 被跟踪目标的状态变量,O1:t= o1,o2, …,ot表示的是一组观测值。跟踪过程是由观测模型p(otXt)和相邻时刻两状态之间的动态模型p(XtXt-1)来模拟。在这里,X 是一个二维仿射变换矩阵:

式中, R 是一个非奇异的2×2 的矩阵,L ∈R2。所有的仿射变换构成仿射群,即李群Lie group(G)。

仿射群G 是具有群结构的可微流形[4],具有群的乘积和逆运算,并且该群的单位元素Ι的切空间形成一个李代数Lie algebra(g),具有如下矩阵结构:

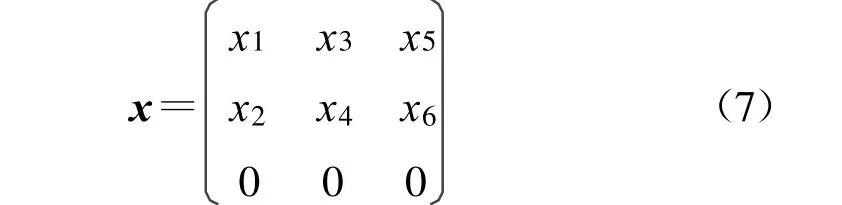
式中,xi∈R,且李代数等价于六维矢量空间。

仿射群之间的距离可以通过测地线(测地线是两点之间的最小长度曲线)的长度来测量。对于单位元素点I,给定任一矢量x ∈g,唯一的测地线将被确定。李群G 及其李代数g 之间是通过指数映射相对应的,exp:g ※G。其逆映射为, lg:G ※g。假定x ∈g 和X ∈G,相应的计算公式为

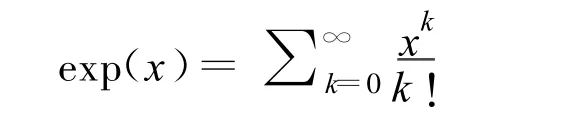
和那么,两个群元素X1,X2∈G 之间的测地线距离可被定义为

为了计算基于仿射群的采样均值 Xt,假设给定一组随机采样点Xjt-1(j=1,2, …,N),通过似然估计得到与权值wjt相对应的Xjt,并在每个时间步骤t时刻对采样粒子Xjt 进行重采样。对于旋转参数R1t,R2t, …,RNt,由于重采样的粒子都比较相似,因此,基于仿射群的旋转参数的采样均值可以近似地计算得到:

式中,Rt,max是对应于粒子重采样之前的最大权值的旋转矩阵,N 为采样粒子数。而平移矢量的采样均值 L t 可以简单地通过Ljt的算术平均得到。因此,采样粒子的平均状态为

3.2 基于仿射群的动态方程

假定状态传递方程模型是基于仿射群的一阶自回归(AR)过程[3],则状态的动态方程可表示为

式中,a 是AR 过程的参数;dWt =∑6i=0 wt,iEi是基于李代数g 的高斯噪声, wt是从高斯分布Np(0,∑p)中采样得到,并且wt= wt,1,wt,2, …,wt,6,∑p=diag(σ2s, σ2α, σ2θ, σ2,σ2x,σ2y)。Ei为李代数g 的基本元素:与每个Εi相对应的几何变换模式分别是尺度、面比、旋转、倾斜角、x 方向和y 方向的平移。

因此,状态的测量方程可表示为

式中, ∑q是一个六维的零均值的高斯白噪声的对角协方差矩阵。

3.3 观测似然函数

观测似然概率p(ot Xjt)描述的是一个粒子接近其真实状态的程度。通过使用彩色特性,基于概率主成分分析的外貌模型和特征模型这3 个单元进行似然估计。记分别是基于彩色、外貌模型和仿射模型(特征点模型)的第j 个采样的概率。为了简便,假设这3 个观测似然概率值是相互独立的,那么,可以通过将这3 个观测似然概率的相乘得到总体似然函数:

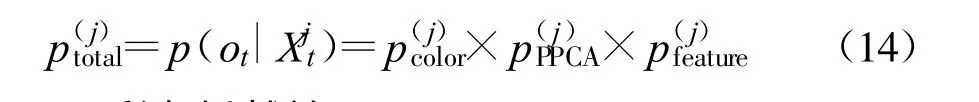
3.3.1 彩色似然单元

彩色分布对非刚体、旋转以及部分遮挡具有鲁棒性,因而可以被用作目标模型进行似然估计[12]。假设彩色分布被离散地分成m bin。然后,用函数H(lj)生成彩色直方图(H(lj)函数是将在位置lj的色彩分配到相应的bin 中)。本文的彩色直方图是基于HSV颜色空间使 用6 ×6 ×6 bin 生成 的。记 pt ={pjt}j=1,2,…,N为在时间步骤t 时刻的归一化的模型直方图和qt={qjt}j=1,2,…,N为在时间步骤t 时刻的归一化的粒子直方图。直方图分布p 和q 之间的一种比较流行的测量方法就是采用Bhattacharyya 系数:

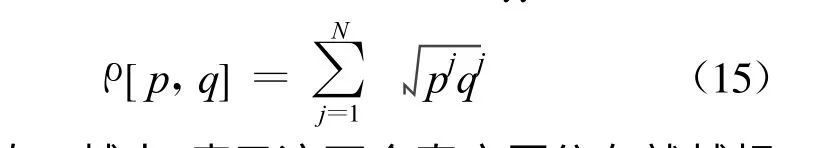
测量值ρ越大,表示这两个直方图分布就越相似。如果这两个归一化的直方图相同,那么它们之间的ρ值就等于1,并且表明它们完全匹配。因而,两分布之间的相似度就可以定义一个距离来进行测量:

因此,距离越小,表示分布越相似,对应地有更大的似然概率:

式中,p(j)color是方差为σ2c的高斯函数。

3.3.2 基于PPCA的外貌模型似然单元

目标的外貌由于许多外在的因素(如光照变化、照相机移动、照相机视角不同以及遮挡)和内在的因素(如姿势变化和形状畸变)都可能会发生剧烈的变化。因此,为了应对这些变化并实现有效跟踪,使用基于概率主成分分析的外貌模型进行目标跟踪[11]。给定一个新的由状态Xt预测的观测值ot,那么这个ot可以看成是从目标外貌模型特征向量Us张成的一个子空间所得,且该子空间的中心即为均值μs,因而,外貌子空间与观测值之间的距离可以定义为

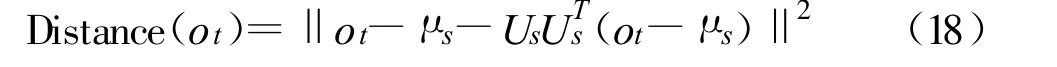
因此,由外貌子空间产生的采样点j 的似然概率为

同时,为了降低噪声的影响,在计算p(j)PPCA时,采样归一化的误差范数代替欧式范数‖x‖2去除异常值。

3.3.3 仿射模型似然单元

通过基于仿射群的自回归过程对目标的状态进行预测,仿射参数也会随着状态的变化而变化。设R(j)2×2E(j=1,2, …)为第j 个粒子变换矩阵,l(j)E是根据式(4)计算得到的平移参数。为了计算仿射特征点模型的似然概率p(j)feature,首先将第t 帧图像的特征点投影到第t +1 帧图像上, 然后计算投影点

式中,i 表示的是特征点的指针。由于SIFT 算法提取的特征点通常很多,这就很难保证所有相关的特征点之间相匹配,也即是,对于每一个i,都有u(j)it+1E=u(j)it+1和v(j)it+1E=v(j)it+1。所以,可以清晰地观察到,在第t+1 帧图像里,投影点与相应的匹配点之间的距离越小,相应的权值越大,就越接近真实状态。因此,仿射模型的似然概率为

4 实验结果

为了评估所提出的算法的有效性和鲁棒性,选取了几段视频分别进行验证。首先手动地初始化目标跟踪的矩形框。在仿真实验中,考虑到跟踪区域像素会随着矩形窗的变化而变化的问题,同时为了特征表示,每个目标区域都被重新调整为32×32 大小的图像块。对于基于概率主成分分析的外貌模型,选取的特征向量的个数为16,考虑到效率与效果的平衡,其遗忘因子设为0.95,用于特征向量更新的图像块大小设为5。每帧图像随机采样的粒子数设为400(除特别说明外),跟踪的目标用矩形框表示。

图1 是PetsD1TeC1 序列中白色汽车的跟踪结果,共选取了200 帧,其图像分辨率为384×288 像素,帧率为30 frame/s。这是固定摄像机拍摄的视频,从图中可以观察到,目标由远及近,尺度逐渐变大;在第133 帧,灯杆轻微地遮挡了目标;存在与目标外貌及其相似的背景(第8、72、98、133 帧)。从矩形跟踪框可以看到,虽然目标的外貌没有发生大的改变并且背景中存在大量与之类似的目标物体,但是所提出的算法能够利用目标的特征点变化这一特性,很好地处理了这些变化, 达到了预期的实验效果。

图1 PetsD1TeC1 序列的跟踪结果Fig.1 The tracking results of PetsD1TeC1 sequence

图2 是直升机序列的跟踪结果,选取了780 帧,其图像分辨率为320×240 像素,帧率为15 frame/s。图2 中,直升机模型以变化的速度随机移动,并且经历较大的尺度和姿势的变化、遮挡以及复杂背景,如跟踪目标的姿势和尺度的变化(第16、142、283、756帧),目标经历了严重遮挡(从第280 到283 帧, 其中,第281、282 帧目标几乎完全被人头遮住)和复杂背景(第280、283、498、552、593 帧,其中,在第552、593 帧图像中,由于目标与背景的颜色非常接近,导致跟踪的目标很难被发现),这些情况都使得我们的跟踪任务具有相当的挑战性。然而,从图2 的实验结果可以看出,本文的跟踪方法能很好地处理这些问题,取得了非常好的实验效果。这是因为在粒子滤波框架内基于彩色分布和PPCA 的思想,能很好地适应环境和外貌的变化,甚至能克服先前文献中提到的目标丢失和暂时偏移等问题。

图2 直升机序列的跟踪结果Fig.2 The tracking results of helicopter sequence

4.1 算法有效性验证

为了验证在粒子滤波框架内插入Sylvester 方程的有效性,如图3 所示,首先将直升机序列转化成灰度图像, 通过比较可以看出,插入Sylvester 方程的PPCA 的跟踪方法能有效地克服遮挡(如从第280 到283 帧),而仅仅基于文献[11]的PPCA 方法在经历严重遮挡之后,却丢失了目标。

图3 基于文献[11] 的跟踪结果(虚线框)和基于仿射及外貌模型的跟踪结果(实线框)Fig.3 The tracking results of the method based on Reference[11] (dashed)and our proposed approach(solid)

同时,为了验证本文嵌入Sylvester 方程到基于仿射群的粒子滤波框架的跟踪算法的有效性,与文献[3]中的基于仿射群的粒子滤波框架的跟踪算法进行比较。选取一段灰度视频David 序列,其图像分辨率为320×240 像素,帧率为15 frame/s。在这次实验中,我们选取的采样粒子数为200。图4 是两种跟踪方法比较的结果,从跟踪结果可以看出,当跟踪目标的姿势发生大的变化时,文献[3]的跟踪精度下降了(如第192、382、418 帧),以至于发生了较大的偏移;相比较而言,本文提出的方法提供了一个更为精确的跟踪结果, 这是由于通过SIFT 特征点,Sylvester 方程能更有效地对仿射参数进行估计,使得跟踪更加稳定、准确。

图4 基于文献[3] 的跟踪结果(虚线框)和基于仿射及外貌模型的跟踪结果(实线框)Fig.4 The tracking results of the method based on Reference[3] (dashed)and our proposed approach(solid)

4.2 算法鲁棒性验证

为了验证所提出的算法的健壮性, 也与文献[12]中基于彩色粒子滤波算法的目标跟踪结果作了比较。如图5 所示,第一行为文献[12] 中算法的跟踪结果,第二行为本文所提算法的目标跟踪。两者比较可以看出:基于彩色的粒子滤波有较大偏移(如第18 帧与第166 帧椭圆的位置变化),在复杂背景下丢失了所跟踪的目标(第552 帧),并且在实验中发现算法的适应性和稳定性都不是很好;而本文提出的算法克服了偏移并对目标物体成功地实施了跟踪,具有良好的鲁棒性。

图5 基于文献[ 12] 中的算法与本文提出的算法的跟踪比较Fig.5 Com parison between the tracker based on Reference[ 12] and the proposed tracker

5 结 论

本文提出的基于粒子滤波框架的联合仿射和外貌模型的目标跟踪算法,有效地解决了复杂情况下的目标跟踪问题。首先利用Sylvester 方程求解仿射参数,对目标的姿势进行估计,这样就可以在后面的粒子滤波过程中使得随机采样更趋于正确的状态。通过将仿射参数嵌入到粒子滤波框架,利用基于仿射群的粒子滤波对仿射运动参数进行平滑估计。充分利用外貌模型和仿射特征点模型的优势进行似然估计,得到了最佳的采样均值,提高了滤波的效果。通过实验分析,并与其他相关文献算法对比,本文算法的有效性和鲁棒性得到了很好的验证。而对于跟踪目标丢失或进出视频画面的情况,本文算法由于是手动标定目标,难于继续对目标实施跟踪,同时,为了适应实际应用的需要,在后续的研究工作中,打算引入对目标的自动检测,以提高目标跟踪算法的适应性和实用性。

[ 1] Yilmaz A, Javed O, Shah M.Object tracking:a survey[ J] .ACM Computing Surveys,2006,38(4):1-45.

[ 2] Chen Chong, Schonfeld D.A particle filtering framework for joint video tracking and pose estimation[ J] .IEEE Transactions on Image Processing, 2010,19(6):1625-1634.

[ 3] Kwon J, Park F C.Visual tracking via particle filtering on the affine group [ J] .The International Journal of Robotics Research, 2010, 29(2-3):198-217.

[ 4] Li Min, Chen Wei, Huang Kaiqi, et al.Visual tracking via incremental self-tuning particle filtering on the affine group[ C]//Proceedings of 2010 IEEE conference on Computer Vision and Pattern Recognition.San Francisco:IEEE, 2010:1315-1322.

[ 5] Isard M, Blake A.Condensation-conditional density propagation for visual tracking[ J] .International Journal of Computer Vision, 1998, 29(1):5-28.

[ 6] Ferrari V, Tuytelaars T, Van Gool L.Real-time Affine Region Tracking and Coplanar Grouping [ C]// Proceedings of 2001 IEEE Com puter Society Conference on Computer Vision and Pattern Recognition.Hawaii:IEEE, 2001:226-233.

[ 7] Pan Pan, Schonfeld D.Video Tracking Based on Sequential Particle Filtering on Graphs[J] .IEEE Transactions on Image Processing, 2011, 20(6):1641-1651.

[8] Djuric P M, Vemula M, BugalloM F.Target Tracking by Particle Filtering in Binary Sensor Networks[ J] .IEEE Transactions on Signal Processing,2008,56(6):2229-2238.

[9] Kitagawa G.Monte carlo filter and smoother for non-Gaussian nonlinear state space models[ J] .Journal of Computational and Graphical Statistics, 1996,5(1):1-25.

[10] Singh Manku G, Jain P, Aggarwal A, et al.Ob ject tracking using affine structure for point correspondences[C]// Proceedings of 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Puerto Rico:IEEE, 1997:704-709.

[11] Ross D, Lim J, Lin R S, et al.Incremental learning for robust visual tracking[ J] .International Journal of Computer Vision,2008,77(1):125-141.

[12] Nummiaro K, Meierb E K, Van Gool L.An adaptive color-based particle filter[ J] .Image and Vision Computing,2002,21(11):99-110.

[13] Lowe D G.Distinctive image features from scale-invariant keypoints[ J] .International Journal of Computer Vision,2004, 60(2):91-110.

[14] Fischler M A, Bolles R C.Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J] .Communications of the ACM, 1981,24(6):381-395.