非均匀内水压力作用下的坝下箱涵结构计算
蔡勇斌,刘月琴,蔡勇平,蔡晓鸿
(1.江西省吉安市水利局,江西吉安343000;2.江西省吉安市水利水电规划设计院,江西吉安343000)
0 引言
箱涵是坝下涵管常见结构型式之一,坝下箱涵受土压力作用的内力与变位计算已有成熟的结构力学解法[1],但坝下箱涵受非均匀内水压力作用,特别是侧墙受梯形荷载作用的内力与变位计算却鲜见介绍。本文依据弹性地基梁理论,将箱涵底板与顶板分别视为承受内水压力P1、P2作用的固端弹性地基梁,将箱涵侧墙视为底端承受内水压力P1、顶端承受内水压力P2梯形分布荷载作用的固端弹性地基梁,采用左手坐标系,按弹性地基梁初参数法与地下框架结构位移法弯矩与剪力正、负号匹配关系,建立了箱涵底板、顶板、侧墙载常数计算方法,给出了箱涵受非均匀内水压力作用时的内力与变位解析计算式。
1 坝下箱涵载常数
1.1 箱涵底板载常数
坝下箱涵底板可简化为受均布内水压力P1作用的两端固定弹性地基梁,采用左手直角坐标系,其计算简图见图1。
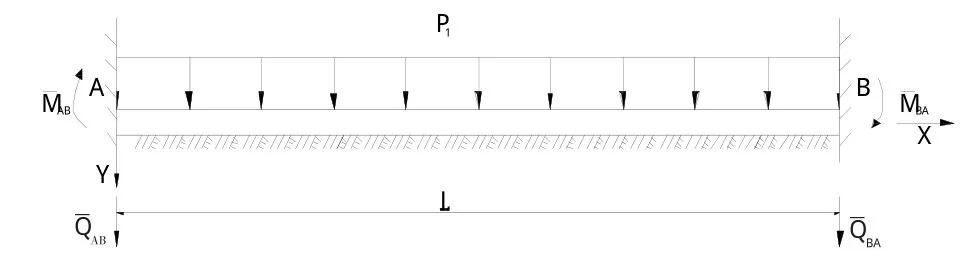
图1 坝下箱涵底板载常数计算简图Fig.1 Calculation diagram of load constants of the bottom plate
由弹性地基梁受均布荷载P1作用下的初参数变位解,且注意到箱涵底板左端A为初始截面,杆端弯矩MˉAB、MˉBA以顺时针方向为正,杆端剪力以指向地基方向(沿y轴方向)为正,于是箱涵底板挠度计算式为
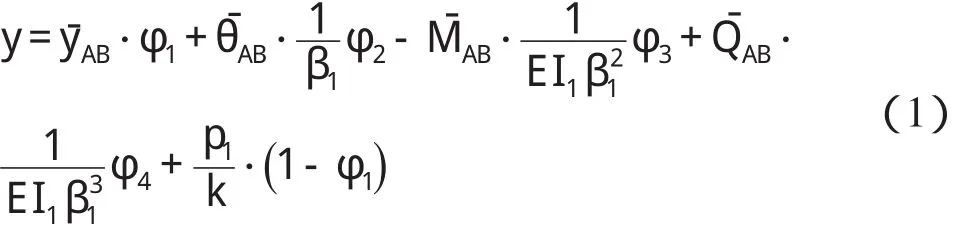
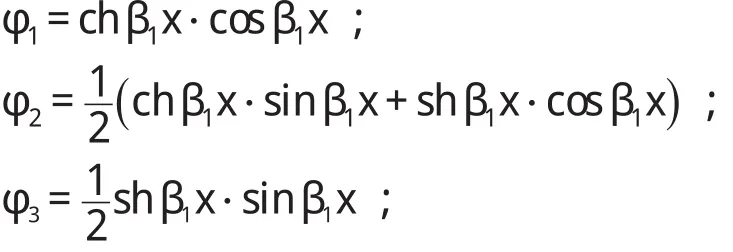
β1为坝下箱涵底板特征系数k为坝下箱涵弹性抗力系数,若不计地基弹性抗力,则在计算时k可取很小值;E为坝下箱涵混凝土弹性模量;I1为坝下箱涵底板截面惯性矩。
据箱涵底板载常数计算简图,由左端边界条件y|x=0==0,θ|x=0==0,据式(1)可得底板挠度方程、转角方程、弯矩方程及剪力方程。
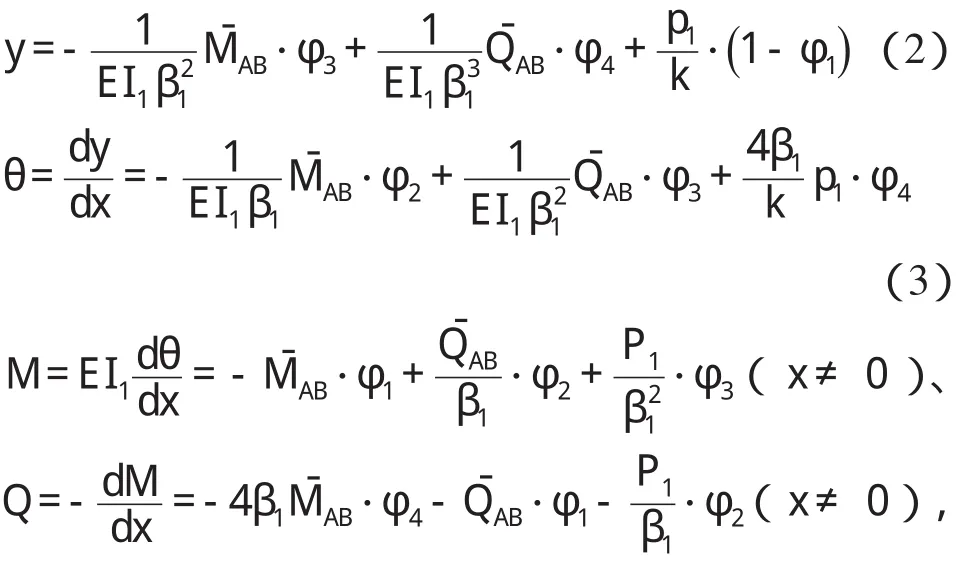
又利用底板右端边界条件y|x=l==0,θ|x=l==0,据式(2)、式(3)可得底板左端及右端载常数。
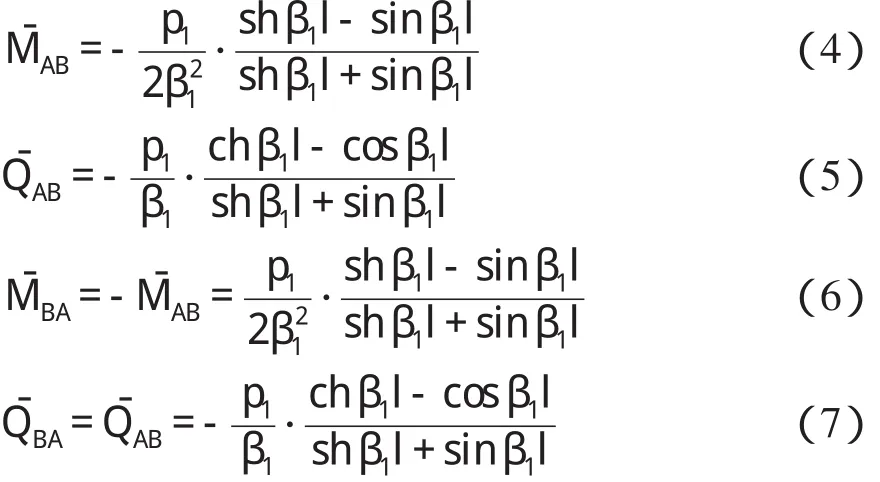
1.2 箱涵顶板载常数
坝下箱涵顶板可简化为受均布内水压力p2作用的两端固定弹性地基梁,计算简图如图2。
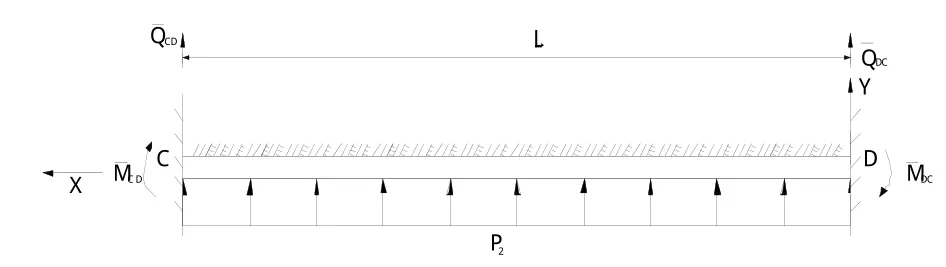
图2 坝下箱涵顶板载常数计算简图Fig.2 Calculation diagram of load constants of the roof
类似于坝下箱涵底板载常数的推导,且注意到箱涵顶板所受均布内水压力p2作用方向垂直向上,可得箱涵顶板左、右固端载常数分别为:
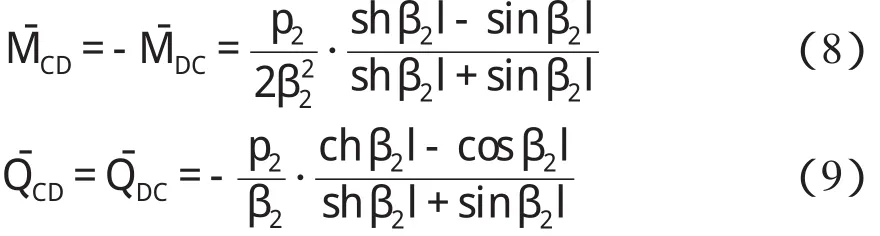
式中,为坝下箱涵顶板特征系数;I2为箱涵顶板截面惯性矩;其余符号意义同前。
1.3 箱涵左侧墙载常数
坝下箱涵左侧墙为受向左方向作用的内水压力梯形荷载两端固定弹性地基梁,其计算简图如图3所示。
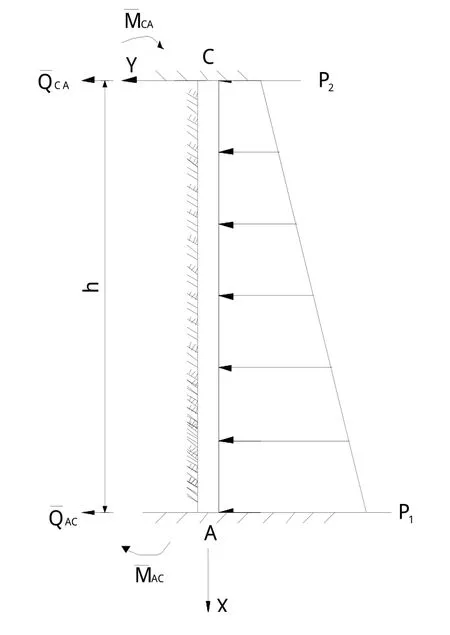
图3 坝下箱涵左侧墙计算简图Fig.3 Calculation diagram of the left side wall of the box cul⁃vert beneath dam
由弹性地基梁受梯形荷载作用下的初参数变位解,且注意到剪力以指向地基方向为正,于是有箱涵左侧墙挠度计算式
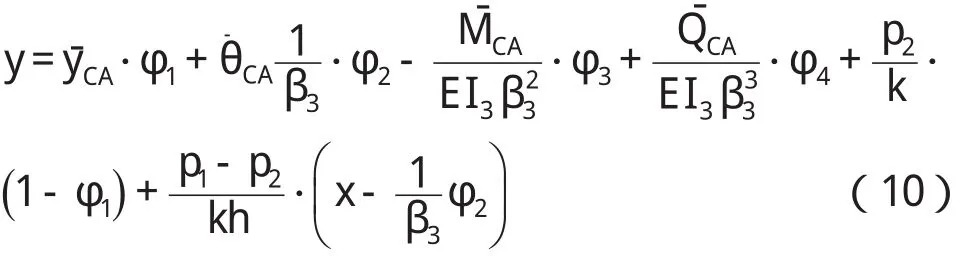
由箱涵侧墙顶端边界条件y|x=0==0;θ|x=0==0,可得箱涵侧墙挠变方程、转角方程、弯矩方程及剪力方程:
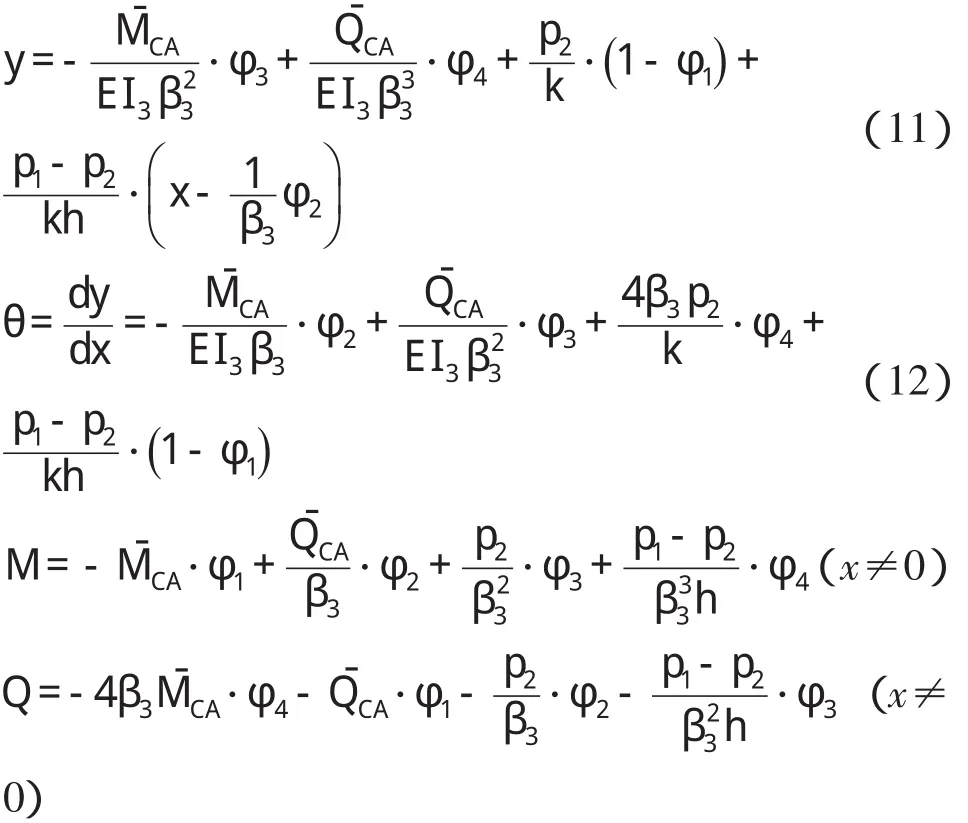
利用箱涵左侧墙底端边界条件y|x=h==0;θ|x=h==0,据式(11)、(12),可得箱涵左侧墙顶端及底端载常数:
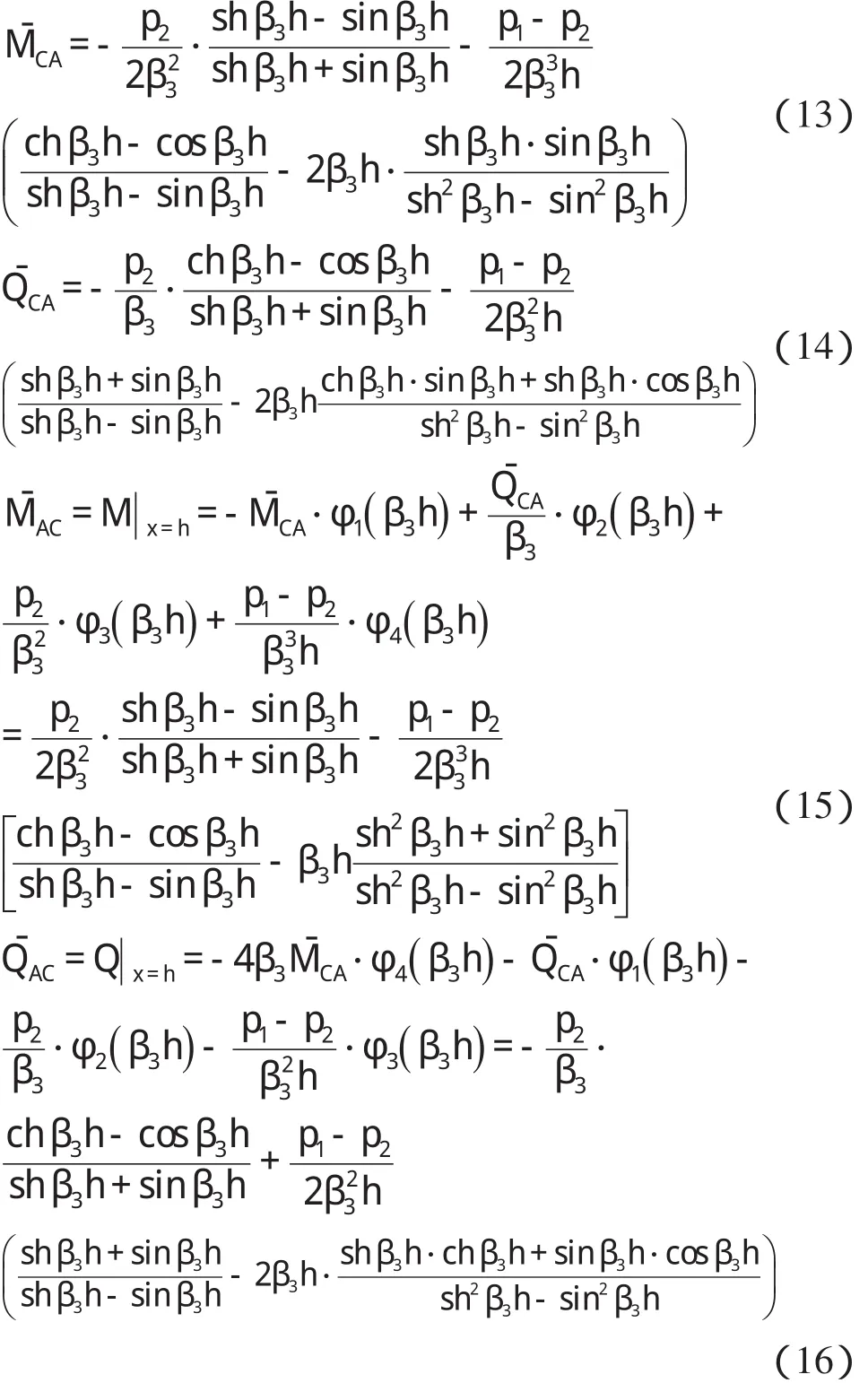
1.4 箱涵右侧墙载常数
坝下箱涵右侧墙为受向右方向作用的梯形内水压力荷载两端固定弹性地基梁,其计算简图如图4所示。
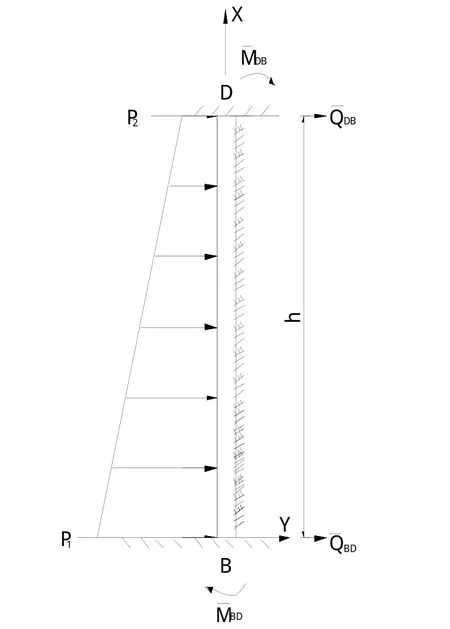
图4 坝下箱涵右侧墙计算简图Fig.4 Calculation diagram of the right side wall of the box cul⁃vert beneath dam
类似于坝下箱涵左侧墙载常数的推导,据对称性,可得箱涵右侧墙顶端及底端载常数为

2 坝下箱涵形常数
据如下弹性地基梁无载段挠度方程、转角方程、弯矩方程与剪力方程式
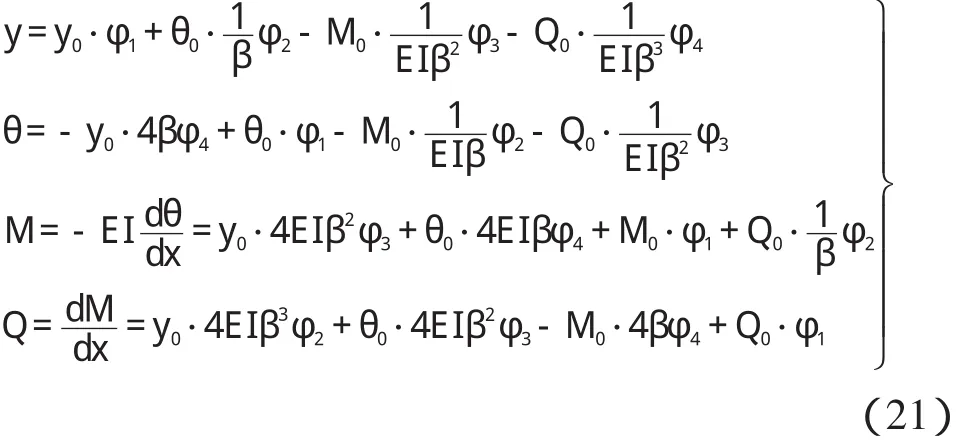
可推导出如下弹性地基梁两端转动形常数与移动形常数(图5)
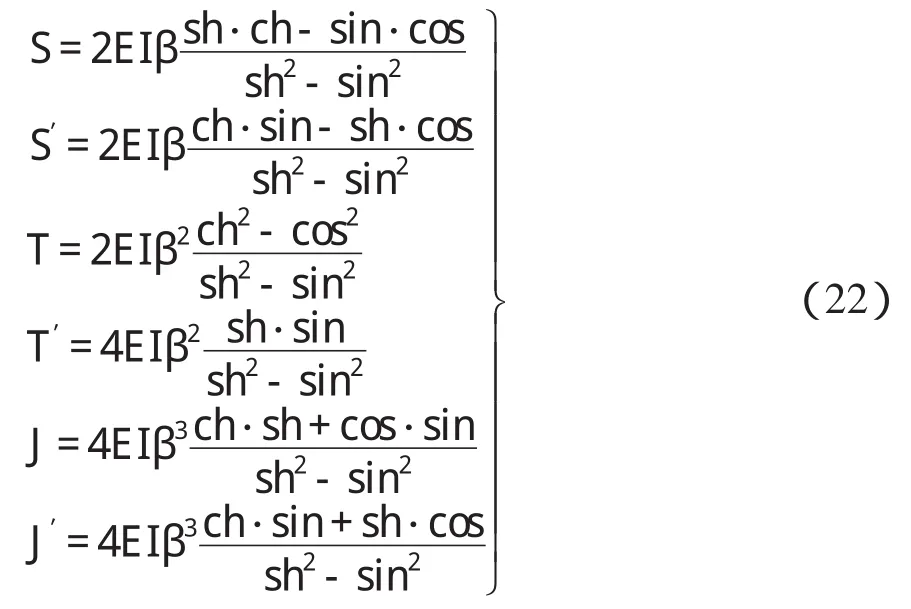
式中:sh、ch、sin、cos分别为sh βl、ch βl、sin βl、cosβl的简写。
S为梁端发生单位转角时的本端弯矩;S′为梁端发生单位转角时的远端弯矩;
J为梁端发生单位移动时的本端剪力;J′为梁端发生单位移动时的远端剪力;
T为梁端发生单位转角时的本端剪力,或梁端发生单位移动时的本端弯矩;
T′为梁端发生单位转角时的远端剪力,或梁端发生单位移动时的远端弯矩;
其它符合意义同前。
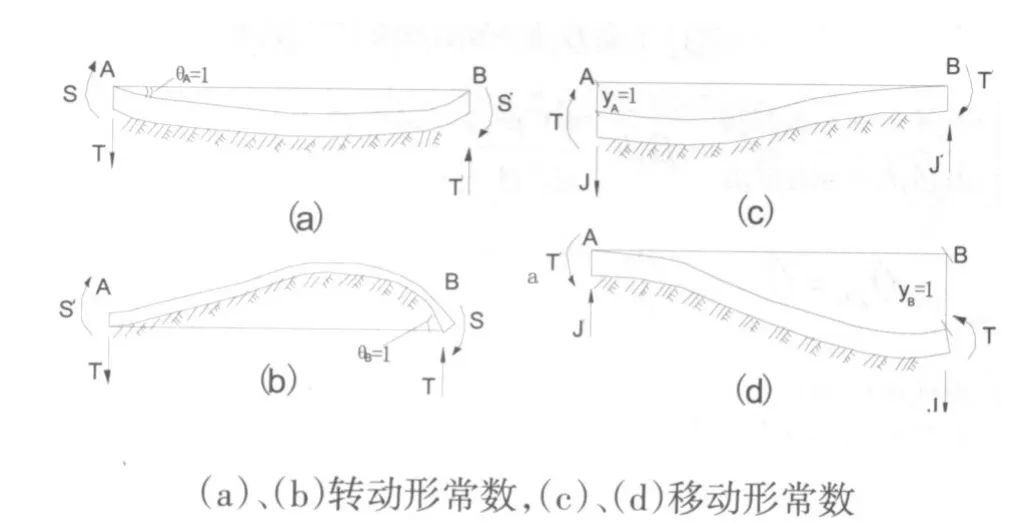
图5 弹性地基梁形常数计算简图Fig.5 Calculation diagram of shape constants of elastic foun⁃dation beam
3 坝下箱涵结点平衡方程组
坝下箱涵地基梁杆件在内水压力荷载p作用下,将产生固端弯矩和固端剪力,出现杆端位移(图6),于是据箱涵地基梁杆件载常数与形常数,采用叠加原理,可得箱涵杆件杆端内力计算式:
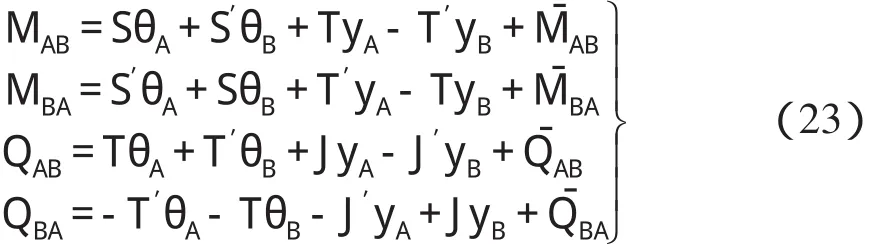
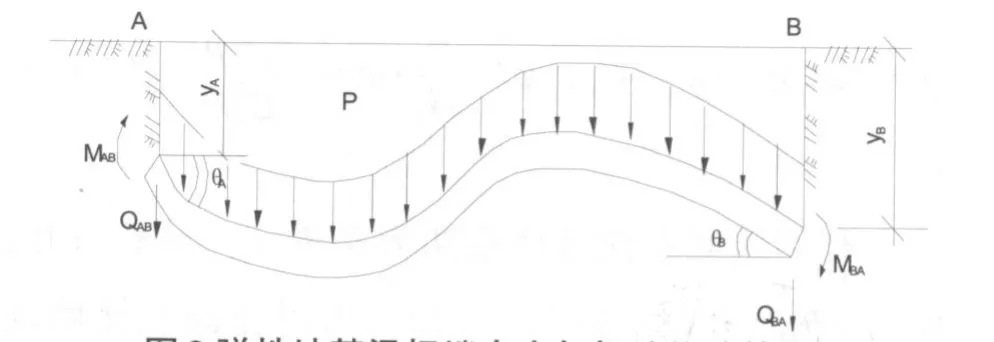
图6 弹性地基梁杆端内力与杆端位移简图Fig.6 Internal force and displacement at the end of the elastic foundation beam
式(23)也称为箱涵杆件转角位移方程。
式中:MAB、MBA、QAB、QBA表示箱涵杆件杆端内力;θA、θB、yA、yB表示箱涵杆件杆端位移;、、、表示箱涵杆件固端弯矩和固端剪力,即箱涵地基梁杆件载常数。
在得出箱涵杆件A B、A C;BA、BD;CA、CD;D C、D B的转角位移方程后,则可分别建立箱涵结点A、B、C、D的力矩平衡方程
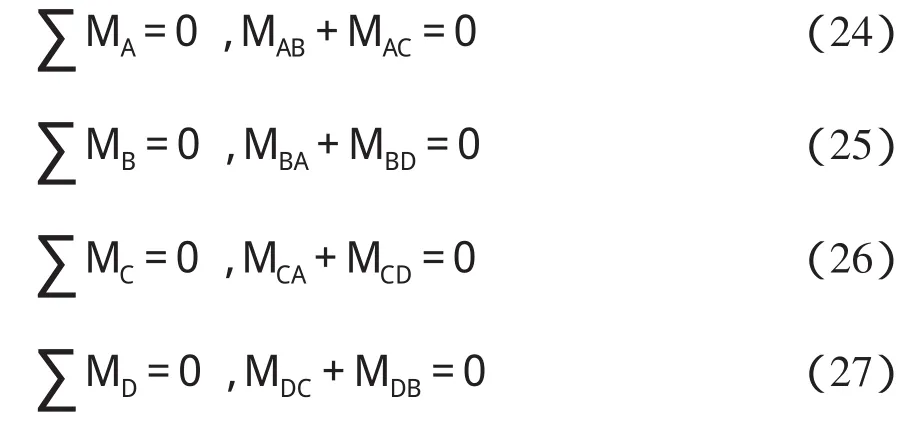
将箱涵杆件杆端内力计算成果代入式(24)~(27),联立求解便可得到箱涵结点转角与位移。
4 工程实例
某水库坝下箱涵采用竖井取水,箱涵坐落于土基上,为C20钢筋混凝土结构,混凝土弹性模量Ec=2.55×107kPa,土基弹性抗力系数k=10×103kN/m2。箱涵底板、顶板、侧墙厚均为d=0.3m,计算宽度l=1.5m,计算高度h=1.9m,净空尺寸1.2 m×1.6 m(宽×高)。底板承受内水压力p1=216 kN/m2,顶板承受内水压力p2=200 kN/m2。求箱涵在非均匀内水压力作用下的弯矩与剪力。
解:取单宽箱涵b=1.0 m进行计算与分析。
工程实际问题表明,箱涵结构与荷载轴对称,箱涵结点基本未知量只有θA与θC。下面计算箱涵特征参数。
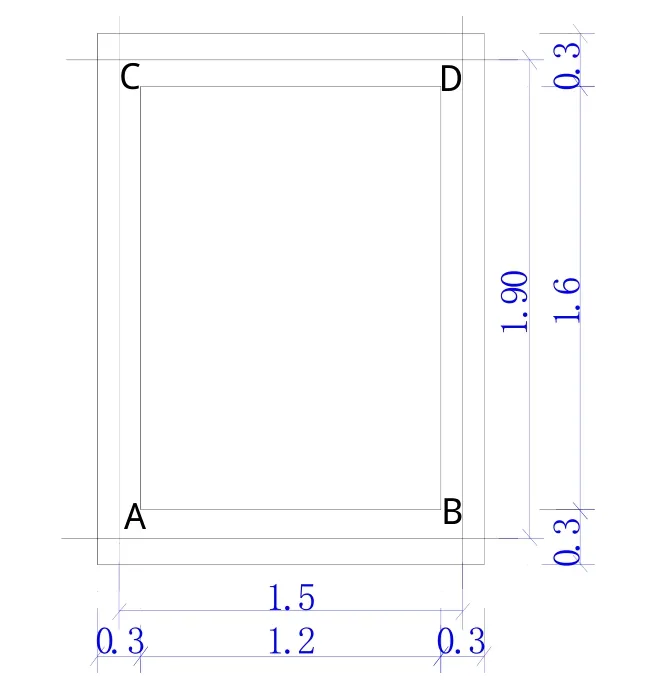
图7 坝下箱涵横剖面尺寸图Fig.7 Profile of the box culvert beneath dam
4.1 箱涵特征参数
(1)箱涵底板、顶板、侧墙的截面惯性矩I
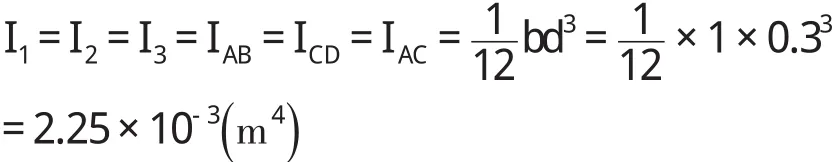
(2)箱涵底板、顶板、侧墙的特征参数β
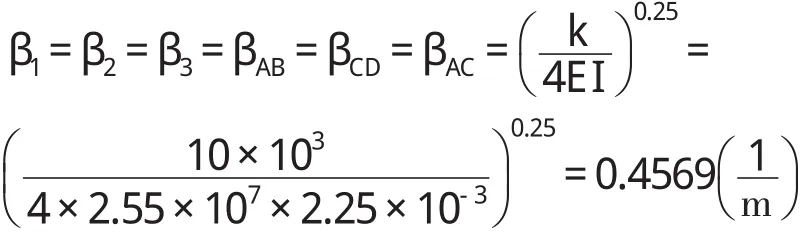
于是
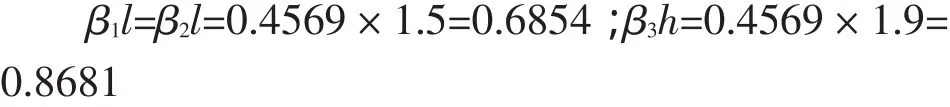
(3)箱涵底板、顶板、侧墙的形常数
箱涵底板受均布荷载作用,杆端对称转动,其形常数可将有关参数代入式(22)求算,即

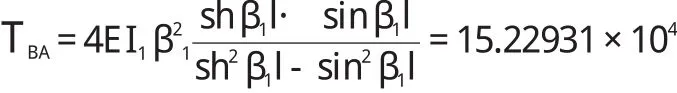
类似箱涵顶板的形常数为
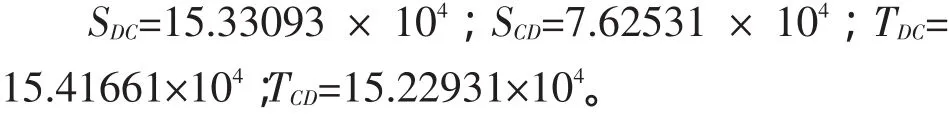
箱涵侧墙顶端、底端形常数分别为
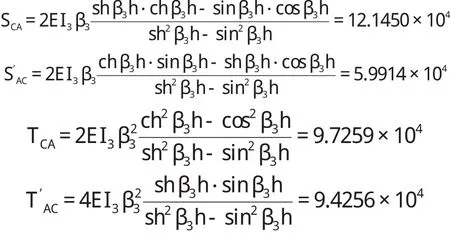
(4)箱涵底板、顶板、侧墙的载常数
箱涵底板的载常数可将有关参数值代入式(6)、式(7)求算,即
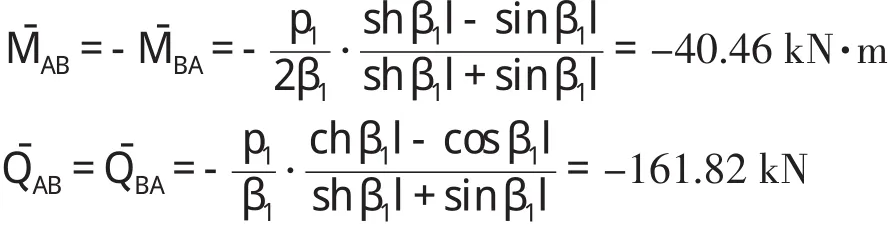
类似箱涵顶板的载常数可将有关参数值代入式(8)、式(9)求算,即有
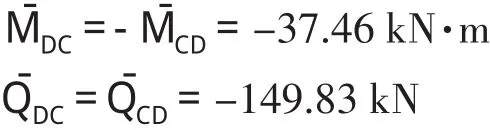
箱涵左侧墙顶端的载常数可将有关参数代入式(13)、式(14)求算,即有
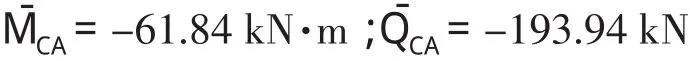
箱涵左侧墙底端的载常数可将有关参数值代入式(15)、式(16)求算,即有
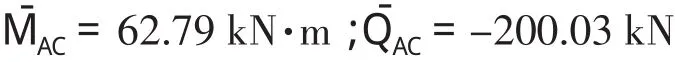
4.2 箱涵转角位移方程
鉴于箱涵结构力荷载关于竖向呈轴对称,于是箱涵刚结点转角存在关系θB=-θA,θc=-θD,且结点线位移为零。据式(23),可得箱涵结点A、C的变矩:
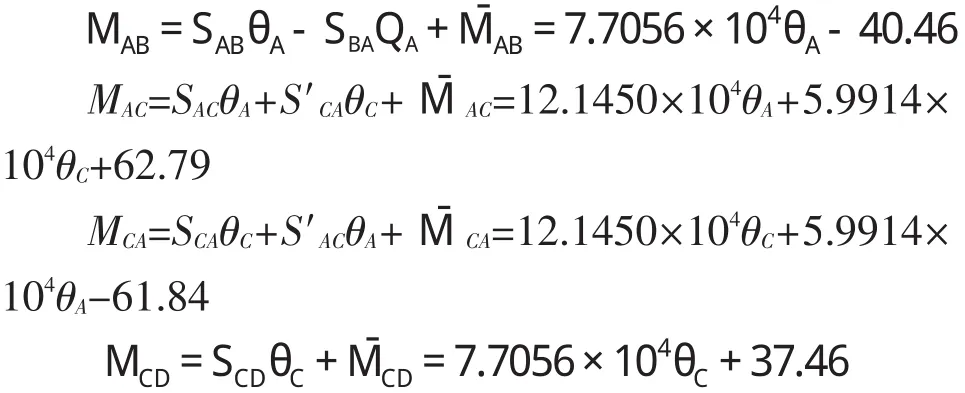
4.3 箱涵结点平衡方程
据式(24)及式(26),可列出箱涵结点A、C的力矩平衡方程
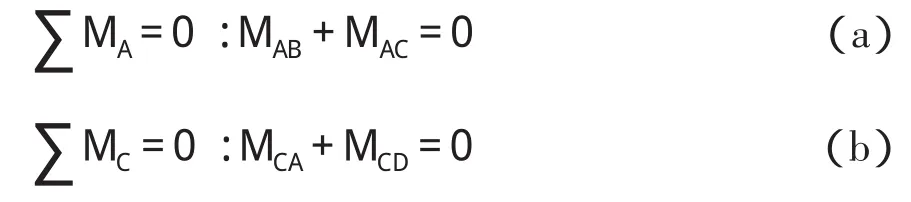
将箱涵转角位移方程中的MAB、MAC、MCA、MCD表达式代入式(a)、式(b)得
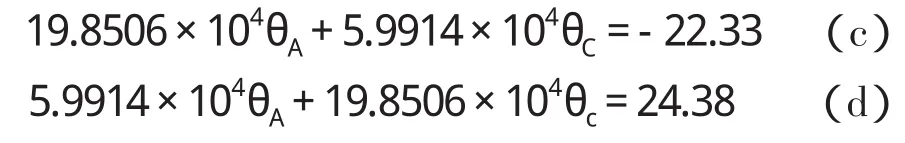
联立求解式(c)、式(d)得θA=-1.6455×10-4;θC=1.7248×10-4
4.4 箱涵杆端内力
将求得的θA、θC值代入箱涵底板、顶板、侧墙转角位移方程式(23)中第1式、第2式,得如下杆端弯矩
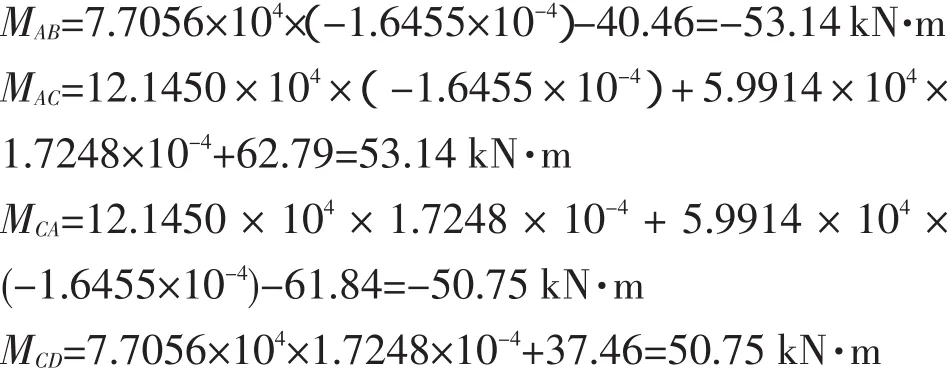
此外,据转角位移方程式(23)中第3式、第4式可求算出箱涵底板、顶板、侧墙杆端剪力
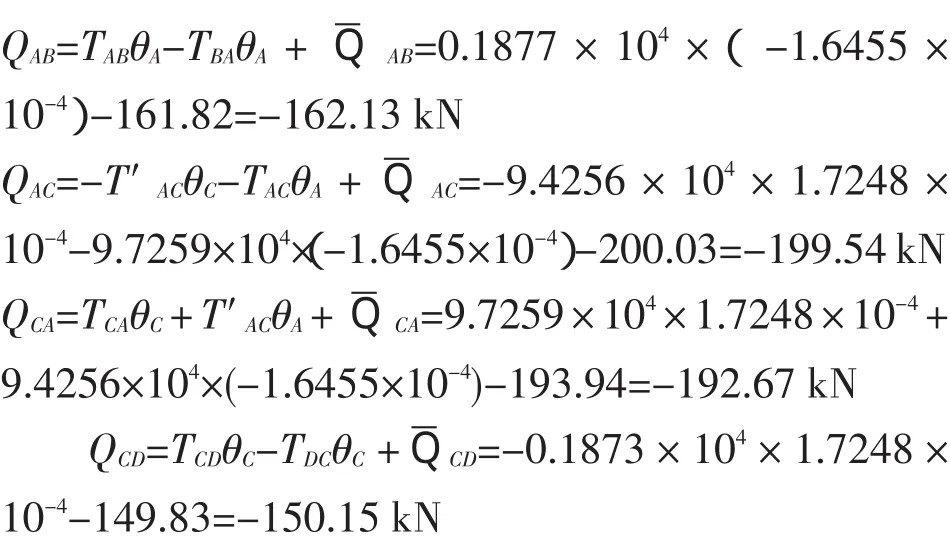
4.5 求底板、顶板的跨中弯矩与侧墙最大弯矩
据式(21),且注意到箱涵底板有y0==0,M0=MAB,Q0=-QAB,于是得
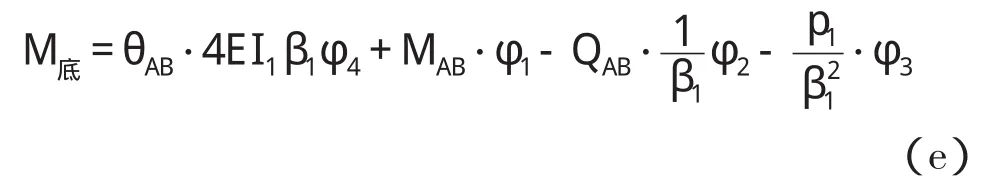
箱涵底板跨中处有:β1x=β1l=×0.4569×1.5=0.3427,查表得:φ1=0.9977,φ2=0.3425,φ3=0.0587,φ4=0.0068。并将以上计算值θAB、MAB、QAB及P1代入式(e),即得底板跨中弯矩为:
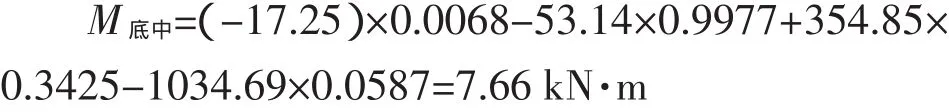
类似可得箱涵顶板弯矩计算式
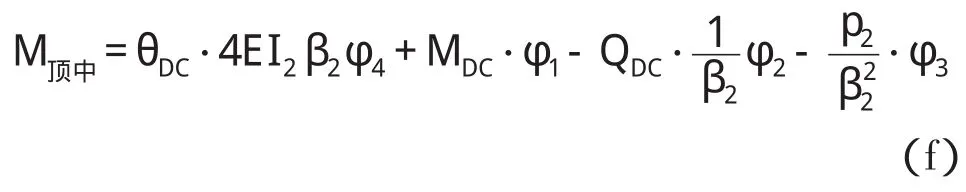
将有关计算值与查表值代入得

箱涵左侧墙受梯形荷载作用,类似于式(e),其弯矩计算式为
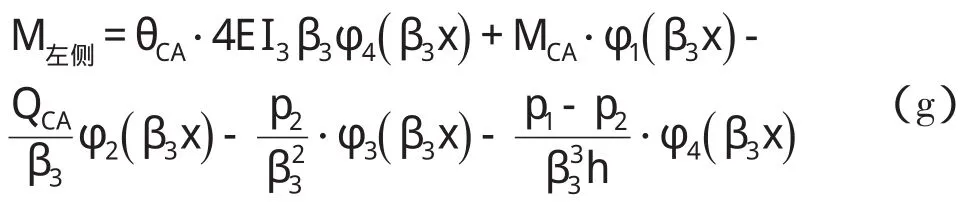
将有关参数值与计算值代入,得
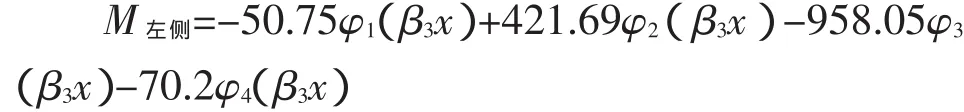
综合以上计算结果,可得如图8弯矩图。
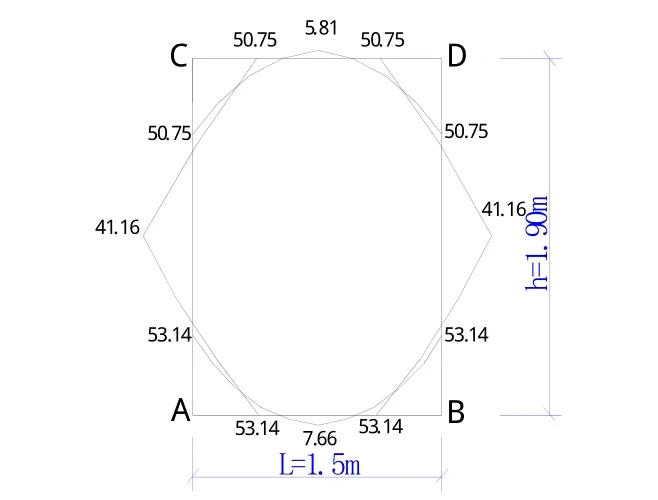
图8 坝下箱涵内水压力作用下弯矩图(单位:kN·m)Fig.8 Bending moment of the box culvert beneath dam under internal water pressure
5 结语
采用地下框架结构模型,按左手直角坐标系,采用初参数法分析弹性地基梁与位移法建立箱涵杆件转角位移方程,推导坝下箱涵受非均匀内水压力作用下的内力与变位计算式。工程实例计算成果表明,箱涵底板、顶板与侧墙相交直角处与杆件跨中部位通常为内力计算控制断面,弯矩取极值,特别是侧墙跨中部位外侧有可能与土压力荷载作用下的同向弯矩相叠加而加大结构内力。因此,为增强箱涵结点强度与刚度,消除或减小转角处的应力集中,采取设置贴角、配设构造钢筋及加强侧墙跨中部位配筋等工程结构措施是必要的。此外,尚需指出,计及地基弹性抗力,可降低箱涵杆件最大弯矩值,且所获成果可毫无困难地直接应用于水工矩形压力隧洞洞段、矩形竖井与矩形调压室衬砌结构计算。■
[1]熊启钧.涵洞[M].北京:中国水利水电出版社.2006.
[2]潘家铮.水工结构分析文集[M].北京:电力工业出版社.1981.
[3]龙驭球.弹性地基梁的计算[M].北京:高等教育出版社.1981.
[4]龙驭球,包世华.结构力学教程[M].北京:高等教育出版社.1988.
[5]蔡勇斌,周雪芳,蔡勇平,等.坝下涵管纵向内力计算与伸缩缝间距设计[J].大坝与安全,2012,(1).
[6]蔡勇斌,刘女英,蔡勇平,等.圆形坝下涵管结构内力与变位计算及抗裂验算解析法[J].大坝与安全,2010,(6).
[7]张志坚,项和祖.石门水库输水管的加固设计[J].大坝与安全,2005,(1).

