基于改进克隆选择算法的含调整时间并行机调度

牛 群 周台金 王小海 张红运

(上海大学上海市电站自动化技术重点实验室，上海200072)

(上海大学机电工程与自动化学院，上海200072)

并行机调度是生产调度中一类典型的调度问题，近年来受到研究者的广泛关注.已经证明目标函数为最小化最大完工时间即Makespan 最小时，仅有两台机器的并行机调度问题便是NP-hard 问题［1］.在相同并行机的研究中，大多数研究假设工件之间的调整时间(setup time)是可忽略不计的.这种假设能够简化问题模型，便于求解，但在实际的生产条件下，尤其是调整时间依赖于工件加工顺序中的前一个加工工件及工件的分组技术时，调整时间是不可忽略的.研究表明，在生产调度中，若充分考虑调整时间的影响，会使调度模型能更好地解决实际问题，从而为企业降低成本.带调整时间的相同并行机调度问题的研究方法主要包括精确方法和启发式方法.

Lee 等［2］针对该问题，提出了一种三阶段启发式方法.Armentano 等［3］研究了带调整时间的相同并行机调度问题，提出了一种贪婪式随机搜索自适应程序，并且结合基于记忆准则的方法来构造初始种群.何军辉等［4］对含有非常数调整时间的并行机作业排序问题，设计了一种遗传算法的实现形式.

由于精确算法仅适于小规模调度问题，因此智能优化方法被广泛应用于调度问题，如遗传算法、模拟退火等，并取得了良好的效果，由于智能方法简洁、方便、易于实现，因此已成为解决调度问题的一个研究热点.克隆选择是生物免疫系统的重要学说，通过这一概念发展起来的克隆选择算法已经广泛应用于许多优化问题，如旅行商问题、背包问题、电磁优化设计等.克隆选择算法在调度问题中也有应用，Yang 等［5］采用克隆选择算法求解Job Shop调度问题，并结合了局部搜索方法来增强算法的寻优能力.Kumar 等［6］提出了一种新的克隆选择算法来解决连续的flow shop 调度问题.刘晓冰等［7］将免疫克隆选择算法应用于柔性生产调度问题，然后着重设计了克隆免疫算子，最后运用该模型对一个实际生产系统进行仿真调度.

克隆选择算法虽然已经应用于多种优化领域，并取得了显著的效果，但在生产调度方面尤其是对并行机调度问题的研究较少，因此本文采用克隆选择算法来优化带调整时间的并行机调度问题，并针对该调度模型，提出了一种改进的克隆选择算法.该算法采用单机排序的编码方式来代替传统编码方式，从而简化了问题求解;为了能够加快算法搜索性能，提出了一种新的启发式方法来产生初始种群;并且，针对克隆选择算法中重要的变异算子，本文比较了4 种变异方式并给出了分析;最后通过仿真实例进一步验证了改进方法的有效性.

1 含调整时间的并行机调度问题描述

并行机调度问题可以描述为:设有m(m ＞1)台并行机器，需要加工n 个工件，这些并行机的加工性能是完全相同的，每个工件可在任一台机器上完成加工，同时也需要满足以下约束:每台机器在每一时刻只能加工一个工件，一个工件一旦在机器上加工就不能中断，必须要等该工件被加工完成之后，才能加工其他的工件.本文所研究的问题是带调整时间的并行机调度，所谓的调整时间就是指机器i 在加工工件j 完成之后，要进入加工工件k时，中间有一个机器调整时间，只有在机器调整好之后才能加工工件k，所以在计算Makespan 时必须要考虑工件的加工时间和机器的调整时间.设在机器i 上加工的工件排序为π={σ1，σ2，…，σj，…，σk}，则在机器i 上加工的工件σj的开工时间tS(i，σj)和完工时间tC(i，σj)由下面公式计算:

式中，i=1，2，…，m，i 表示机器指针，m 为并行机的机器数;j =1，2，…，k，j 表示工件指针，k 表示在机器i 上待加工工件的数目;pij为第j 个工件在机器i上的加工处理时间;sj1，j2为假设j1，j2在同一台机器上加工时从工件j1转到工件j2的调整时间.

本文的目标函数是最大完成时间的最小化(Makespan)，可由下式表示:

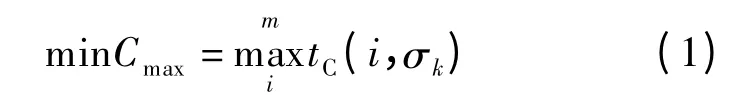
式中，σk表示机器i 上的最后一个被加工的工件.

2 改进的克隆选择算法求解并行机调度

克隆选择算法(clonal selection algorithm，CSA)是基于生物获得性免疫的克隆选择原理［8］而发展起来的一种优化方法，当生物免疫系统遇到抗原入侵时，系统能够快速找到与之相匹配的抗体进行免疫应答，最终消除抗原.由于外界的抗原具有多样性，所以生物免疫系统能够保持抗体的多样性.克隆选择算法根据抗体群体按一定比例数目进行克隆，然后再进行高频变异操作，从而保持了整个群体的多样性.由于该算法操作比较简单，且参数设置较少，因此已经成功应用于许多优化问题.克隆选择算法主要包括3 个操作步骤:克隆复制操作、克隆变异操作和克隆选择操作.

基本的克隆选择算法通过复制多个优秀抗体，然后对这些抗体进行变异产生新的抗体，经过迭代优化找到问题的最优解.因此，该算法寻优性能跟初始种群有关，若初始种群较好，则该算法的求解效率较高.为了提高克隆选择算法的求解性能，本文提出了一种基于单机排序的均匀插入分割点的编码方法以及新的启发式方法的改进克隆选择算法.

2.1 基于单机排序的编码方法

扩展顺序表达方式和分段编码方式能够保证产生的调度方案都是可行解，能够清晰表示每台机器要加工的工件以及工件被加工的顺序，因此这两种编码方式是并行机调度问题常用的2 种编码方式.①扩展顺序表达方式.Cheng 等［9］针对含带调整时间的并行机调度问题提出了一种新的编码方式，即扩展顺序表达方式，首先将n 个工件的编号进行随机全排列，然后随机插入m－1 个分隔符“* ”，这个分隔符是用来区分不同机器上的工件.②分段编码方式.在文献［10］中，将染色体分为两段基因串，每台机器加工的任务代号依次排列作为第一段基因串，每台机器上的任务加工总数作为第一段基因串，则染色体可以表示如下:

其中，Lij表示机器i 上第j 次加工任务的代号;ki表示在机器i 上加工的工件数目;i∈［1，m］，j∈［1，ki］，Lij∈［1，n］，且Lij取互不相同的自然数，因为所有的n个工件必须在m 台机器上加工完，所以

上述2 种编码方式能够保证产生的调度方案都是可行解，但却有较大的随机性，例如10 工件3机器的并行机调度问题，产生的排序为［3 7 2 6 8 4 5 10 9 1］，随机产生的分割点为2 和8，即［3 7 ×2 6 8 4 5 10 ×9 1］，这样势必导致第二台机器加工的工件较多，从而打破了每台机器上的负载平衡，导致了该可行解恶化，因此分割点位置的产生非常关键.考虑到并行机调度问题的特点，希望每台机器上最后一个工件的完工时间比较接近，即每台机器上加工的工件时间越均衡，越有利于得到好的Makespan，因此本文提出了一种新的结合模型特点的编码方式，即单机排序编码方式.首先将n 个工件的编号进行随机排列并放置到单台机器上，如果没有考虑工件之间的调整时间，那么所有可行解中工件的完工时间累加应该是相同的，但是因为考虑了调整时间，因此不同可行解的结果不会相同，每个可行解中n 个工件的加工时间和调整时间总和为T，那么每台机器上期望的加工工件时间为tp=T/m，然后按照pt 进行分段，找到最接近tp的m－1 个分割点.本文提出的这种编码方法与上述1)方法不同之处在于并不随机插入分隔符，而是根据权衡每台机器上总的工件加工时间和调整时间，使分割点尽量均衡，从而更有利于最优Makspan 的求解.

2.2 一种新的启发式方法

一般情况下，在求解优化问题时，初始种群是随机产生的.为了更好地提高算法的收敛能力，本文提出了一种采用启发式方法来产生一部分可行解作为初始种群的方法，该启发式方法是基于单机调度模型提出来的，可以用下面步骤来描述:

①令k=1，n 表示工件的数目.

②判断是否满足停止条件，若满足，跳出循环，否则，进入③.

③以工件k 作为起始的加工工件，然后查询该工件与其他工件之间的调整时间，找到调整时间最小的那个工件作为下一个加工工件.依此类推，直至所有工件均被加工为止.

④令k=k+1，返回②.

2.3 克隆复制操作

本文首先将抗体的亲和度进行排序，将种群中所有抗体由好到坏进行排序，根据抗体在种群中的位置来确定抗体克隆的数目.抗体克隆数目的大小由下式表示:

式中，Nt为第t 个个体被克隆的数目;M 为表示初始种群的规模;β 为个体的克隆规模.

2.4 克隆变异操作

变异操作是克隆选择算法当中最主要的操作，也是保持种群多样性和种群进化的操作.变异方法有很多种，本文采用了文献［11］中的4 种变异方法.

2.5 克隆选择操作

将每个个体经过克隆复制和变异之后的个体与原始个体进行比较，若克隆复制和变异之后的个体比原始个体优，则用变异后的个体替换原来个体进入下一代，否则原始个体进入下一代循环.

2.6 改进的克隆选择算法-HSMCSA

改进的克隆选择算法解决并行机调度问题，主要的改进措施为:采用单机排序编码方式、根据单机调度最优解与随机混合的启发式方法产生初始种群以及根据单机调度模型以及均匀插入分割点来计算种群中每个个体的亲和度.改进的克隆选择算法主要步骤如下:

①根据启发式方法生成一个规模为M 的初始种群pop，并确定各种参数的值.

②计算种群个体的亲和度，根据目标函数来判断个体好坏，将个体从好到坏进行排序，根据个体在种群中的位置来确定个体克隆复制的数目.

③对克隆后的抗体执行变异操作，变异按概率等于1 进行变异.

④重新计算变异后的抗体的亲和度，将初始种群的每个个体与该个体行克隆复制和变异操作得到多个抗体进行比较，选出其中最好的一个抗体进入下一代.

⑤另迭代次数t=t +1，检查是否满足终止条件，若满足，终止迭代，输出最优解;若不满足，则转到②，进行下一个迭代操作.

3 仿真结果及其分析

3.1 四种变异算子的比较

本文所提出的采用单机排序编码方式的克隆选择算法对文献［4］中的2 个算例进行求解比较4种变异操作结果，一个10 工件3 机器，另外一个算例是20 工件5 机器.参数设置如下时:个体的克隆规模β=0.5，变异概率Pm=1，启发式生成的个体占种群规模比例HR=0.5，运行10 次，结果如表1所示，表1中“S”表示种群规模，“Best”表示运行10 次的最好解，“Ave”表示运行10 次的平均解.

从表1中可以看出采用两点互换变异操作比其他三种变异操作所得到的结果优，同时从表1可以看出，用本文所提出的克隆选择算法找到的解要比文献［4］中采用遗传算法找到的解优.

表1 克隆选择算法采用4 种不同变异的结果比较

3.2 启发式方法的仿真结果

为了验证2.2 章节提出的启发式方法的有效性，采用文献［4］中的算例进行仿真，表2给出了不同比例下(HR)的启发式方法产生初始种群的仿真结果，“HR =0”表示初始种群全部随机产生，“HR=0.3”表示初始种群中有30%的个体采用启发式方法生产，70%的个体随机生成.参数的设置:种群规模M =20，最大迭代次数T =1 000，β=0.5，Pm=1，运行20 次.表2中“Best”表示运行20 次中找到的最好解，“Ave”表示运行20 次的平均解，“Worst”表示运行20 次中找到的最差解.

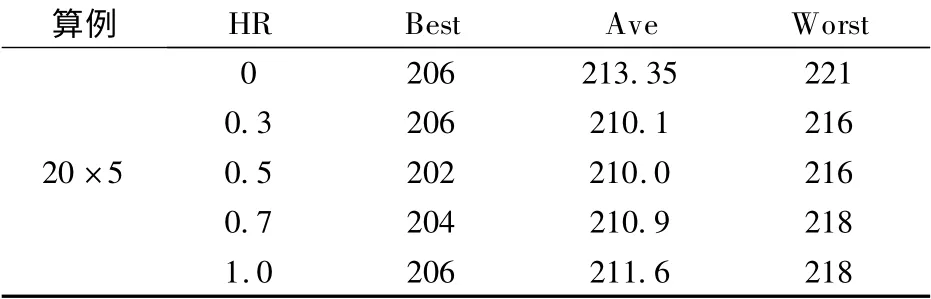
表2 不同比例下启发式方法的结果比较

从表2可以看出，当HR ＞0 时，所有的比例下得到的解均好于HR =0 的情况.这说明加入启发式的方法产生初始种群比随机产生初始种群更加有效.表2同时表明在全部用启发式方法产生初始种群，即HR=1 得到的结果还没有部分用启发式方法产生初始种群的结果要好，说明全部用启发式方法产生初始种群经过迭代容易陷入局部最优，然而在初始种群中加入一些随机产生的解能够增加种群的多样性，克服早熟收敛.从表2的各种比例的对比可以进一步发现当HR =0.5 时，所得结果最优.

3.3 4 种算法的仿真结果

为了进一步验证本文所提出的采用单机排序编码方式的克隆选择算法的有效性，随机生成了24 组算例，共有4 种规模:50 个工件5 台并行机、60 个工件5 台并行机、70 个工件5 台并行机以及80 个工件5 台并行机，每个规模随机生成了6 个算例，工件的加工时间和机器的调整时间是根据均一分布产生，加工时间服从U{1，100}的均一分布，调整时间服从U{1，50}的均一分布.表3当中的“50－5－1”表示50 个工件、5 台并行机规模下的第一个算例.表3表示了这24 组算例的运行结果，其算法的参数选择如下所述:种群规模M =20，最大迭代次数T=1 000，个体的克隆规模β=0.5，变异概率Pm=1，生成的个体占种群规模比例HR =0.5，运行20 次，采用遗传算法(GA)，采用扩展顺序表达方式进行编码的克隆选择算法(CSA)，单机排序编码方式的克隆选择算法(SMCSA)以及50%初始种群由启发式方法产生(HR =0.5)的单机排序编码方式的克隆选择算法(HSMCSA)这4 种算法进行验证这24 组算例.遗传算法(GA)的交叉算子采用的是文献［8］中的交叉算子交叉概率Pc=0.8，变异概率Pm=0.2.本文的采用两点互换的变异方式.同时，表3中“Best”与“Ave”表示的含义与表2相同.由表3的数据分析可得如下结论:

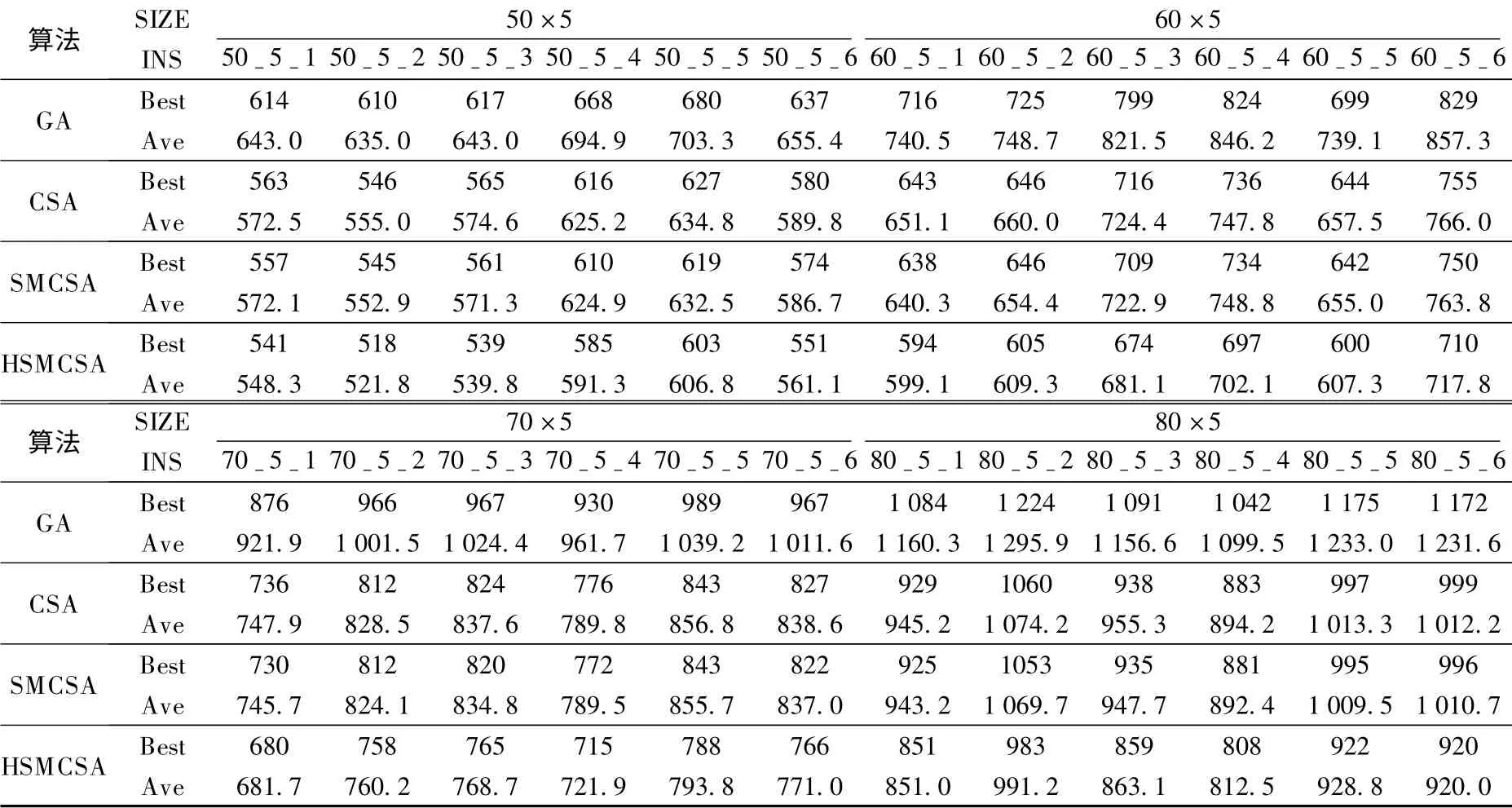
表3 24 组算例的运行结果

1)3 种克隆选择算法(CSA，SMCSA 和HSMCSA)得到的最优解和平均解都要优于遗传算法的解，说明克隆选择算法很适合并行机调度问题的求解.

2)在算例规模小的时候，SMCSA 的解与CSA 的解比较相近，但随着问题规模的增加，SMCSA 的求解性能优于CSA 算法，说明采用单机排序的克隆选择算法比随机编码机制更有优势.

3)HSMCSA 算法得到的结果在4 种算法中最优，通过24 组算例数据的计算可得出，HSMCSA 相比GA 求解性能提高了18.5%，相比CSA 提高了7.2%，相比SMCSA 提高了6.6%.而且，随着算例规模的增大，这种优势更加明显.

4 结语

本文采用了克隆选择算法来求解带调整时间的相同并行机调度问题.针对并行机调度问题，提出了一种基于单机排序的编码方式.为了进一步提高克隆算法的求解性能，提出一种新的启发式方法产生初始种群，即HSMCSA.仿真结果表明，本文所提出的HSMCSA 求解带调整时间的相同并行机调度问题非常有效，在其优化性能上优于本文所提出的其他算法.因此，进一步工作可将HSMCSA 应用于其他车间调度问题中.

References)

［1］Garey M R，Johnson D S.Computers and intractability:a guide to the theory of NP-completeness［M］.San Francisco:Freeman，USA，1979.

［2］Lee Y H，Pinedo M.Scheduling jobs on parallel machines with sequence-dependent setup times［J］.European Journal of Operational Research，1997，100(3):464-474.

［3］Armentano V A，Franca M F.Minimizing total tardiness in parallel machine scheduling with setup times:an adaptive memory-based GRASP approach［J］.European Journal of Operational Research，2007，183(1):100-114.

［4］何军辉，周泓.求解含调整时间并行机排序问题的遗传算法［J］.系统工程理论方法应用，2002，11(4):285-289.

He Junhui，Zhou Hong.A kind of genetic algorithm for solving parallel machine scheduling problems with setup times［J］.Systems Engineering-Theory Methodology Application，2002，11(4):285-289.(in Chinese)

［5］Yang Jinhui，SuLiang N，Lee H P，et al.Clonal selection based memetic algorithm for job shop scheduling problems［J］.Journal of Bionic Engineering，2008，5(2):111-119.

［6］Kumar A，Prakash A，Shankar R，et al.Psycho-clonal algorithm based approach to solve continuous flow shop scheduling problem［J］.Expert Systems with Applications，2006，31(3):504-514.

［7］刘晓冰，吕强.免疫克隆选择算法求解柔性生产调度问题［J］.控制与决策，2008，23(7):781-785.

Liu Xiaobing，Lü Qiang.Immune clonal selection algorithm for flexible job-shop scheduling problem［J］.Control and Decision，2008，23(7):781-785.(in Chinese)

［8］Castro L N，Zuben F J.Learning and optimization using the clonal selection principle［J］.IEEE Trans on Evolutionary Computation，2002，6(3):239-251.

［9］Cheng Runwei，Gen M.Parallel machine scheduling problems using memetic algorithms［J］.Computers and Industrial Engineering，1997，33(3/4):761-764.

［10］刘民，吴澄.进化规划方法在最小化拖期任务数并行机调度问题中的应用［J］.电子学报，1999，27(7):132-134.

Liu Min，Wu Cheng.Application of evolutionary programming method in parallel machine scheduling problem of minimizing the number of tardy jobs［J］.Actaelectronica Sinica，1999，27(7):132-134.(in Chinese)

［11］Eiben A E，Smith J E.Introduction to evolutionary computing［M］.Springer，2007.