改进的快速复值FastICA算法研究
赵立权,于轼群
(1.东北电力大学信息工程学院,吉林吉林132012;2.中国联通哈尔滨分公司,哈尔滨150001)
独立分量分析(Independent Component Analysis,ICA)是解决盲源分离问题的主要方法之一,它仅利用信源信号非高斯相互统计独立的假设条件,从接收到的混合信号中估计出信源信号。复值ICA算法是针对复值域信号的一种新的信号处理方法,目前主要应用于盲解卷积、无线通信、功能性核磁图像处理、阵列信号处理等方面[1-4]。随着ICA算法理论的逐渐发展和成熟,近些年来,复值ICA算法受到了越来越多学者的广泛关注,涌现出许多优秀的算法[3-11]。复值快速独立分量分析(Fast Independent Component Analysis,FastICA)一种典型的批处理固定点复值ICA算法[5],后来的许多复值ICA算法都是在它的基础之上发展起来的,典型的改进算法就是基于Huber M估计函数的复值ICA算法[7],该算法相对原算法性能更好,为了进一步提高算法的性能,本文从复值ICA代价函数所采用的非线性函数角度出发,对稳健性更好Tukey双权函数进行修正后作为代价函数的非线性函数,推导出运算速度更快的改进的复值ICA算法。
1 复值ICA数学模型
复值ICA的基本数学模型如下:

ICA的基本假设条件只是为了保证ICA算法有解,但是毕竟信源信号S和混合矩阵A都未知,因此通过ICA算法得到的信源信号的估计Y相对信源信号S存在一定的不确定性。例如式(1)可以写成如下形式:
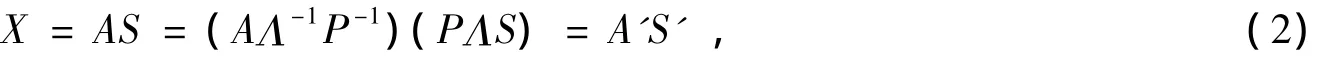
式中:Λ=diag(a1ejθ1,a1ejθ2,…,anejθn),an和θn为任意不为零的值;Λ-1是Λ的逆矩阵;P是任意可逆的单位置换矩阵;P-1是P的逆矩阵。矩阵Λ和P是任意的,那么得到A'=AΛ-1P-1和S'=PΛS也是任意的,但是A'S'得到的混合信号X是固定的,所以复值ICA对接收到的信号X进行分离,得到的对信源信号的估计信号可能是S'或者S,S'和S的幅度、相位和顺序不一样,因此产生了复值ICA对信源信号估计的不确定性。在ICA研究中,人们更多关注的是信号的波形,只要分离信号和信源信号的波形一样,就认为算法是有效的。
2 复值FastICA算法
复值FastICA算法是由赫尔辛基工业大学的Bingham和Hyvärine仿照实值FastICA算法,提出的一种经典的针对复数信号ICA算法[5]。该算法是一种批处理的固定点迭代算法,算法不需要设置学习速率,收敛速度快。
复值FastICA算法和其它批处理ICA方法一样,都需要对接收数据进行预处理。设n维接收信号X=[x1,x2,…,xn]T,为了简便,假设接收信号X经过预处理后得到的白化信号为Z=BX,B为白化矩阵。对于白化后的信号的盲分离,复值FastICA算法选择“自下而上”的ICA方法构造代价函数,在代价函数中采用非线性函数近似高阶统计量。其代价函数定义为:

式中:G为非线性函数;W=[w1,w2,…,wn]T为n维的复值分离向量;Z为白化后的信号满足E{ZZH}=I。在复值独立分量分析中一般假设信源信号的幅值为1,WHZ是对信源信号的估计,因此也应满足幅值为1的条件,即E{WHZ2}=E{WHZZHW}=WHW=1,W满足归一化条件。
在E{WHZ2}=WHW=I的约束条件下,复值FastICA算法代价函数为:

式中:β为拉格朗日乘子;采用牛顿迭代算法对代价函数式(4)进行优化,得到分离向量的迭代公式:
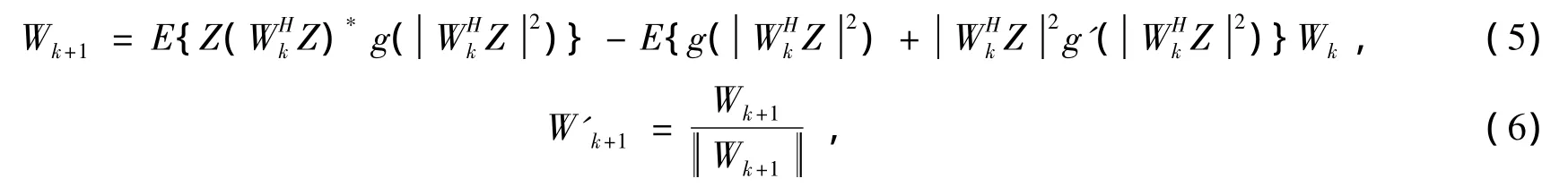
式中:g是G的导数,g'是g的导数。可选择的三种非线性函数的具体表示式如下[5]:
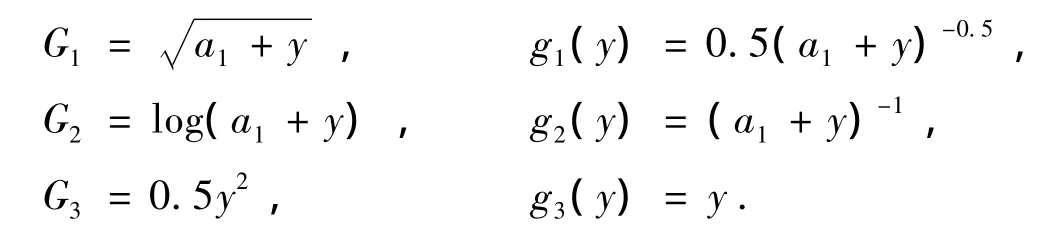
3 改进的复值FastICA算法
复值FastICA算法的稳健性好坏取决于所采用的非线性函数,为了提高算法性能,文献[7]提出了一种改进的复值FastICA算法,该算法采用Huber M估计函数作为代价函数中的非线性函数,相对原FastICA算法稳健性更好。其所采用的Huber M估计函数及其一、二阶导数表达式如下:


虽然文献[7]中采用的非线性函数结构简单,但是由于其二阶导数中存在求矩阵的逆,即“u-3/2”项,工程上实现矩阵逆运算比较复杂,而且增加了计算量。
为了避免矩阵求逆运算,减少计算量,提高算法运算速度,本文采用Tukey函数作为代价函数中的非线性函数[12]。在式(3)和式(5)式中,非线性函数均以估计函数的平方作为变量,为此本文对Tukey函数进行修正,将原变量看作是修正后变量的平方,即修正后的Tukey函数为
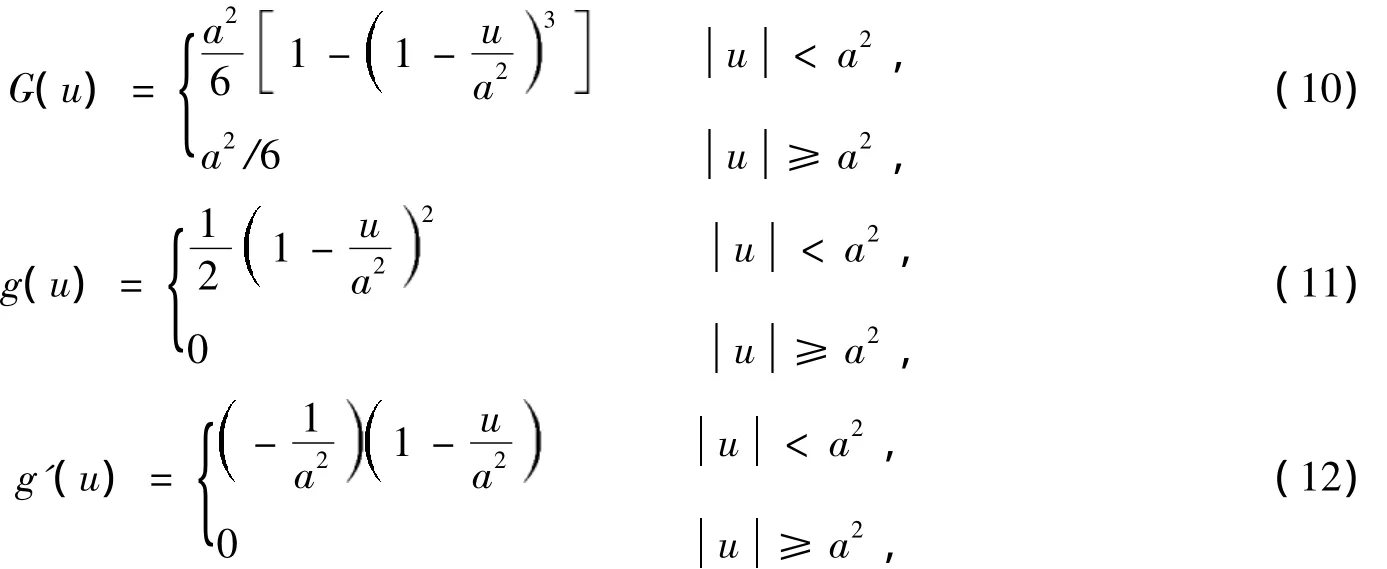
其中:g(u)和g'(u)分别为G(u)的一阶和二阶导数。从上式数学表达式可以看出,修正后的Tukey函数的导数不含有矩阵求逆运算,因此减少了计算量。
图1是Tukey函数和Huber函数及其一阶和二阶导数,其中Tukey函数阈值a=2,Huber函数阈值θ=0.9(文献[7]中取θ=0.9性能比较理想)。从图中可以看出,Tukey函数及其导数在超过阈值后为常数,因此对超过阈值的奇异值点有较好抑制性。而Huber函数超过阈值后为直线,因此对奇异值点抑制性能较差。

图1 非线性函数及其导数
4 实验仿真和结果分析
实验仿真中,采用独立分量分析算法中常用的
性能指标(Performance Index,PI)作为评价函数,用来度量算法误差大小的标准,其具体表达式如下:
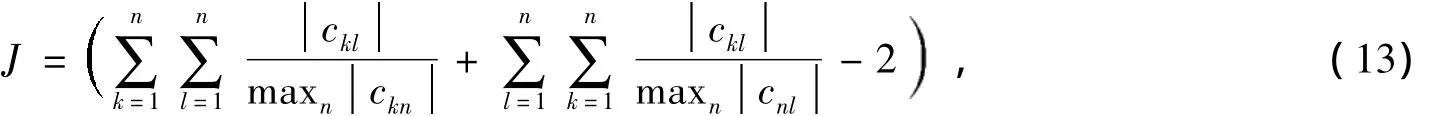
式中:C=WHBA,W是白化后信号的分离矩阵,B是白化信号,A是混合矩阵。性能指标J的取值越小,表示分离误差越小。
实验1验证算法的有效性。
信源信号为一个exp(j100πt)、一个BPSK信号和一个QAM信号,采样点为1 000点,随机产生复值混合矩阵A为:


图2 信源信号
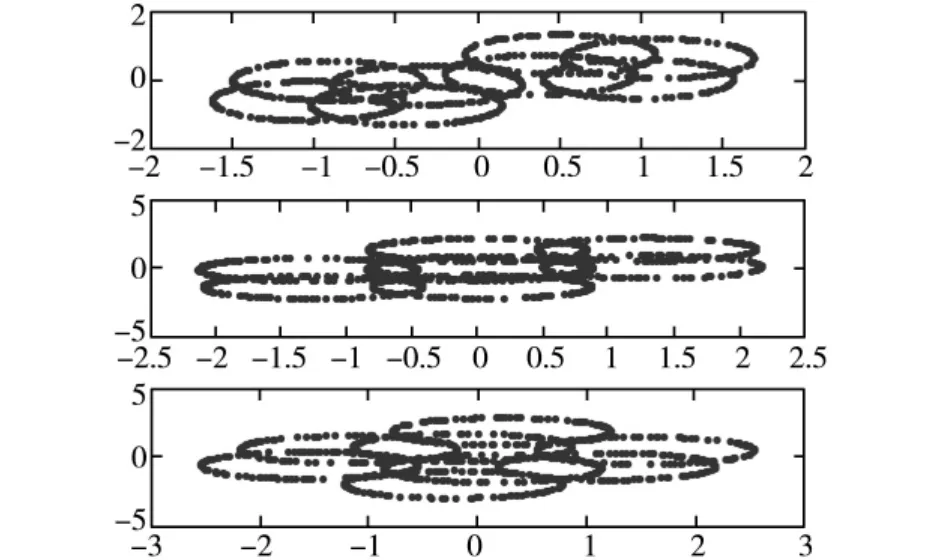
图3 复值混合信号
图2是信源信号的波形图,图3是混合信号,图4是从复值混合信号中分离出的信号,即信源信号的估计信号。图4第一个图和图2的第二个图对应、图4的第二个图和图2的第三个图对应、图4的第三个图和图2的第一图对应。对比图4和图2可以看出,分离信号和信源信号波形基本一样,证明了算法的是有效的,同时二者之间存在顺序、相位的不确定性,该不确定性是复值ICA固有不确定性,通过进一步处理后并不影响实际应用。

图4 信源信号的估计信号
实验2验证算法的性能。
为了从统计角度验证算法的性能,在实验1信源信号的基础上,进行1 000次运算取平均值,每次运算的复值混合矩阵都随机产生,其中基于Huber函数的FastICA算法门限值取θ=0.9,原FastICA算法采用G1(y)=(a+y)0.5,因为文献[7]仿真证明此时这个两种算法性能比较好。本文提出的基于Tukey函数的FastICA算法门限取。
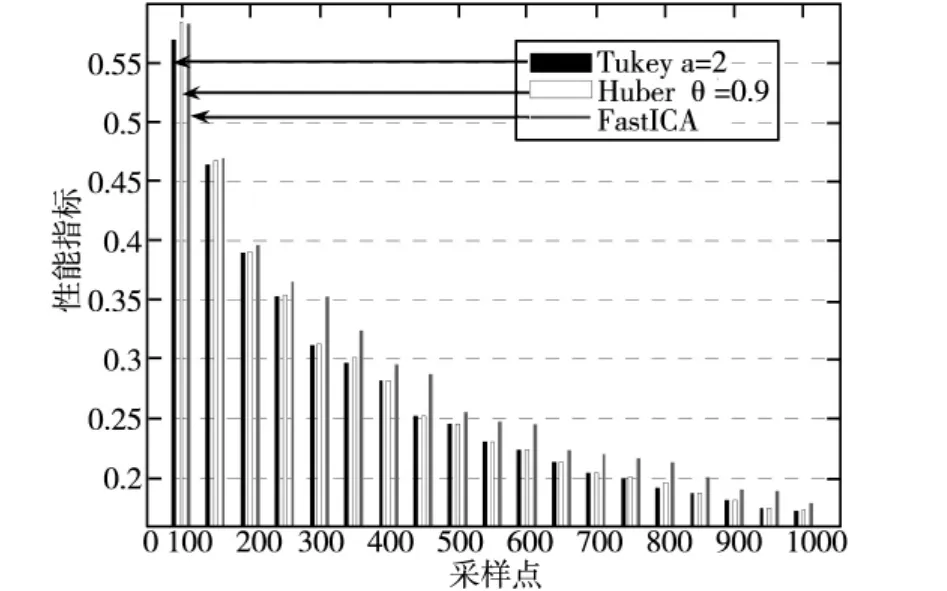
图5 采样与性能指标直方图

图6 采样点与运行时间关系曲线
图5是采样点与性能指标关系直方图。从图中可以看出,在较低采样点时本文提出基于Tukey函数的复值ICA算法误差新能要好于其它算法,但是随着采样点数量的增加,本文算法误差性能与基于Huber函数的复值ICA算法基本一样,但是始终都比原FastICA算法性能要好。
图6是得到图5性能时算法收敛所需的平均运行时间与采样点关系曲线,从曲线可以看出三种算法中,本文算法的运行时间最短,证明了本文算法的计算量小。综合图5和图6可得,本文算法误差性能与基于Huber函数的复值ICA算法性能相当,但是比其运行时间短,也就是计算量小。而且在低采样时,本文算法误差最小。
4 结束语
本文在复值FastICA算法的基础上,提出了一种改进的复值FastICA算法。本文算法误差性能好于原复值FastICA算法,与基于Huber函数的复值ICA算法相比,本文算法在采样点较少时误差性能更好,大采样点时基本一样,但是本文算的运算时间明显小于原FastICA算法及基于Huber函数的复值ICA算法,即本文算法的计算量更小。
[1]H Li,M Correa.Application of Independent component analysis with adaptive density model to complex-valued FMRI data[J].IEEE Transactions on biomedical engineering,2011,58(10):2794-2803.
[2]L Wang,H Ding,F Yin.Combining superdirective beamforming and frequency-domain blind source separation for highly reverberant signals[J].EURASIP Journal on Audio,Speech,and Music Processing,2010(1):1-13.
[3]H shen,M Kleinsteuber.Complex blind source separation via simultaneous strong uncorrelating transform[C].LVA/ICA'10 Proceedings of the 9th international conference on Latent variable analysis and signal separation.Belin Heidelberg,2010:287-294.
[4]付卫红,杨小牛,刘乃安,等.通信侦查中通信复信号的盲源分离算法[J].四川大学学报,2008,40(1):118-121.
[5]E Bingham,E Hyvarinen.A fast fixed-point algorithm for independent component analysis of complex valued signals[J].Internation Journal of Neural Neural Systems,2000,10(1):1-8.
[6]Eriksson J,Koivunen V.Complex random vectors and ICA models:identifiability,uniqueness,and separability[J].IEEE Transactions on Information Theory,2006,52(3):1017-1029.
[7]C Jih-cheng,S Douglas.A Robust complex FastICA algorithm using the Huber M-Estimator Cost function[C].ICA2007,UK,London,2007:152-160.
[8]S Javidi,P Mandic.Complex blind source extraction form noisy mixtures using second-order statistics[J].IEEE transaction on circuits and systems,2010,57(7):1404-1416.
[9]Novey M.Adali T.Complex ICA by Negentropy Maximization.Neural Networks[J].IEEE Transactions on neural networks,2008,19(4):596-609.
[10]付卫红,杨小牛,刘乃安,等.基于变步长最优化的EASI盲源分离算法[J].四川大学学报,2008,40(1):118-121.
[11]林秋华,李镜.基于ICA-R的复值信号抽取方法[J].大连理工大学学报,2008,48(6):919-925.
[12]A Asad,F Muhammad.A modified m-estimator for the detection of outliers[J].PJSOR,2005,1(1):49-64.

