中能重离子核反应中椭圆流与横向速度的关联

颜廷志

(东北电力大学能源与动力工程学院，吉林吉林132012)

各向异性流是研究中能重离子碰撞动力学的一条有效途径。在理论和实验上都取得了不少成果，尤其是定向流(v1)和椭圆流(v2)对碰撞能量、碰撞系统、同位旋、碰撞参数等的依赖性研究进一步加深了对集体流的产生和性质的认识［1－3］。中能重离子碰撞是火球膨胀、集体转动、旁观者遮挡、库仑排斥等因素的共同作用，因此所形成的椭圆流也是复杂的。与横向半径相关的横向速度能够反映核碎片所处坐标空间与动量空间的关联，揭示核碎片在横向半径方向的受力情况。本文用同位旋相关的量子分子动力学(IQMD)模型模拟碰撞能量为25 MeV/A、3～5 fm碰撞参数区间的64Cu+64Cu核反应，通过对轻碎片(质量数A≤2)在平面和出平面横向速度的比较，能够较好反映椭圆流与横向半径之间的关系。

对粒子的方位角分布进行傅立叶展开可得到:

椭圆流通常被认为主要是由于核碰撞重叠区域各项异性的压力梯度造成的，因此携带动量空间和坐标空间的关联信息。横向速度也包含坐标空间和动量空间的信息，通常定义为。其中rt、p0分别为碎片的横向位置和总动量大小。

1 IQMD模型

中能区重离子碰撞是吸引的平均场和排斥的核子－核子碰撞相互竞争的过程，泡利阻塞效应也十分显著。因此对于非对称碰撞系统这几个方面的同位旋效应需要考虑。本文采用的模型是同位旋相关的量子分子动力学(IQMD)模型。它是一种多体核子输运理论模型，是在QMD模型的基础上发展起来的，主要包括以下几个主要部分:靶和炮弹核子的初始化、核子在相互作用平均场和两体碰撞作用下的演化、泡利阻塞效应等，并考虑了这几个方面的同位旋效应，即在处理过程当中严格区分了中子和质子。该模型能较好地描述从十几MeV/A到2GeV/A能量范围内的重离子碰撞中的碎片形成、动力学涨落及原子核多重碎裂等现象。关于QMD理论模型的详细阐述可参见文献［4］。

在IQMD模型中，核平均场通常表示为

其中:ρ0是正常核物质密度(0.16 fm－3);ρn、ρp、ρ分别是中子、质子和总的密度;τz是同位旋自由度的z分量，对中子等于1，对质子等于－1。系数α、β和γ是核状态方程的势参数，Csym是由于核物质中子和质子密度差引起的对称能项系数，一般取Csym=32 MeV。Vc是库仑势能，UYuk是表面能。本文取α=124 MeV，β=70.5 MeV，γ=2，核物质不可压缩系数K=380 MeV，即所谓的硬核状态方程势参数。

2 模拟结果和讨论

用硬核状态方程参数的IQMD模型模拟了碰撞能量为25 MeV/A、碰撞参数b在3～5 fm范围的64Cu+64Cu核反应，共模拟了100 000个核反应事件。物理结果是针对200 fm/c时刻、快度在－0.5～0.5范围、质量数A≤2的轻碎片提取的，这样的碎片其椭圆流更加敏感。

图1给出了200 fm/c时刻质量数A≤2的轻碎片的平均横向速度βt与横向半径rt的关系。从图1可以看出，横向速度随横向半径增加而单调增加。这与相对论能区的结果［5］相似，但两者的机制有所不同。在相对论能区，横向流的形成主要是由于核物质重叠区域的强大的压力梯度导致的，核碎片受到的库仑斥力基本可以忽略，所以当核碎片飞行越来越远离重叠区域，所受到的合力越来越弱，横向速度随着横向半径的增加越来越慢，故而逐渐趋于平衡。而中能区的核碰撞是平均场和核子－核子碰撞的共同作用，长程的库仑斥力也不能忽略，所以当核碎片飞行越来越远离重叠区域，平均场和核子－核子碰撞的作用逐渐可忽略，但长程的库仑斥力依然不能忽略，故核碎片的横向速度随横向半径增大而逐渐增大。只有当核碎片远离足够距离而库仑斥力足够小时，横向速度才不会再增加而趋于最大的平衡值。从图1也可看出，当横向半径rt足够大时，横向速度βt有趋于平衡的趋势。

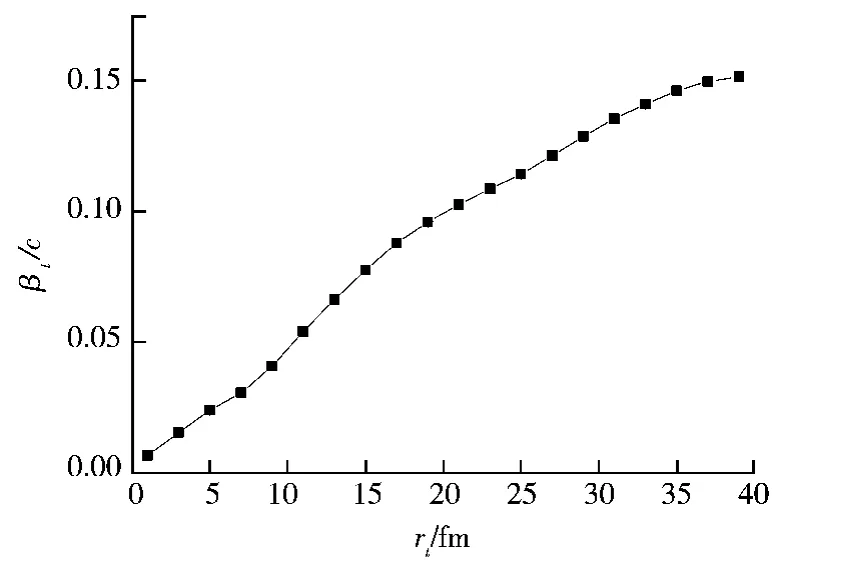
图1200 fm/c时刻质量数A≤2的轻碎片的横向速度βt与横向半径rt的关系

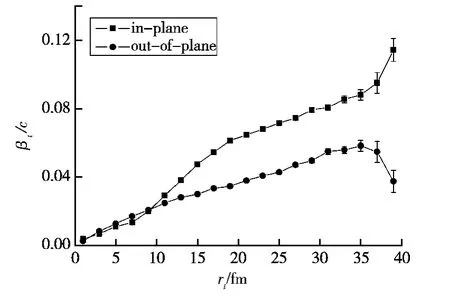
图2200 fm/c时刻质量数A≤2的轻碎片的在平面(方块)和出平面(圆点)横向速度与横向半径的关系

图2为200 fm/c时刻质量数A≤2的轻碎片的在平面横向速度(记为βt－in)和出平面横向速度(记为βt－out)与横向半径的关系。在平面横向速度和出平面横向速度分别用为方块和圆点图标，分别是横向速度在反应平面内和反应平面外的分量。它们随横向半径变化的趋势是相似的，即都随横向半径的增加而增加;但是在大约rt＜10 fm内出平面横向速度大于在平面横向速度，而在rt＞10 fm后出平面横向速度反而小于在平面横向速度，且不同横向半径处在平面横向速度和出平面横向速度的增加速率也不同。如果出平面横向速度比在平面横向速度增加的快，说明核碎片出平面方向受到的斥力大于在平面方向受到的斥力。因此为了研究核碎片的受力变化，有必要对在平面横向速度和出平面横向速度做差值，故而引入。

图3给出了该差值δβt与横向半径之间的关系。可以看出，在大约rt＜7 fm范围内，δβt为负值，且随着横向半径增加而下降，这说明在平面横向速度增加比出平面横向速度增加慢，即核碎片在出平面方向受到的斥力要大于在平面方向受到的斥力。故核碎片的发射越来越倾向于出平面，即出平面发射的核碎片越来越多，在平面发射的核碎片越来越少，那么就会表现于椭圆流v2上，v2应该随着横向半径的增加而减小。正与图4所示的椭圆流随横向半径变化曲线一致，在rt＜7 fm范围内椭圆流v2随着横向半径的增加而减小。随着横向半径的继续增加，δβt仍为负值，但趋势改为增加，说明在平面横向速度增加比出平面横向速度增加快，核碎片在平面方向受到的斥力要大于出平面方向受到的斥力，但出平面横向速度仍大于在平面横向速度，故在平面发射的核碎片的数目仍在减小，直至出平面横向速度等于在平面横向速度时，即在δβt=0时，在平面发射的核碎片数目达到最少，椭圆流v2应该达到最小值。图3中δβt=0时，rt≈10 fm，而图4中椭圆流v2达到最小值时，rt≈10 fm，可见两者一致。随着横向半径的继续增加，δβt为正值，趋势仍为增加，说明在平面横向速度比出平面横向速度大，且增加得也快，核碎片在平面方向受到的斥力仍大于出平面方向受到的斥力，则在平面发射的核碎片的数目在增加，椭圆流v2应该也随着横向半径增大而增大，如图4所示。直至δβt达到饱和时(如图3所示)，核碎片在平面方向受到的斥力等于出平面方向受到的斥力，则在平面发射的核碎片的数目应该达到最大饱和值，正如图4所示。由以上分析可见，通过引入δβt，即在平面横向速度和出平面横向速度的差值，可以很好的理解、印证椭圆流随横向半径变化的关系。

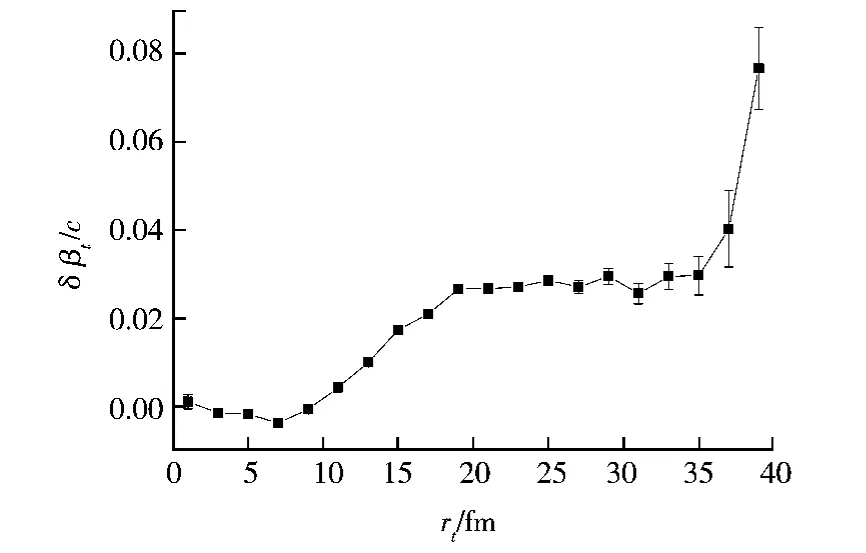
图3 在平面横向速度和出平面横向速度的差值与横向半径的关系

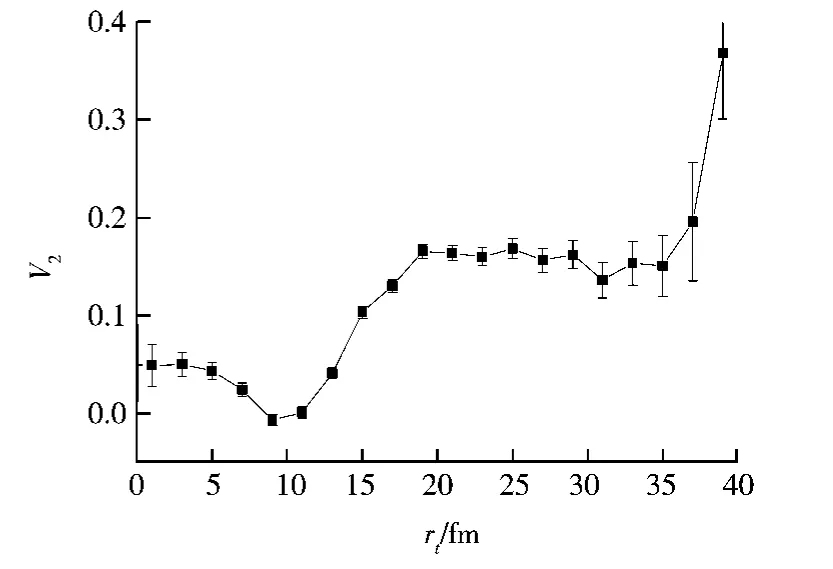
图4 椭圆流v2与横向半径的关系

3 结论

本文用IQMD模型模拟了碰撞能量为25 MeV/A、碰撞参数在3～5 fm范围的64Cu+64Cu核反应，通过对中快度区间、质量数A≤2的轻碎片物理信息的分析，发现通过引入在平面横向动量和出平面横向动量的差值，即δβt=βt－in－βt－out，能够定性地理解核碎片在不同横向半径处的受力变化，并能与椭圆流随横向半径的变化相互印证。这也说明，δβt也可以作为研究核反应动力学的一个探针。

［1］Zheng Y M，Ko C M，Li B A et al.Elliptic flow in heavy-ion collisions near the balance energy［J］.Phys.Rev.Lett.，1999，83:2534－2536.

［2］Perslam D，Gale C.Elliptic flow in intermediate energy heavy ion collisions and in-medium effects［J］.Phys.Rev.C，2002，65:064611－064618.

［3］Yan T Z，Ma Y G，Cai X Z et al.Scaling of anisotropic flow and momentum space densities for light particles in intermediate energy heavy ion collisions［J］.Phys.Lett.B，2006，638:50－54.

［4］Aichelin J.“Quantum”molecular dynamics［J］.Phys.Rep.，1991，202:233－360.

［5］冯启春，张景波，霍雷，张卫宁.RHIC能区Au+Au碰撞中椭圆流的横半径依赖［J］.高能物理与核物理，2006，30(7):633－637.