基于连续时间状态的资产配置优化组合及其选择

姜葵

（湖南涉外经济学院 商学部，长沙 410205）

0 引言

在资本市场上成熟的国家与地区，机构投资者正在日益崛起，机构投资者的资产配置也成为该类投资者面临的一个重要问题。在我国资本市场经历了由无到有、单一到多层次、由小到大的成长过程，目前资本市场已经B股、A股、中小企业板、期货、创业板、外汇及黄金等多个层次的交易市场。但是我国资本市场发展毕竟只有30年的历史，资本市场很多制度还不够完善，而且在筹建时留下了很多缺陷，而且很多资产配置或者投资组合选择的分析方法局限于技术分析、趋势分析及价值分析等传统定性投资组合选择分析，资产配置局限于投资者或者机构投资者的经验及个人能力，导致了资本配置的实效。随投资组合选择理论的不断发展，认识到传统的投资组合选择理论与具有摩擦的现实资本市场条件不相符，所以发展了现代的量化投资组合选择或者资产配置理论，以严谨数值分析、统计计量及信息技术为分析工具，通过具有强大数据处理能力的计算机分析，来对现实资本市场中市场行为、分红、税收、宏观数据等全方位扫描，根据数据或资本市场的变化调整资产配置，来提高资产配置效率。本文就是在这样的背景下，结合目前投资组合选择的均值—方差分析框架，发展了连续时间摩擦环境下的均值—方差资产配置模型。

本文以Zhou&Li(2000)利用随机LQ控制分析框架研究了理想完全市场下的连续时间资产配置选择模型为基础，构建不完全资本市场条件下（考虑了税收、分红及通货膨胀）的连续时间资产配置选择模型，并给出资产配置的最优策略及有效前沿边界。

1 摩擦市场下投资组合选择假定

在有摩擦的资本市场中交易金融资产，必然要考虑通货膨胀、分红及税收等影响交易的因素，并且每一种因素都有一种行为过程：

（1）通货膨胀q() t的行为过程满足常微分方程形式：

单位时间的通货膨胀率用θ(t)来表示。

（2）在时间t到（t+dt）的时间过程中，金融资产的分红为di(t)，税收征收率为α(t)，则在交易过程中两者支付分别为：

由于金融市场是一个有摩擦的市场，资产的真实价格必然受到通货膨胀的影响，根据实际价格与名义价格之间关系，金融资产的实际价值为，即：

通过伊藤引理展开：

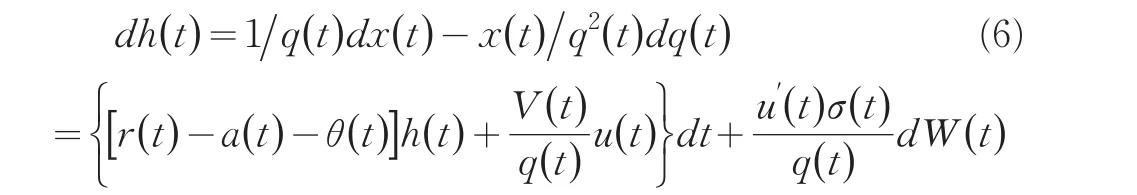
在通货膨胀影响下，金融资产的实际价值如下：

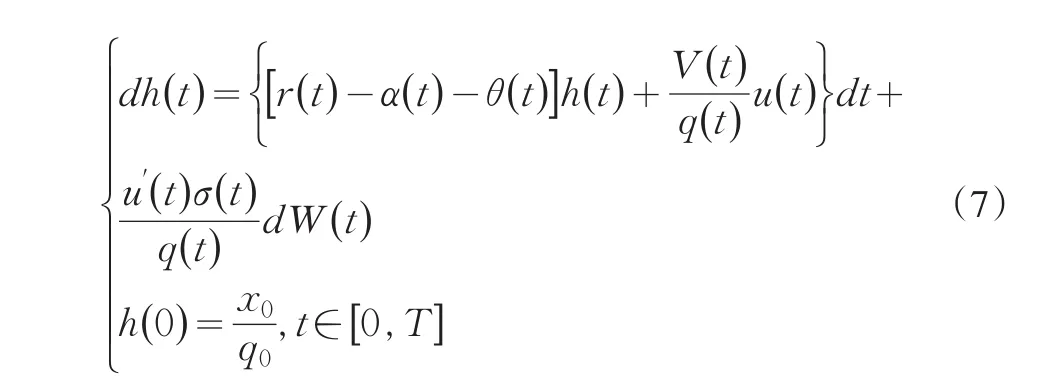
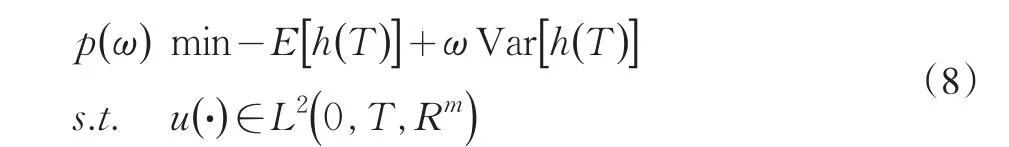
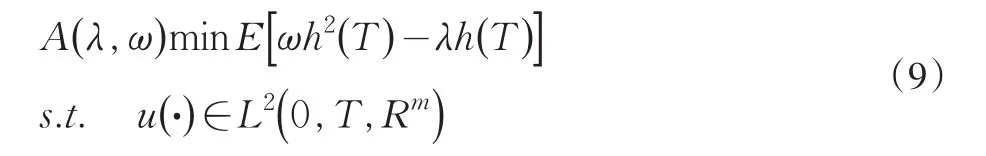
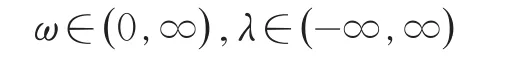
2 嵌入法下利用LQ最优控制理论的目标规划求解

在LQ最优控制下，微分方程变为：

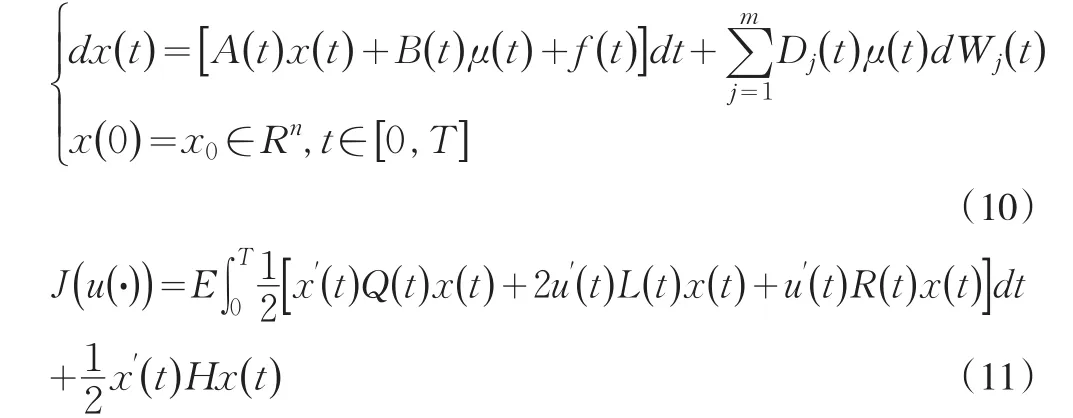
在以上方程条件下，分别考虑Riccaati及常微分方程：（13）

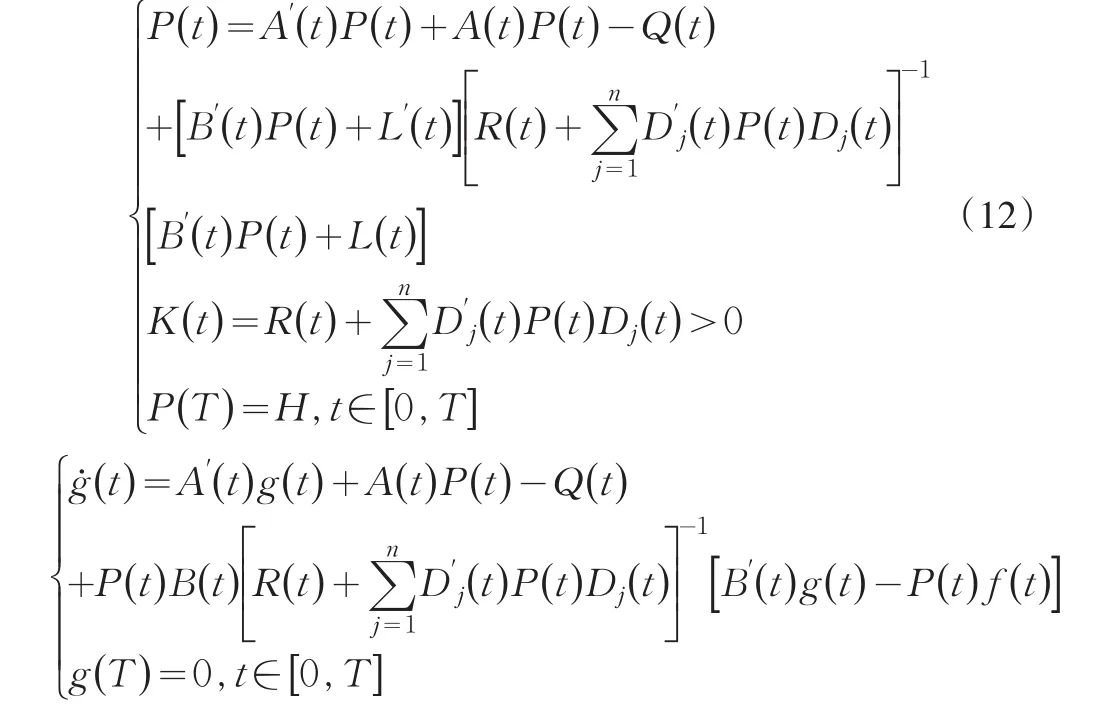
从方程（12）和方程（13）中获得LQ的多目标最优反馈问题解：

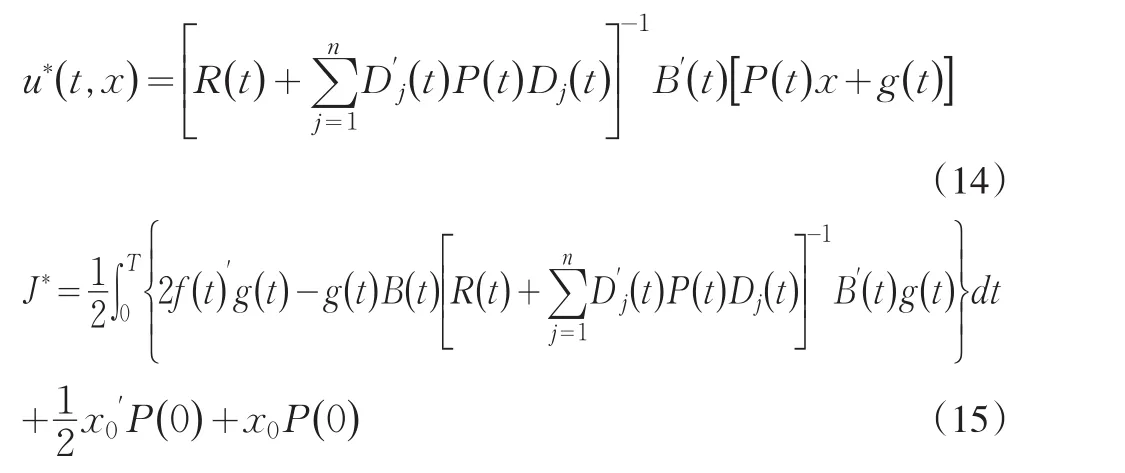
根据方程（14）和方程（15）可以求解A( ) λ,ω的最优解：

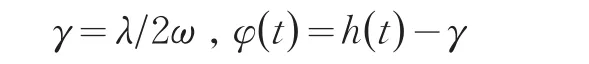
这样就获得以下方程：

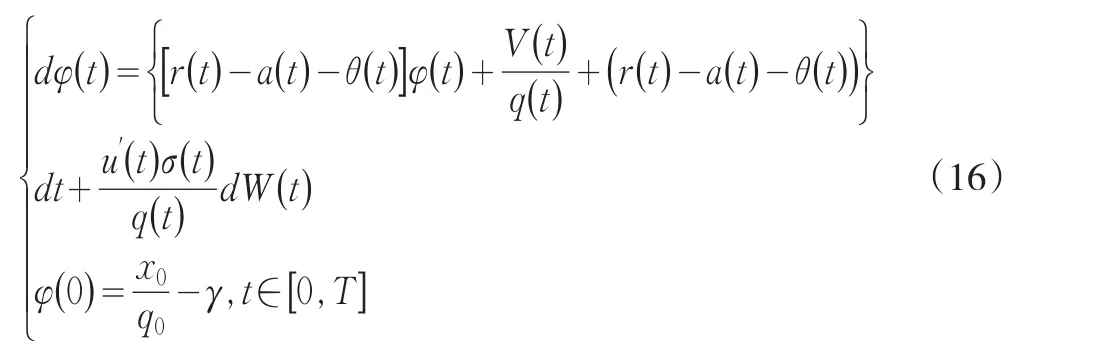
这样方程（16）变为：

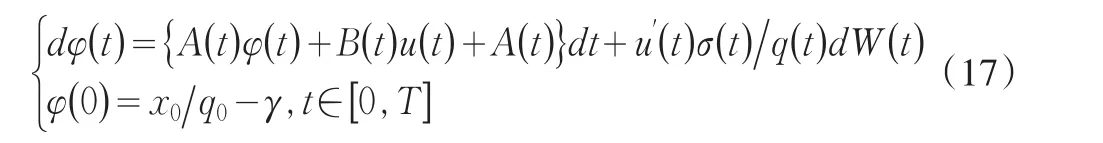
又由于：

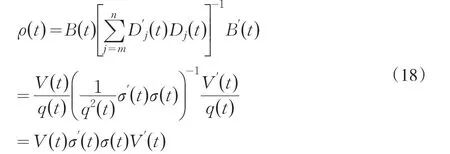
这样方程（12）和方程（13）分别变为：

方程(19)的解为：

方程（2）的解为：

将方程（19）和方程（20）代入上述方程就可得：

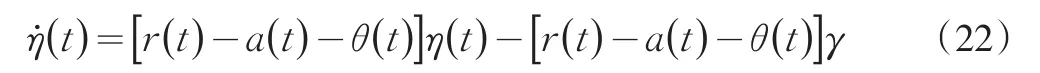
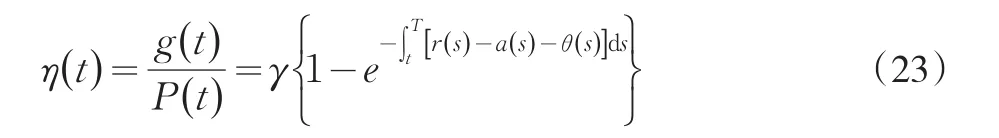
把方程（22）带入到方程（23）中，可得：

3 投资组合的有效前沿边界

将方程（24）带入到方程（7）中，可得：

利用伊藤引理展开可得：

对方程（25）与（26）取期望值，分别可得：

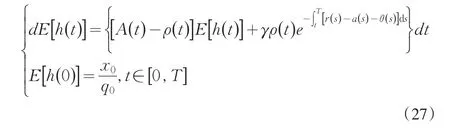
通过最优控制可以化简方程（27）和方程（28）：

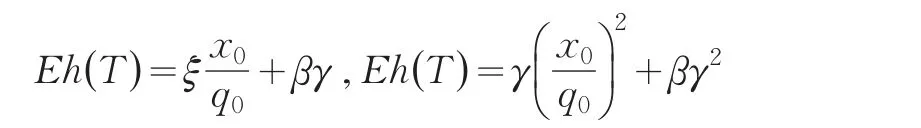
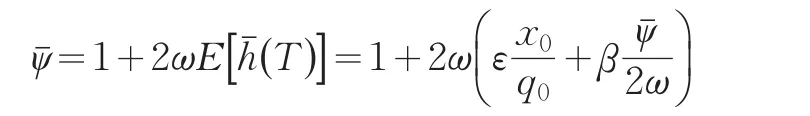
从而得到：

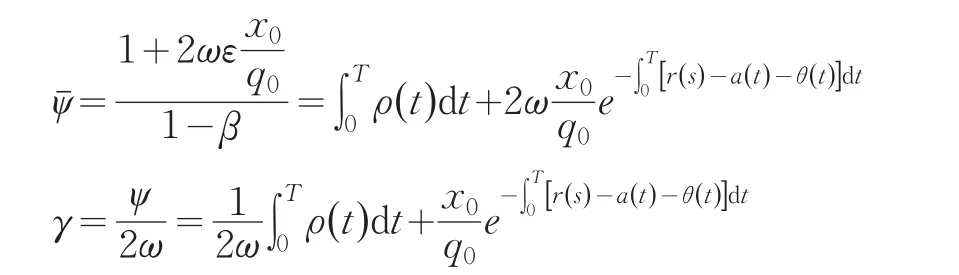
通过以上参数刻画，最优投资组合为：

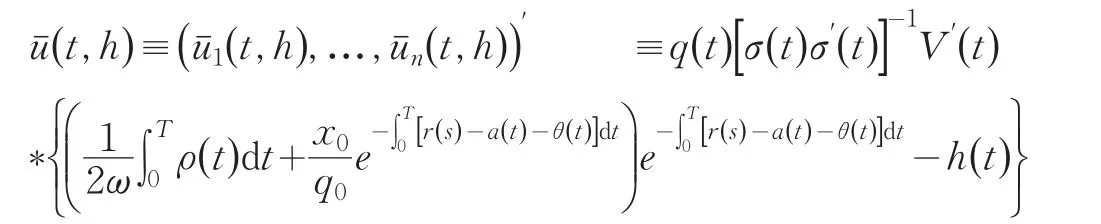
根据参数ψ，γ的最优值，可得投资组合的有效边界前沿：

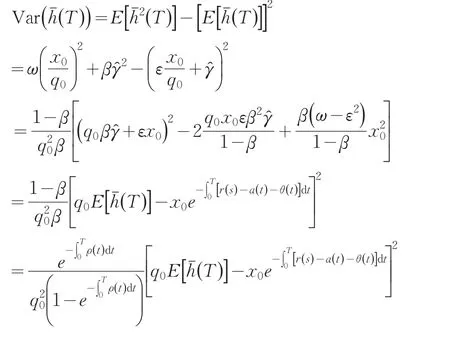
4 结论及启示

论文通过分析资产配置的均值-方差投资组合分析，在考虑了税收、分红等现实摩擦条件下，构建了资本市场的连续时间资产配置模型，并且通过嵌入方法将多目标的资产配置转换成LQ的最优控制分析，获得了资产配置的投资最优策略与有效前沿解。连续时间下的多目标资产配置于传统的均值方差差异在于：考虑了摩擦条件下的连续时间资产配置，建立了一个反映资产配置的各摩擦因素之间相关关系，并且规定风险厌恶程度因子。所以该模型可以反映资本市场投资者特别是机构投资者资产配置的波动现状，而且可以让机构投资者在任何时间改变资产配置策略，为随机摩擦市场环境下资产配置问题提供了理论指导意义。但是如果让资产配置具有更高效率，必须消除资本市场模型，改善资产配置的有效边界前沿：

（1）资本市场上，机构投资者进行金融资产配置决策时，考虑到市场通货膨胀与贴现率风险的影响，在资产配置时必须考虑通货膨胀条件下资产配置的收益曲线斜率或资本市场分布变化时，调整资产配置期限或资产配置的行业类别，以此为基础进行资产配置比例设置，同时尽量在资产配置中用消除了通货膨胀率的实际收益率来计算资产配置收益率。

（2）从模型可以看出，为了获得有效边界前沿必须减少资本市场的摩擦，这必须规范投资者的资产配置，提高资产配置的透明度。在我国资本市场上由于很多政策不完善或者监管不力，由于投资双方的信息非对称性使得资产信息披露的不规范，导致机构投资者利用自己强大信息网络来编造虚假信息。为了规避这种投机行为，资本市场上必须培育合格的审计师事务所、会计师事务所及律师事务所等中介机构，通过这些中介机构来强化上市公司的财务监督，从而让机构投资者不法通过信息非对称来来编制虚假信息，从而降低资本市场摩擦。

[1]Rockafellar.Optimization Conditional Value-at-risk[J].Journal of Risk, 2000,(2).

[2]Deng.A Minimax Portfolio Selection Strategy with Equilibrium[J].Euro⁃pean Journal of Operational Research,2005,(166).

[3]Mossin.Optimal Multi Period Portfolio Selection Policies[J].Journal of Business,1969,(41).

[4]Yuan Rongli.Mutual Funds’Ownership and Frm Performance:Evidence from China[J].Journal of Banking&Finance,2008,32(8).

[5]Wu Song.A Note on a Minimax Rule for Portfolio Selection and Equilib⁃rium Price System[J].APPlied Mathematics and Computation,2009, (208).

[6]Li.Optimal Dynamic Portfolio Selection:Multi-Period Mean-variance Formulation[J].Mathematlcal Finance,2000,(10).

[7]Canakoglu.Portfolio Selection in Stochastic Markets with HARA Utility Functions[J].Eurapean Journal of Operational Research,2010,(201).

[8]蔡晓钮,王明好.新增K种资产与前n种不相关时证券组合前沿的漂移问题[J].系统工程理论方法应用,2003,12(4).

[9]吴祝武,项树林.极大极小投资组合选择和均衡价格系统[J].系统科学与数学,2009,29(6).