基于随机场理论的吹填土土性参数空间变异性

张明，赵有明

（1.河南工程学院土木工程系，河南郑州 451191；2.中国铁道科学研究院，北京 100081）

0 引言

岩土参数具有明显的离散性，土性指标与所处的空间位置有关，具有空间自相关性。土性空间自相关性概念由Cornell[1]提出，大量数据显示，这种自相关性的确存在，主要表现为土层中任意两点的土体特性存在自相关性，随着两点距离的增加，这种相关性减小[2]。岩土参数的获取通常是对一定范围内地基土试验参数进行点统计，所求得的特征值不能代表一定范围内参数的空间平均特性，即“点特性”。采用点特性选取岩土参数，不利于进行岩土工程可靠性设计。换言之，由于缺乏考虑岩土参数的空间变异性，勘察数量布置的有效性值得深思。传统勘察方案在钻孔间距、最少测试或采样数量等方面都没有考虑这些问题。因此，如何有效地评价工程场地岩土参数的空间变异性，将有利于进行岩土工程可靠性设计。Vanmarcke[3]1977年提出的土层剖面随机场模型，将岩土参数的空间分布视为一随机场，用方差折减系数把土性点变异性与空间变异性联系起来，使土性“点特性”转化成“空间特性”，能较好地描述土体的空间变异性。

本文利用随机场理论，通过采用以空间递推法平均法为基础的曲线极限法求取相关距离的方法，对某围海造陆工程中吹填淤泥与原状淤泥组成的双层软土土性参数的点变异特性与空间变异特性进行研究，研究结果对于岩土工程勘察具有重要的实践意义，对吹填土土性参数的空间变异性评价与岩土工程可靠性设计具有重要的指导意义。

1 随机场理论

根据随机场理论，将土性参数沿深度变化模拟为一维随机场，土性参数的空间平均特性可通过一随机积分表达为：

式中：h为土层厚度；Z为计算土层的深度变量。随机场的数学特征值[4]：

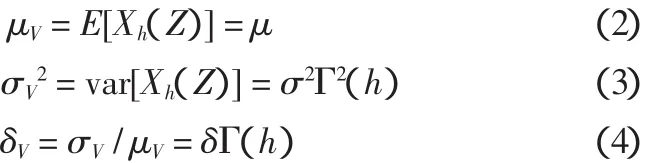
式中：μ，σ2，δ分别为土性参数点均值，点方差，点变异系数；μV，，δV分别为土性参数空间均值，空间方差，空间变异系数；Γ2（h），Γ（h）为方差折减系数，标准差折减系数。h充分大时，有近似公式：

式中：λ为相关距离。方差折减系数的近似公式可表示为：

式中：h为取样间距ΔZ0的整数倍，即：h=iΔZ0（i=1，2，…，n），代入式（3）、（5）分别得：

由式（4）～式（6）可见，随机场理论正是通过基于相关距离得到的方差折减系数，把土性参数的点变异性和空间变异性联系起来。

2 土层的相关距离

土性参数由点特性到空间平均特性的过渡，关键在于计算土性参数的相关距离。相关距离λ可以看成是衡量两个相隔一定距离的物理量之间的相关程度的基本距离，两点之间距离小于λ时认为是强烈相关的，反之则认为基本不相关。相关距离的计算方法，常用的有递推空间法、相关函数法、半变异函数法、平均零跨距法、统计模型法及基于递推空间法的一些改进方法，如曲线极限法、空间递推平均法、最大值法、试算拟合法等。许多学者对递推空间法与相关函数法进行了改进，以提高其适用性与准确性：一些学者[5]认为这两种方法求解结果十分接近；闫澍旺等[6]也从理论上证明样本容量足够大时这两种方法的计算结果一致。李小勇[7]等对各种计算方法进行了对比研究，认为曲线极限法计算结果受所选拟合函数类型的影响较大，递推空间法只要按照取样间距与相关距离接近的原则进行迭代，计算结果比较稳定。本文采用以空间递推平均法为基础的曲线极限法计算相关距离，此法具有概念明确、计算简便等优点，计算步骤如下：

1）选取取样间距ΔZ0，以连续取样的土性指标作为样本值，计算样本点均值μ和点方差；

2）把顺序相邻的i（i=2，3，…，n）个样本的均值作为一个新的样本空间，求其均值及方差，此方差为空间方差，由式（7）计算方差折减系数

3）将数据组[h，Γ2（h）]变换为数据组[h，hΓ2（h）]，令：x=h，y=hΓ2（h），采用合适的函数y=f（x）进行拟合，拟合函数满足下列条件：①y→∞时，y=f（x）的极限存在；②y＞λ时，Γ2（h）＜1；③具有一定的拟合精度。例如函数：

或

是可行的，则：

式（9）中，令X=x2，Y=x2/y，可变换为：Y=a+bX。令X=x，Y=x/y，式（10）也可变换为：Y=a+bX，按照最小二乘法可求得参数a和b，即求出了相关距离λ。

3 实例分析

某填海造陆工程，原始地貌为滨海滩涂区，规划为现代物流产业滨海区，总规划面积242.22万m2。该项目按使用功能划分为9个区，其中A、B1、B2、C2、C3、C4六个区，采用码头疏浚港池淤泥及修船基地表层淤泥机械吹填形成，在6～12m厚的原状淤泥之上形成厚度为4～6m的吹填淤泥，吹填后塘内淤泥呈泥浆状态。经过一段时间的晾晒后，依据分区不同布置钻孔取样进行室内试验和十字板剪切试验。试验项目主要包括：天然含水量w0，孔隙比e0，天然密度ρd，液、塑限IL、IP，十字板剪切强度Cu，灵敏度St等。十字板剪切试验在吹填淤泥与原状淤泥层中每隔1m试验1次，分别测试原状土、重塑土的抗剪强度。

在整个场区内选取十字板剪切试验孔共22个，以十字板剪切强度指标建立一维随机模型，取样间距ΔZ0=1m，吹填淤泥和原状淤泥的相关距离计算结果如表1所示。由表可见，吹填淤泥层的相关距离比原状淤泥小，相关距离的变异系数比原状淤泥大，表现出更大的变异性。在95%的置信率条件下，吹填淤泥与原状淤泥相关距离的区间估计分别为0.45～0.53m与0.65～0.71m，此区间可作为钻孔取样最小竖向间距选取的参考值。

表1 土层相关距离

吹填场地各区土性参数的点变异系数如表2所示。由表可见，同一场区，吹填淤泥同一土性参数的点变异系数比原状淤泥大，评价土的结构性与扰动程度的灵敏度指标St的点变异系数最大，表现出最大的变异性。由于吹填形成时间与形成过程等不同，各场区吹填淤泥土性参数表现出不同的变异性。含水量、孔隙比、液限指数、十字板剪切强度的点变异系数分别为：0.086～0.131、0.086～0.141、0.101～0.147，0.134～0.215，表现出较大的变异性。

表2 土性参数的点变异系数

吹填场地各区土性参数的空间变异系数如表3所示。由表可见：1）尽管各场区吹填淤泥与原状淤泥层厚度分布不同，但方差折减系数计算结果十分接近，在0.25～0.34之间。同一场区，吹填淤泥的方差折减系数比原状淤泥大，说明采用空间特性代替点特性选取土工参数进行可靠性设计时，空间变异性对吹填淤泥土工参数指标准确选取的影响比原状淤泥大。2）同一场区，吹填淤泥同一土性参数的空间变异系数比原状淤泥大，表现出更强的空间变异性，且灵敏度指标St的点变异系数最大，表现出最大的变异性。由表2、3比较可知，基于随机场理论计算出的各淤泥层土工参数的空间变异系数，在数值上要比点变异系数小得多。

4 结论

本文基于随机场理论，采用空间递推平均法为基础的曲线极限法计算相关距离，考虑土层相关距离与土层厚度不均对土性参数空间变异性的影响，把土性参数的点特性通过方差（标准差）折减系数转化为空间特性，应用于对某围海造陆工程吹填淤泥与原状淤泥土性参数的点变异、空间变异特性进行研究，对指导岩土工程勘察工作具有一定的指导意义，期望能更好地推动岩土工程可靠性设计与研究。得出如下结论：

1）吹填淤泥与原状淤泥相关距离的区间估计分别为0.45～0.53m、0.65～0.71m，可作为勘察工作中钻孔取样竖向间距选取的参数值。

2）吹填淤泥土性参数的点变异性与空间变异性均比原状淤泥大，由于吹填淤泥特殊的形成过程，评价土体结构性与扰动程度的灵敏度指标St的点变异系数与空间变异系数最大，表现出最大的变异性。

3）通过随机场理论计算出的土性参数的空间变异系数，在理论上更合理，在数值上比点变异系数小得多。

4）采用空间特性代替点特性进行土工参数可靠性设计时，相比于原状淤泥，空间变异性对吹填淤泥土性参数准确选取的影响更为显著，在工程应用中，更应考虑吹填淤泥土性参数的空间特性。

[1] Bjerrum L.Problem of Soil Mechanics and Construction on Soft Clays and Structurally Unstable Soils（collapsible，expansive and others）[C]//Proceedings 8th International Conference on Soil Mechanics and Foundation Engineering，MOSCOW，1973，3：111-159.

[2] 傅旭东.土工参数相关范围及相关距离的计算方法 [J].西南交通大学学报，1996，31（5）：510-515.

[3] Vanmarcke Erik H.Probabilitistic Modeling of Soil Profiles[J].Journal of Geotechnical Engineering Division，ASCE，1977，103（GT11）：1 227-1 246.

[4] 吴长富，朱向荣，刘雪梅.杭州地区典型土层抗剪强度指标的变异性研究[J].岩土工程学报，2005，27（1）：94-99.

[5] 李镜培，舒翔，丁土君.土性指标的自相关特征参数及其原则[J].同济大学学报，2003，31（3）：287-290.

[6] 闫澍旺，朱红霞，刘润，等.关于土层相关距离计算方法研究[J].岩土力学，2007，28（8）：1 581-1 586.

[7] 李小勇.土工参数空间概率特性及软黏土地基固结概率分析[D].杭州：浙江大学博士学位论文，2001.