单摆实验仪的改进＊

黄晓锋 梅掌荣

（湖州师范学院，浙江 湖州 313000）

1 引言

重力加速度是一个重要的地球物理常数.从文献［1］～［3］中可知，测量重力加速度的方法有很多种，例如电磁计时器测定法、多球下落法、单摆测量法等.在诸多方法中用单摆法测重力加速度是最简单的一种，并且容易测得较精确的g值.在文献［4］中有学者针对测量中存在的系统误差，对计算公式进行了修正，在文献［5］、［6］中提到有学者对测量方法进行了改进，例如采用计时器对周期进行测定.但在这些改进方案中，都是采用一根摆线进行摆动，所以小球在摆动时依然很容易产生圆锥摆现象.在文献［7］中，有学者曾注意到了小球的圆锥摆问题，发现这会使测量得到的周期T 偏大，但遗憾的是他只是将小球在圆锥摆情况下测得的数据进行了剔除，而不是想办法去克服小球的圆锥摆.对此，本文提出新的改进方案，采用双线摆取代单线摆，克服圆锥摆现象，同时利用光电门对小球的摆动进行计时和计数，减少人为误差的引入，提高实验的准确性和成功率，并且使实验操作更为简单和便捷.

2 实验内容

2.1 改进实验的测量方法

在改进实验中，采用双线摆取代原先的单线摆，即在单摆小球上连接两根细线，然后再次进行摆动，克服传统实验中单摆小球在摆动时出现的圆锥摆现象.在单摆小球的最低点处安装一个光电门，然后与计时器相连接，只要在实验开始前，在计时计数器中输入周期的次数，当小球开始摆动后，仪器便会自动计时.当50个周期结束之后，仪器中就会马上显示小球经历50个周期所用的时间，除以次数50，就可以得到一个稳定的周期值T.这样可以很好地避免由于人工计数所带来的较大误差，而且测量数据十分的稳定，波动性很小.

2.2 摆长的测定

根据相关公式，分析改进实验装置示意图（图1）可知：

竖直方向：

F合＝2×Fcosθ

水平方向

F合＝0

两条细线拉力的合力方向竖直向上（与CD 重合），受力情况与单摆小球时一致；振动形式也与单摆小球一致，为简谐振动；所以振动时，有效摆长为CD 段.

综上可得，摆长L＝CD＋r.

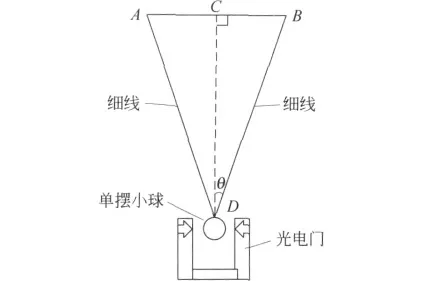
图1 改进实验装置示意图

3 实验数据及图表

从图2中可以明显观察到，传统实验中测得的重力加速度值存在着很大的波动性，测量值也不够准确，改进后测得的重力加速度值稳定性明显减小，测量值也更为准确.

表1 摆长L＝1.0003m 时测得的重力加速度值

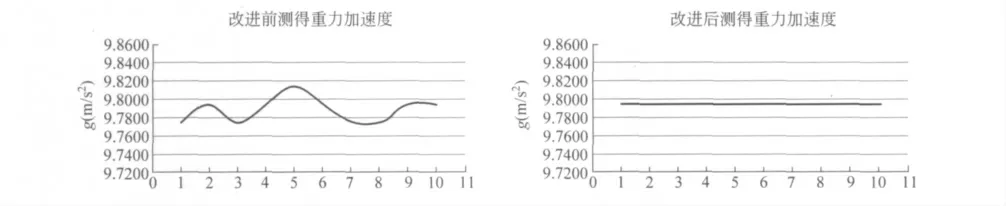
图2 改进前后测得重力加速度值对比图

根据相同的实验原理，经过改变不同的摆长，进行多次实验后归纳得到结果如表2所示.

表2 改进前后测得重力加速度值对比

从表2中可以看出，改进前的传统实验，由于存在较大的误差干扰因素，例如小球在单摆过程中产生的圆锥摆现象，并且从表2的测量数据中可以观察到，随着摆长的增加，圆锥摆的情况会越明显，从而使周期的测量值偏大，严重影响到重力加速度的准确性.

当我们采用双线摆之后，克服了传统实验中小球圆锥摆的问题，并且在计时计数器的配合下，使周期的测量更加的准确，从而得到了更加精确的重力加速度值.已知湖州地区的g＝9.794m/s2，实验改进前后的两组数据与其进行比较之后，发现改进后实验测量结果的准确度显著提升.

4 结论

在改进的实验中，测量得到的重力加速度g值更加的稳定，而且不受摆线长短的影响，测量值更为准确，同时提高了实验的成功率，改进后实验的操作也更加的简单和便捷.这对实验的改进具有实质性的意义.

［1］朱端兴，曹正东.落球法测定重力加速度实验的改进［J］.大学物理实验.2002，15（3）：25～29

［2］孟宪斌.对重力加速度量值的认识［J］.电大理工科学及工程研究，2009，（2）：56～57

［3］郝建明，李咏波，和伟.单摆法测重力加速度的修正公式分析［J］.云南师范大学学报，2004，24（3）：63～66

［4］袁庆新，李亮.任意振幅单摆周期近似公式［J］.物理与工程，2009，19（5）：11～12

［5］魏薇.单摆振动实验数字化演示的定量分析［J］.物理与工程，2011，21（5）：6～9

［6］赵平华.用单摆测重力加速度实验的改进［J］.物理通报，2002，（4）：34～35

［7］张克.“用单摆测重力加速度实验”的改进［J］.安徽教育，2003，（20）：33～34