分子间的吸引相互作用在处理实际气体行为中的影响

张永梅

（中北大学理学院物理系，山西 太原 030051）

实际气体只有在高温低压下近似地符合理想气体状态方程，而在高压低温下，一切气体均出现明显的偏差.如图1为实验测得H2在不同温度下pV－p 曲线［1］.可见实际气体对理想气体的偏差随温度的降低而增大.实际气体之所以对理想气体产生偏差，是由于实际气体不符合理想气体的微观模型，即实际气体的分子间存在相互引力且分子本身有一定的大小.本文在考虑分子大小的前提下，讨论了不同形式的分子引力在描述实际气体行为中的影响.

1 pV－p等温线

考虑到气体分子本身的大小，理想气体状态方程可修正为p（V－b）＝RT，展开可得pV＝RT＋pb.可见仅考虑分子的体积作用时，pV－p 等温线是一条直线，与实际气体的行为偏差很大.下面我们通过在状态方程中引入不同形式的引力项，分析分子间引力对pV－p 等温线的影响.

1.1 范德瓦尔斯气体的pV－p等温线

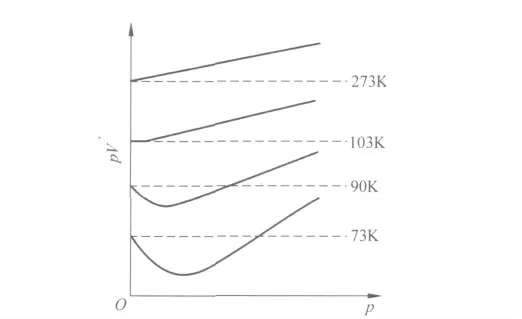
图1 H2 在不同温度时的pV－p 关系

1873年荷兰科学家范德瓦尔斯根据气体的具体情况，对理想气体状态方程作了修正.1 摩尔范德瓦耳斯气体的状态方程为

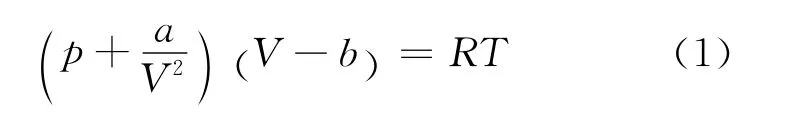
将式（1）展开，可得

这一方程揭示了实际气体与理想气体的微观差别，它的缺点是方程中吸引项无有关温度的影响.

1.2 伯塞洛特气体的pV－p等温线

考虑到分子间吸引相互作用与温度有关，伯塞洛特方程在引力项a 中引入了温度因子.1 摩尔伯塞洛特气体的状态方程［2］为

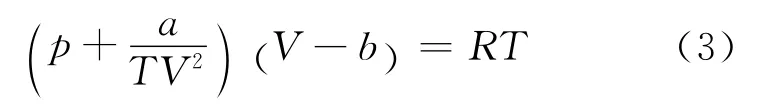
将式（3）展开，可得

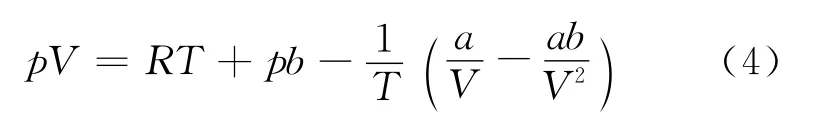
根据式（2）、（4）可得，实际气体的分子引力和分子体积效应对pV 是两个相反的影响因素.高温时，分子间的相互吸引可以忽略，即含a 的项可以略去，从而得到pV＝RT＋pb，即pV＞RT，且随压力的升高而增大.在低温低压范围，分子的引力起主要作用，即含b 的项可以略去，可得pV＜RT，其数值随p 的增加而减小.当压力增大到一定程度，矛盾双方发生转化，分子的体积效应变成矛盾的主要方面，于是随压力升高pV 值增大.因此在低温时，是pV 值先随p 的增加而降低，经过最低点又逐渐上升.比较式（2）、（4）可得，吸引项中温度因子的引入只是使得吸引项的影响减小.

2 Boyle温度

pV－p 等温线中，曲线的最低点移至纵轴上时对应 的 温 度 定 义 为Boyle温 度TB［1］，可 由 下 式求得

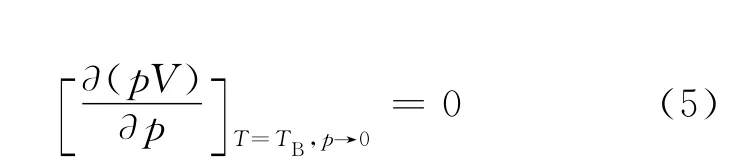
当不考虑引力项时，根据上式可得

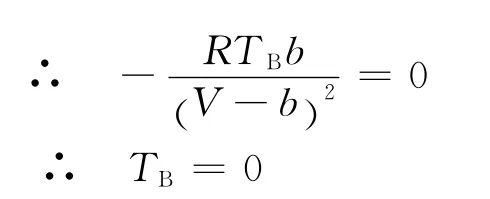
2.1 范德瓦尔斯气体的Boyle温度

将式（1）改写为

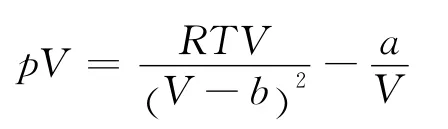
根据式（5）同理可得

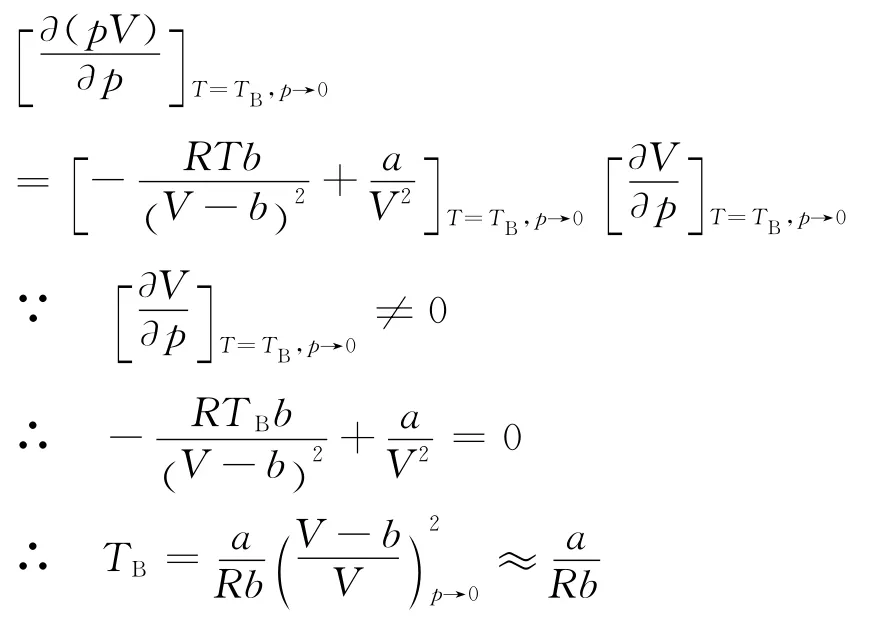
代入a和b 的值可得

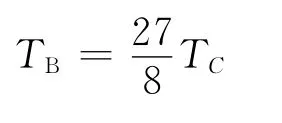
2.2 伯塞洛特气体的Boyle温度

将式（3）改写为

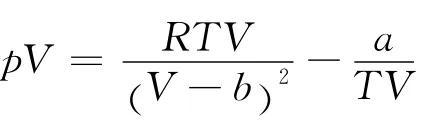
根据式（5）同理可得

代入a和b 的值可得

3 结论

通过上面的分析可得出以下结论：

（1）分子间的引力在描述实际气体行为中具有重要的意义.虽然伯塞洛特气体状态方程与范德瓦尔斯气体状态方程的展开形式不同，但在对实际气体的pV－p 等温线的解释上，两种气体的结论却完全一致.吸引项中温度因子的引入只是使得吸引项的影响减小.

（2）当不考虑引力项时，Boyle温度为零；考虑了引力项后，Boyle温度与气体的临界温度有关，不同气体的Boyle温度不同，这更符合实际气体的行为.吸引项中的温度因子只是使Boyle温度的数值减小，并没有改变其本质.

［1］朱文涛.物理化学［M］.北京：清华大学出版社，1995.9

［2］谢锐生.热力学原理［M］.北京：清华大学出版社，1980.77