考虑几何非线性的长输管线地震响应分析*
杨竟南 余 涛 雷 凡
(武汉理工大学交通学院1) 武汉 430063) (湖北省鄂州市公路管理局2) 鄂州 436000)
0 引 言
随着我国工业的快速发展,管道运输系统已经越来越多地应用于各种领域,如城市供水长距离管线、大规模集中供暖系统、长距离油气管线等,这些管道系统对国民经济以及人民生活都起着十分重要的作用,因而被称为“生命线工程”[1].与地上建筑物相比,地下管道通常分布的范围广,不可避免地涉及各种场地,在地震中极易遭受破坏,造成系统故障和中断,并有可能产生各种次生灾害[2],给人民的生活、生命和财产安全带来严重危害.因此,对管道系统的震害分析十分重要.
目前,地震响应动力分析方法主要有3种:反应谱法、时程分析法和随机振动方法[3].本文采用时程分析法对地震作用下的长输管线的动力响应进行分析,并探讨了管线悬跨段长度、地震强度、几何非线性等因素对其地震响应的影响.
1 地震响应分析方法
地震作用下,多自由度体系的振动方程为[4]

式中:M,C,K分别为多自由度体系的质量矩阵、阻尼矩阵和刚度矩阵;U,˙U,¨U 分别为结构 的 动 力位移、速度和加速度列阵;I为地面运动影响系数列阵(t)为地面运动加速度.
直接积分时程法是对结构物的运动微分方程直接进行逐步积分求解的一种动力分析方法[5].在利用数值方法逐步积分时,将式(1)化为增量运动微分方程组

假定在时间间隔内位移、速度和加速度按一定规律变化(如Newmark法),求解式(2)可得到各质点随时间变化的位移、速度和加速度动力反应,进而可计算出构件内力的时程变化关系.
2 计算模型
为分析长输管线在地震荷载作用下的动力响应,选取长度分别为20,30,40m的管线进行分析,假设管线两端为固定支承.计算中管线采用三维实体单元按管线实际尺寸进行离散.计算模型见图1.40m长的管线纵向划分为160段,划分网格后单元总数为7 680,节点总数为11 592.
管线尺寸及材料参数按表1选取.
图1 管线计算模型图

表1 模型基本参数
3 地震波的选取
目前,在抗震设计中有关地震动加速度时程的选择主要有3种方法[6]:直接利用强震记录、采用人工地震加速度时程和采用规范标准化地震加速度时程.
本文采用直接采用强震记录的方法来进行地震响应分析,所采用的地震波为El Centro波.地震动持时为30s,时间间隔为0.02s,并沿坐标x方向输入,经调整,计算中取加速度峰值分别为0.5,1,2,4m/s2的地震波进行计算.地震加速度峰值取4m/s2时,地震的加速度时程曲线见图2.

图2 El Centro波加速度时程
4 地震反应分析
对3种管线施加不同的强度地震荷载,分别对考虑管线大变形和不考虑管线大变形2种情况进行计算,得到管线的变形图和应力分布图(见图3),管线的动力响应时程曲线,取各管线跨中节点的位移响应和应力响应,如图4所示(在此仅列出地震加速度峰值为4m/s2时的响应).
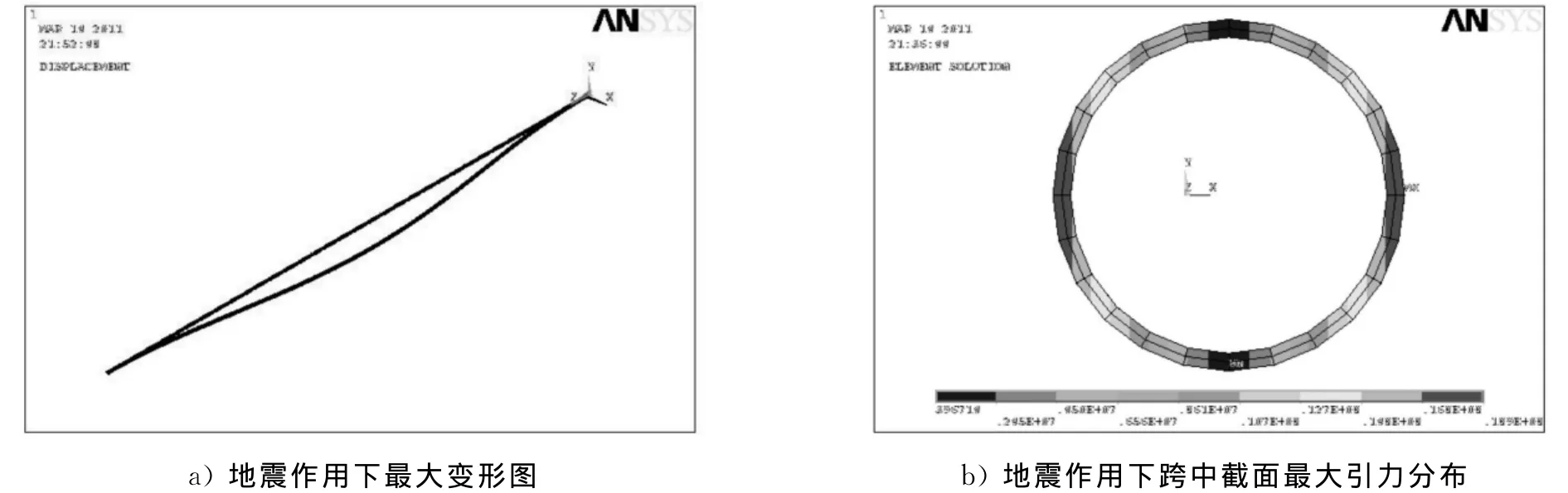
图3 40m长管线变形图和应力分布图

图4 地震加速度峰值为4m/s2 时的响应
从图4可以看出,位移响应和应力响应随时间的变化趋势基本一致.比较不同长度管线的地震响应可以看出,较长管线的振动周期也较长,这与其固有频率的关系是对应的.观察考虑和不考虑管线大变形的地震响应曲线,当地震加速度峰值为0.5m/s2时,各管线考虑大变形和不考虑大变形的地震响应均比较接近,当地震加速度峰值为4m/s2时,20m长管线考虑大变形和不考虑大变形的地震响应也比较接近,而30m和40m长管线的地震响应存在较大差异,这些差异是由于较长管线在强烈地震动作用下产生了较大的变形,由变形产生的应力对管线产生的影响所致.
为进一步分析大变形效应对管线动力响应的影响,图5分别就考虑大变形和不考虑大变形两种情况,给出了地震作用下各管线跨中位移响应峰值和应力响应峰值随管长的变化曲线.

图5 地震响应峰值随管长的变化曲线
比较图5中位移响应峰值可以看出,当管长为20m时,考虑大变形和不考虑大变形的最大位移基本一致;当管长为30m时,考虑大变形和不考虑大变形的最大位移也十分接近,仅当地震加速度峰值为4m/s2时,考虑大变形的最大位移较大;当管长为40m时,考虑大变形时的最大位移较大.应力响应峰值曲线显示,不论跨长如何,当考虑管线大变形时,其跨中节点的应力响应较大.且管线长度越长、地震强度越大,考虑大变形和不考虑大变形的位移及应力响应计算结果差异越大.因此在对较长线进行地震响应分析时,考虑大变形的影响是十分必要的.
为分析地震强度对管线动力响应的影响,图6列出了考虑大变形和不考虑大变形2种情况下,地震加速度峰值分别为0.5,1,2,4m/s2时,各管线的跨中节点位移响应峰值和应力响应峰值随地震强度的变化曲线.
由图6可以看出,随着地震加速度峰值的增大,管线跨中节点的最大位移响应和应力响应也相应增大,当不考虑管线大变形效应时,图中曲线接近线性增长,而考虑管线大变形效应时,图中曲线为折线增长.对于20,30,40m长的管线,当地震加速度峰值小于1m/s2时,考虑和不考虑管线大变形效应的地震响应基本一致;当地震加速度峰值为2m/s2时,20m和30m长管线的地震响应在考虑和不考虑大变形情况下的结果也比较接近,考虑大变形情况下,40m长管线的地震响应偏大;当地震加速度峰值为4m/s2时,3种长度的管线在考虑和不考虑大变形情况下的地震响应均存在较大差异.因此在地震强度较大时,对较长管线应考虑大变形的影响.

图6 地震响应峰值随地震强度的变化曲线
5 结 论
地震作用下,管线的位移和应力响应曲线随时间的变化趋势基本一致;较长管线的地震响应振动周期也较长;当地震强度较大,管线较长时,考虑大变形和不考虑大变形的管线地震响应存在较大差异,应考虑大变形因素的影响.
[1]郝婷玥,陈贵清,马卫华.地震作用下埋地管道横向振动分析[J].四川建筑科学研究,2010,36(2):204-207.
[2]梁 瑞,颜鹏飞,邵松伟,等.埋地管道在地震波作用下的动力响应分析[J].兰州理工大学学报,2008,34(6):148-150.
[3]范立础,胡世德,叶爱君.大跨度桥梁抗震设计[M].北京:人民交通出版社,2001.
[4]董汝博.多点地震动作用下海底悬跨管道非线性分析[D].大连:大连理工大学,2008.
[5]党慧慧.潜浮式倒悬索跨海大桥地震反应研究[D].武汉:武汉理工大学,2009.
[6]李爱群,丁幼亮.工程结构抗震分析[M].北京:高等教育出版社,2010.

