城市公交系统规划方案的综合评价*
(新疆农业大学机械交通学院 乌鲁木齐 830052)
城市公交系统规划方案比选是一个多指标决策过程,评价指标间可能存在模糊不相容问题,而物元分析理论以促进事物转化、解决不相容问题为核心,适用于多因子评价问题.本文利用物元分析原理,结合模糊集和欧氏贴近度概念,将信息论中的熵值理论引入权重计算中,在此基础上建立基于熵权的城市公交系统规划方案模糊物元评价模型,对城市公交系统进行实证研究,以有效避免评价标准不确定性带来的影响,尽量全面、客观地进行城市公交系统规划方案评价.
1 评价指标体系构建
1.1 公交系统规划影响因素分析
1)技术角度 主要包括网络规模与结构特征合理性;出行特征是否满足需求预测结果;公交出行特征是否达到相关服务水平要求;道路运行特征是否体现高效.
2)国民经济与社会效益 主要包括是否支持城市发展;社会可接受度;安全与环境的影响.
3)可实施性 主要包括财政可行性;实施的难易程度.
1.2 评价指标体系建立
公交系统规划的影响因素可归纳为技术角度、国民经济与社会效益、方案可实施性3个层面,每一层下又可分为更多因素,且各影响因素的评价标准不同.结合各指标的特点以及在规划方案评价过程中的实用性,在借鉴相关研究成果的基础[1-2]上,采用理论分析、经验选取和专家咨询相结合的方法,最终确定公交系统规划方案评价指标体系见表1.
2 模糊物元评价模型
2.1 模糊物元及复合模糊物元
在物元分析中所描述的事物M及其特征C和量值x组成物元R=(M,C,x)或R=(M,C,C(M)),同时把事物的名称、特征和量值称为物元3要素[3-4].如果物元模型中的量值x 具有模糊性,便称其为模糊物元.事物M 有m 个特征C1,C2,…,Cm及其相应的量值x1,x2,…,xm,则称R为m维模糊物元.n个事物的m维物元组合在一起便构成n个事物的m维复合模糊物元Rnm:

表1 公交系统规划方案评价指标体系

式中:Rnm为n个事物的m 个模糊特征的复合物元;Mi为第i个事物(i=1,2,…,n);Cj为第j个特征(j=1,2,…,m);xji为第j个事物第i个特征对应的模糊量值.
2.2 从优隶属度模糊物元
由于各评价指标特征值对于方案评价来说,有的是越大越优,有的是越小越优,因此,对于不同的隶属度分别采用不同的计算公式,计算隶属度的公式有很多,为了更充分地反映安全评价各指标的相对性,采用如下形式:

式中:μji为从优隶属度;max xji,min xji分别为各方案中第i个 (i=1,2,…,m)评价指标中的最大值和最小值.由此构建从优隶属度模糊物元

2.3 标准模糊物元与差平方复合模糊物元
标准模糊物元R0m是指从优隶属度模糊物元~Rnm中各评价指标的从优隶属度的最大值和最小值.本文以最大值作为最优,也就是各指标从优隶属度均为1.
若以Δji(i=1,2,…,m;j=1,2,…,n)表示标准模糊物元R0m与复合从优隶属度模糊物元~Rnm中各项差的平方,则组成差平方复合模糊物元RΔ,即Δji=(μ0i-μji)2,RΔ可表示为
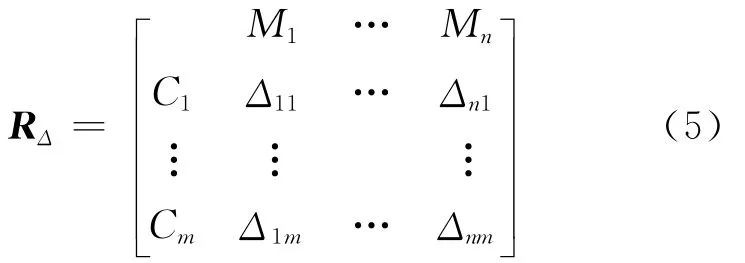
2.4 熵值法确定权重系数
在信息论中,熵值反映了信息无序化程度,其值越小[5],系统无序度越小,故可用信息熵评价所获系统信息的有序度及其效用,即由评价指标值构成的判断矩阵来确定指标权重,它能尽量消除各指标权重计算的人为干扰,使评价结果更符合实际,其计算步骤如下.
步骤1 构建m个事物n个评价指标的判断矩阵R=(xji)n×m,(i=1,2,…,m;j=1,2,…,n).
步骤2 将判断矩阵归一化处理,得到归一化判断矩阵B.
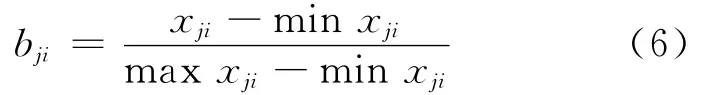
式中:max xji,min xji分别为同指标体系j下不同事物中最满意者或最不满意者(越小越满意或越大越满意).
步骤3 根据熵的定义,n个评价事物m 个评价指标,可以确定评价指标的熵为
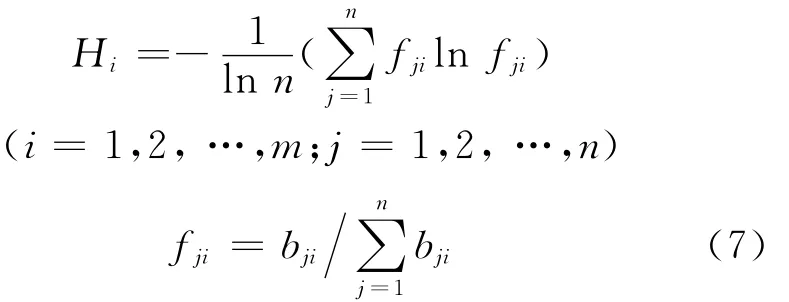
为使ln fji有意义,当fji=0时,根据评价的实际意义,可以理解ln fji为一较大的数值,与fji相乘趋于0,故可认为fjiln fji=0.但当fji=1,fjiln fji也等于0,这显然与熵所反映的信息无序化程度相悖,不切合实际,故需对fji加以修正,将其定义为

3.3 贴近度和综合评价[6]
贴近度是指被评价样品与标准样品两者互相接近的程度,其值越大表示两者越接近,反之则相离较远.从而,可以根据贴近度的大小对各方案进行优劣排序,也可以根据标准值的贴近度进行类别划分.考虑到本文的具体评价意义,采用欧氏贴近度ρHj作为评价标准,运用(·,+)算法(即先乘后加)来计算和构建贴近度复合模糊物元

3 实例分析
乌鲁木齐市位于中国的西北部,是新疆维吾尔自治区的首府,是新疆政治、经济、文化的中心,主要由天山区、沙依巴克区、新市区、水磨沟区、头屯河区、米东新区以及达坂城区等7区及乌鲁木齐县1县共同构成.截至2010年,乌市拥有总人口数约311万,面积约为235.9km2,城市主体发展格局主要呈现出南控北扩的特征.
近些年,随着乌市社会经济的快速发展,机动车拥有量增长速度尤为明显.2001年乌市拥有机动车仅为8.1万辆,其后平均每年以16.7% 的增幅增长,截至2010年6月乌市机动车的已超过30万辆.机动车迅速发展的势头,导致了城区通堵塞的现象更为普遍.
为此,乌鲁木齐市加强了改善城市交通状况的有效措施的研究,规划了未来公交系统改善方案[7],见表2.本文采用模糊物元法对公交系统改善方案进行排序.
根据表2的基本数据建立公交系统规划方案的复合模糊物元Rnm:

?
用熵权法确定各指标权重为

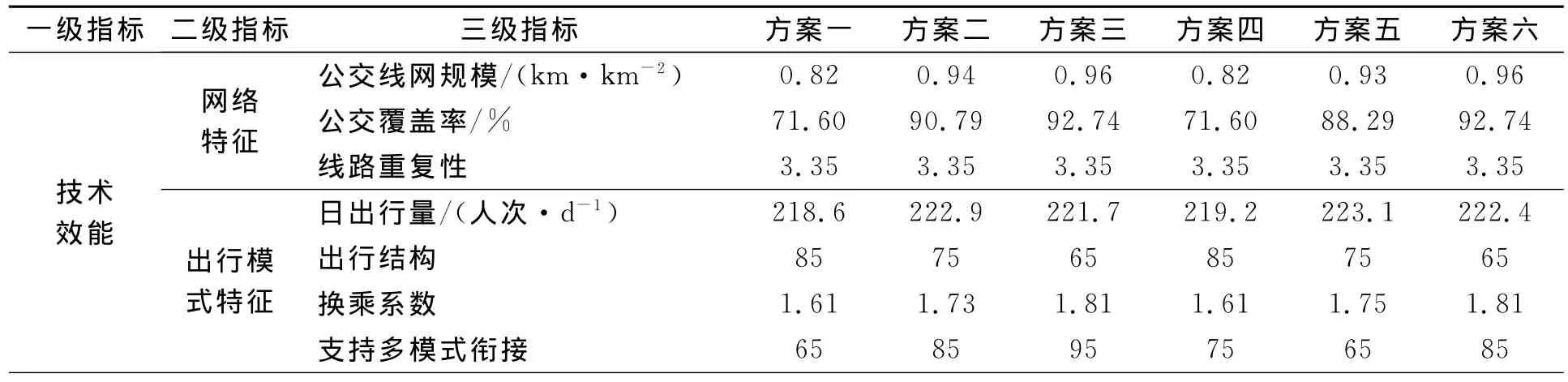
表2 公交系统规划方案评价指标值
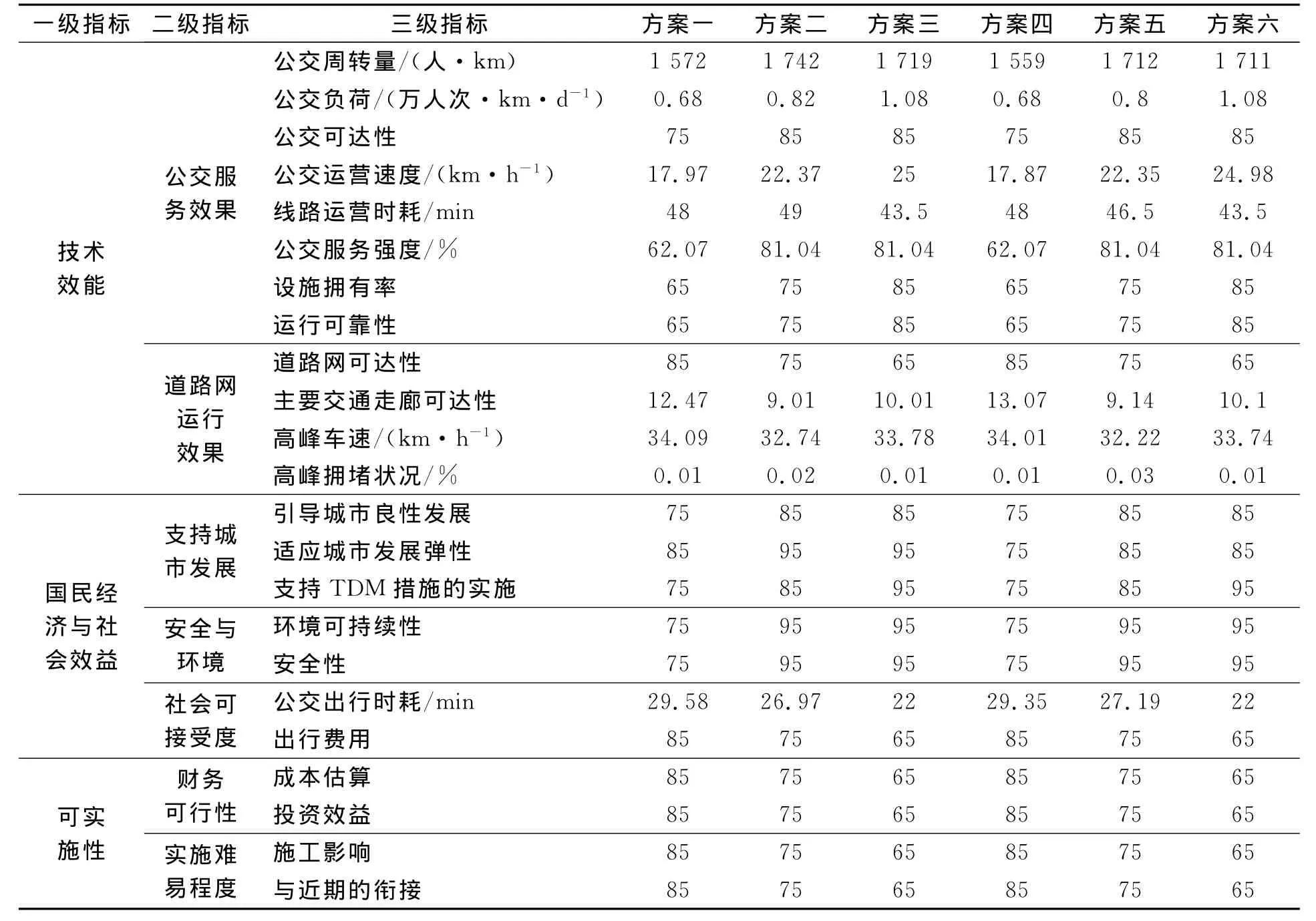
续表2

?
根据标准模糊物元和~Rnm构建差的平方模糊复合物元RΔ:

?
由式(10)可以得到各方案的贴近度RρH

根据计算得出的贴近度从大到小排序,该市公交系统规划方案优选依次为方案二>方案六>方案五>方案三>方案四>方案一.上述计算结果与文献[7]结果一致.
4 结束语
将模糊物元理论应用于乌鲁木齐市公交系统规划方案的综合评价中,建立了基于熵权的模糊物元综合评价模型,得出各方案的比选结果.该评价方法丰富和改进了公交系统规划方案,且计算简单、方便,结果合理.引入熵值理论,从数据本身所反映的信息无序化效用值来计算权重系数,可以有效地减少其计算的主观性.另外,此方法还可应用于城市交通项目决策、招投标综合评价等方面,具有广泛的推广前景.
[1]胡启洲.城市常规公共交通系统评价方法研究[D].南京:东南大学,2008.
[2]胡启洲,陆化普,蔚欣欣,等.基于关联嫡与复合物元的公交系统综合测度模型[J].系统工程理论与实践,2011,31(1):186-192.
[3]蔡 文.物元模型及其应用[M].北京:科学技术文献出版社,1994.
[4]张 斌,雍歧东,肖芳淳.模糊物元分析[M].北京:石油工业出版社,1997.
[5]闫文周,顾连胜.熵权决策法在工程评标中的应用[J].西安建筑科技大学学报,2004,36(1):98-100.
[6]肖芳淳.输气管道土壤腐蚀性模糊物元贴近度聚类分析[J].油气储运,1999,18(6):35-37.
[7]阿特金斯顾问(深圳)有限公司.乌鲁木齐市公共交通规划研究[R].上海:阿特金顾问(深圳)有限公司上海分公司,2010.

