高校教师教学质量评估体系研究——基于AHP的模糊综合评价方法应用

□文/尹亮亮 苏兴 武萌

（河北金融学院河北·保定）

高校开展教学质量评估是加强师资队伍建设和管理、全面提高教学质量、深化教育改革的有效措施，是学校实施规范化、科学化管理的重要手段。现今，各高校结合本院校特色以及教育教学发展规划，制定了针对教师教学质量的评估措施以及手段，并将其作为教师评定职称、年终考核的重要考评措施。

由于教学质量考核涉及面广泛，影响教师教学的因素又较为复杂多样，传统的对教师教学质量评价方法一般以定性分析为主，无法摆脱主观片面性。近年来，虽然高校在评价体系定量分析方面做出了大量的尝试与突破，但由于所建立的评价指标没有设置必要的权重或者人为设置权重，导致评价体系无法全面、准确地对教师教学质量做出科学的评价。

鉴于教师教学质量高低的衡量界限是一个十分模糊的难以量化问题，对于模糊对象的评价，过分的精确反而模糊。因此，本文通过对层次分析法与模糊综合评价法的研究，综合二者在评价决策理论中的各自特点，建立基于层次分析法（AHP）的模糊综合评价模型，即用AHP建立教学质量评价指标体系的层递关系以及权重向量，再利用模糊算子的综合运算得出综合评价，从而建立兼顾科学性与实用性的教学质量综合评价体系。

一、评价体系基本方法简介

1、层次分析法（AHP），是实现思维过程、主观判断规范化、数量化的基本方法。为了对较为复杂问题做出正确的认识以及最终的决策，往往将所涉及决策的相关因素分成目标、准则、方案等多个层次。结合客观事实，利用数学方法，计算每个层次内全部因素相对重要性的权重值，以此进行综合评价、定量分析和比较，最终做出决策。对于教学质量评价来说，由于其影响因素的复杂性，可以将其划分成不同层次，以便确定不同层次的权重大小，从而得出各层次对教学质量评价的影响程度。

2、模糊综合评价法，是以模糊数学为基础，利用考察对象的基本特征、影响因素等组成模糊集合，构建适当的隶属函数，运用模糊集合论中的变换运算，对考察对象进行定量分析，并最终做出综合评价的基本方法。由于教学质量评价中所涉及的许多评价标准均带有模糊性，即不存在十分明确的肯定或者否定。而对于这些非线性的评价，也只有通过模糊运算法则，才能较全面地汇总各评价的主体意见，得到可比的量化结果。因此，对教学质量采用模糊综合评价法，会更加科学地反映评价对象的优劣程度，分析结果也将更加接近实际情况。

二、基于AHP的教学质量模糊综合评价体系构建

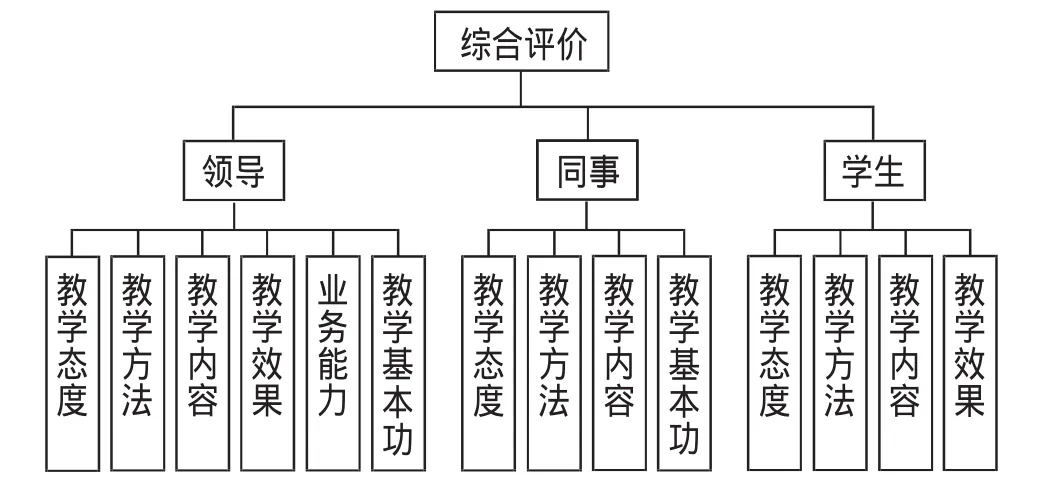
图1 教学质量评价指标结构图

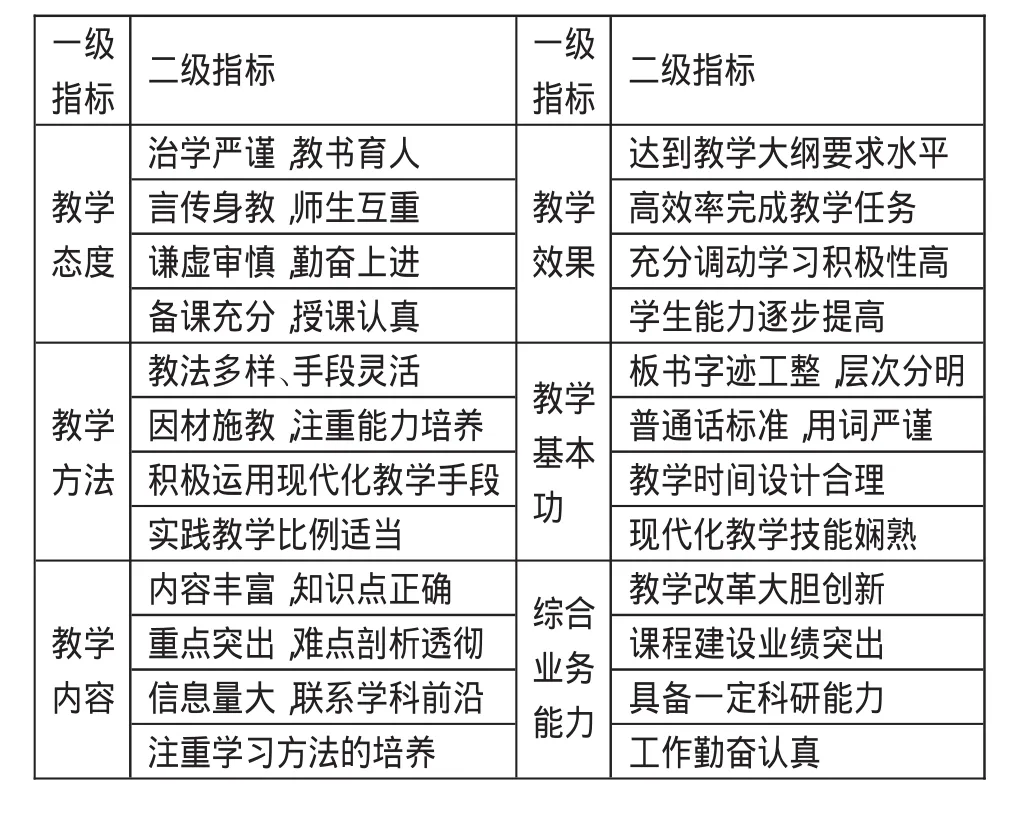
表1 评价体系基本评价内容

基于AHP的模糊综合评价体系主要分为教学质量评价体系的AHP模型和模糊综合评价多级模型两大部分。AHP模型是整个评价体系的基础框架，为后期模糊评价提供了强有力的数据支撑；模糊综合评价则是运用模糊数学的基本变换方法，对前期量化后的权重数据以及模糊集信息进行综合处理，从而得到最终的评价结果。

鉴于此，综合评价的基本步骤为：确定评价对象；建立评价指标体系；利用AHP计算各评价指标的权重系数；构造模糊综合评价多级模型；分析计算综合评价值，最终做出评价。

（一）教学质量AHP模型的构建

1、确定评价对象，建立评价指标体系。根据高校实际情况，建立科学的教学质量评价指标体系。评价指标应符合严谨的教学规律，体现教学本质，既兼顾高校自身发展的特色，又能够体现教育改革的发展方向。另外，评价指标之间既具备整体完备性，同样又具有度量的可测性。

鉴于上述原则，我们从学生、同事、领导三个角度出发，分别围绕教学态度、教学内容、教学方法、教学效果、综合业务能力等评价内容，按照不同指标做出优秀、良好、合格、不合格四个等级评价。

值得说明的是，教学态度、教学方法、教学内容是领导、同事以及学生共同评价的，具体内容基本一致。而结合实际情况，领导评价体系中增加了综合业务能力指标；同事评价中，用教学基本功替代了教学效果，使体系结构更加接近现实，相对较为合理。

评价指标层次结构如图1所示。（图1）指标体系结构中目标层位于最顶层，中间部分为准则层，方案层位于最下层。当然，根据研究问题的复杂程度，当指标设计因素较多时，无论准则层还是方案层均可近一步划分若干子层，形成多级指标体系。

结合近年来高校普遍进行的教学质量评测规则，综合能够反映教学质量的多方面因素，设立本评价体系的二级评价指标，如表1所示。当然具体的评价内容并非一成不变，领导、同事、学生三方面看待同一问题的角度也会略有不同，本文只是由于篇幅有限，故将评价内容统一简化。（表1）

2、利用AHP确定指标权重集。权重集是反映指标因素间重要程度关系的集合，具有较强的导向作用。权重集的导出依赖于客观、科学的对于指标因素进行相互比较，从而初步实现数据的量化，具体步骤如下：

（1）根据指标内容构造判断矩阵C。判断矩阵是根据本层次中每个因素的具体内容，考虑对上一层指标因素的影响作用，依照1-9标度理论进行两两比较所得到的综合数据表，其特点在于aij=1/aji，aii=1，aij＞0。例如，判断矩阵中aij=7表示ai较aj十分明显重要，aij＝3表示ai较aj略微重要。

（2）层次权重排序，导出权重集。对n阶判断矩阵C按列归一化得，其中i，j=1，2…n）；计算，，其中归一化，导出权重集W＝（w1，w2，…wn），其中

（3）判断矩阵的一致性检验。对评价因素进行比较时，任何一个判断失误都可能导致不合理排序的出现，此时的判断矩阵不具备完全一致性。引入一致性比例CR，若CR＜0.1则说明判断矩阵具有满意的一致性，否则需修改判断矩阵。

CR＝CI/RI，其中CI＝（λmax-n）/n-1，，RI为平均随机一致性指标。

（二）模糊评价多级模型。根据前面构建的评价指标层次结构可以看出，无论是学生、同事还是领导，各评价子体系均

具有二级评价指标，因此首先应该对每个一级指标所分解的下一级指标（二级指标）进行综合评判，再结合各一级指标自身的权重进行模糊变换，最终得到各子体系二级模糊评判结果。其实多级评判模型无非就是多次重复着统一的模糊评判过程，该过程具体步骤如下：

1、确定评价对象的评价因素（指标）集C＝｛c1，c2，…cn｝，即将评价目标看成由多个因素组成的模糊集合C。设定用于评价因素评审等级的评语集V＝｛v1，v2，…vm｝以及用于量化评价结果的数值集N＝｛N1，N2，…Nm｝。

2、建立模糊评价关系矩阵（隶属度矩阵）：

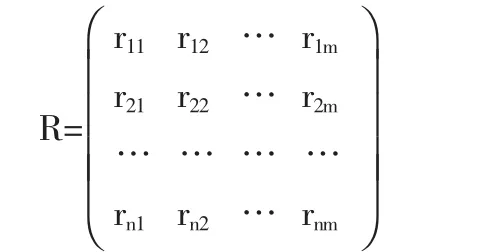
表示被评价对象从指标因素ci角度分析对评判等级vj的隶属程度。

3、结合AHP导出的指标权重集W与隶属度矩阵R进行模糊变换运算，从而得到综合评价结果矩阵S。

S＝WR

其中，si表示被评价对象整体而言对vi评判等级的隶属程度。

4、利用模糊评价矩阵与数值集导出评价最终成绩。

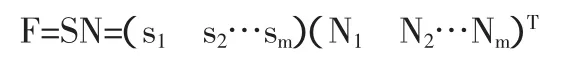
三、综合评价计算实例

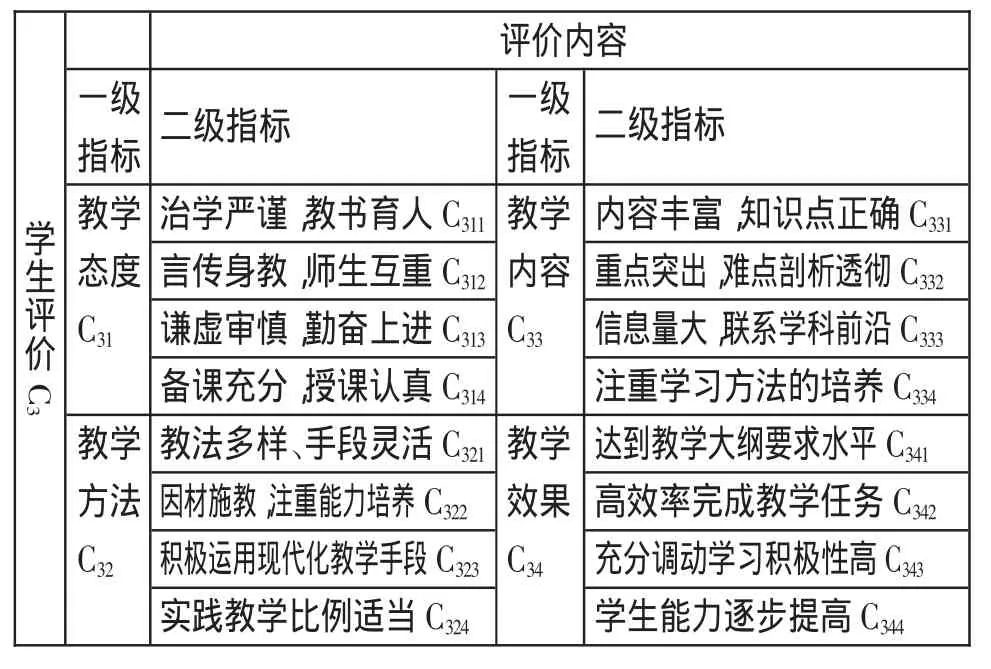
表2 学生评价子体系二级评价指标

我们以学生评价子体系为例，结合该子体系评价内容，逐步完成模糊综合评价过程。（表2）

1、根据表2构造评价指标判断矩阵，确定权重系数并作出一致性检验。

以学生评价中的“教学态度”为例，由专家决定判断矩阵：

同理，可计算其他指标权重集如下：

2、确定评语集、数值集、评价因素集，以及权重集，构造隶属度矩阵，利用模糊变换进行模糊综合评价。

评语集：V＝｛v1，v2，v3，v4｝＝｛优秀，良好，合格，不合格｝；

数值集：N＝｛N1，N2，N3，N4｝＝｛90，80，70，60｝。

现拟用100名学生结合学生各级学生评价指标进行综合评定，结果如表3所示。（表3）

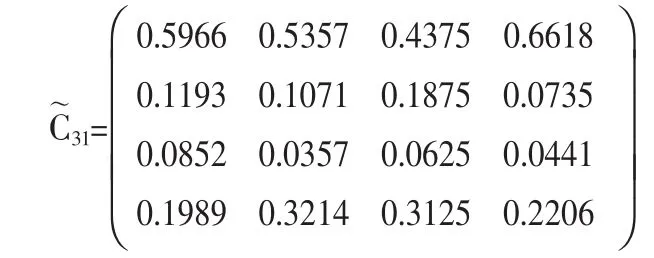
由表3可以得出学生评价关于各评价准则的隶属矩阵为：

对每个一级指标之下的二级指标，结合各自权重与隶属度进行模糊变换。归一化后导出二级指标的模糊评价矩阵。

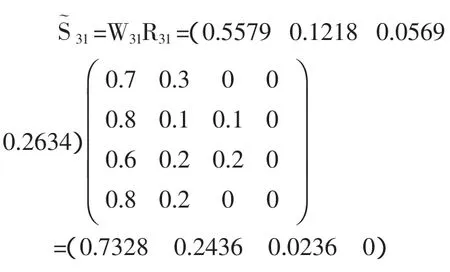
归一化后得：S31＝（0.73280.2436 0.02360）。

同理可计算：S32＝（0.46730.4255 0.10.0072），S33＝（0.69560.27240.0194 0.0126），S34＝（0.52370.4180.05830）。

将学生评价一级指标权重与一级模糊矩阵进行模糊综合运算：对进行归一化，得到学生评价子体系模糊综合评价向量：

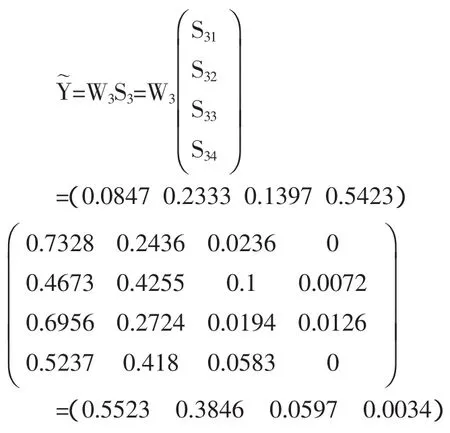
Y3＝（0.55230.38460.05970.0034）

3、各子体系评价结果的模糊综合分析。按照上述学生评价体系模糊综合评价结果的导出过程，我们可以类似的导出领导、同事两个子体系的最终评价向量，由于篇幅有限，具体过程不再赘述，不妨大胆假设：

Y1＝（0.27830.45360.25630.0118）

Y2＝（0.33450.48930.13810.0381）按照高校一般评价情况，我们设领导、同事、学生三方评价比重为3∶3∶4，即权重向量W＝（0.30.30.4），各评价子体系得到的综合评价矩阵为R＝（Y1Y2Y3），则最终模糊综合评价矩阵为：

由此可见，采用基于AHP的模糊综合评价得到的分数为82.3，该教师教学质量水平介于优秀与良好之间，有待提高。

四、结束语

利用基于AHP的模糊综合评价法所构建的教学质量评估体系，运用严谨的数学方法实现了定性问题定量分析的整个过程。从评价体系的应用过程以及结果分析，该体系具有如下几个特点：

1、在专家意见的基础之上，利用AHP确定各评价指标间的权重关系，在实现定性向定量分析转化的同时，较好的剔除过程中的主观成分。除此之外，判断矩阵的一致性检验保证了评价基础体系不会出现逻辑上的错误，从而使评价体系具有了更高的科学性、准确性、客观公正性。

2、教学质量各方面指标的优劣轻重本身就是一个模糊不清的概念，简单的逻辑运算不可能实现综合指标的交叉分析，更无法最终得到具体结果。而在AHP的基础之上，从分解比较到最后的判断综合，利用模糊综合运算处理这些模糊概念，能够利用数字和运算实现人类主观判断分析的全过程，从而使得最终结果更具有可靠性。

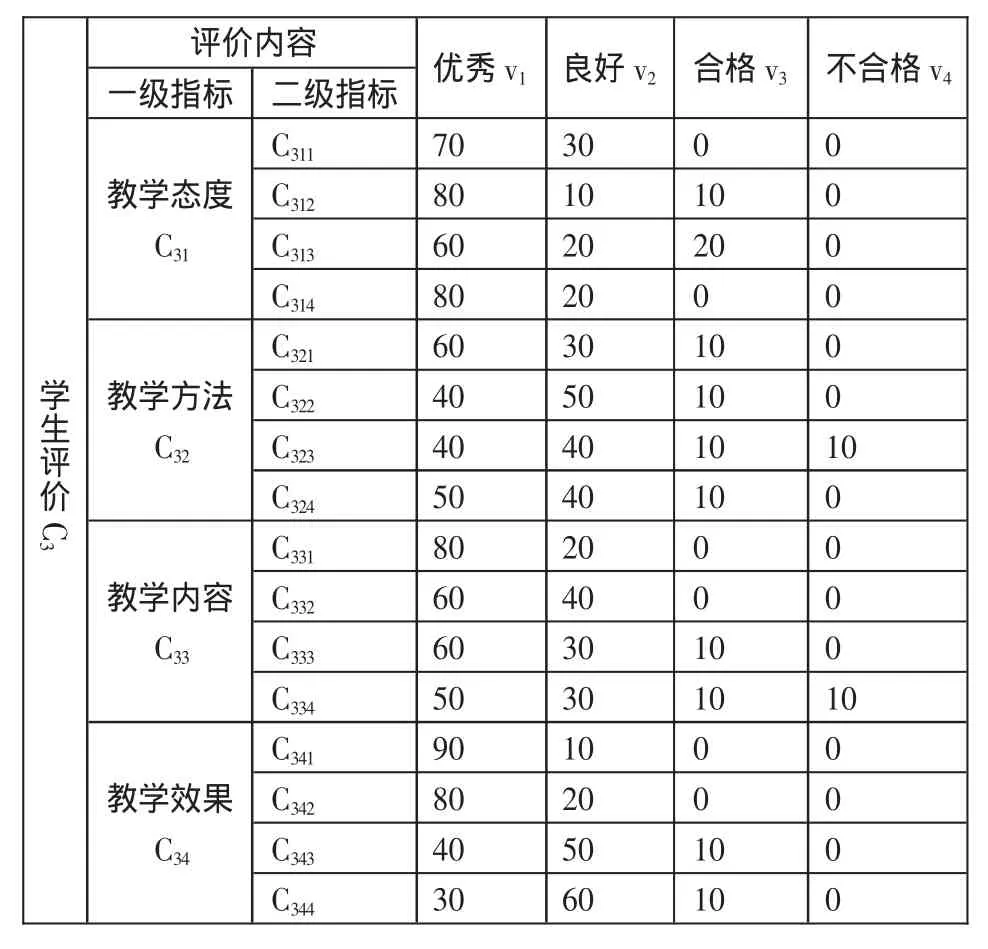
表3 100名学生对教师教学质量综合评测结果

3、评价体系结构严谨，规则简单，尽管数据相对繁多，但均可以利用数学软件实现全部计算分析过程，因此具有很强的可操控性。与此同时，根据模糊综合评价法的自身特点，评价体系中任何一个子体系，均可以得到单方面评价结果。这就意味着该体系既可以整体衡量教师教学质量，又可以对教师某方面单一指标做出评价，使教师既可以明确自身教学水平，又可以找出进一步提高的方向。可见，体系本身具有灵活的多用性，综合结果具有明确的导向性。

综上所述，基于层次分析法的模糊综合评价法的应用，使得教师教学质量评价体系具备了较强的科学性与实用性。随着教育教学改革的不断深化，该评价体系同样具有良好的应用前景以及推广价值。

[1]温田丁.试论模糊数学在教师教学质量评估中的应用[J].金融教学与研究，1995.3.

[2]邹舒，刘洪伟，曲晓波.多层次模糊综合评价法在评价教学质量中的应用[J].江苏技术师范学院学报（自然科学版），2009.15.1.

[3]姜启源，谢金星，叶俊.数学模型[M].北京：高等教育出版社，2003.

[4]严军花，王九群，李秋英.高校教师教学质量的多层次模糊综合评价模型及其应用[J].河北工程大学学报（社会科学版），2007.24.3.