图像粒LLE算法在人脸表情分析中的应用

吕思思， 梁久祯

（江南大学 物 联网工程学院，江苏 无 锡 214122）

人脸作为一个重要的生物特征，传递着重要的信息。一方面，因为其唯一性的特点，能够传达个体的身份信息，所以人脸识别是基于生物特征识别技术的身份认证中最主要的方法之一，与其他生物特征识别技术相比具有独特的优势。另一方面，人脸面部的表情又可以反映个体的思想感情和情绪状态，通过分析可以获知个体的内心态度和情感变化。对此许多研究机构和学者针对人脸展开了相关的研究工作，人脸表情的研究已成为模式识别和人工智能领域的热点。目前人脸表情研究在日常生活中有很好的应用前景，主要体现在对相关学科的促进、智能人机交互、心理状态分析、医疗诊断技术、图像实时传输、动画电影制作及娱乐产品开发等多个方面［1］。

在人脸研究中，因为简单、分类能力强等优点，基于线性子空间的方法已成为主流的特征提取方法。基于线性子空间分析的特征提取方法是根据一定的性能目标来寻找一个线性空间变换，将高维数据投影到低维线性子空间上，使投影后提取的特征数据更能满足目标要求，并且达到压缩原始数据维数的目的，为数据的描述提供方便，并降低计算的复杂度。在人脸特征提取中常用的线性子空间分析方法有主成分分析（Principal Component Analysis，简称PCA）［2］、线性判别分析（Linear Discriminate Analysis，简称 LDA）［3］、独立成分分析（Independent Component Analysis，简称ICA）［4］等。近年来的研究发现，人脸图像很可能位于一个非线性流形上［5－7］，基于流形学习（manifold learning）的人脸研究算法被提出。流形是线性子空间的一种非线性推广，是局部可坐标化的一个拓扑空间。流形学习本质上是一种非线性降维方法，旨在发现嵌入在高维数据空间的低维光滑流形。具有代表性的流形学习方法有局部线性嵌入 （Locally Linear Embedding，简称 LLE）［6］、拉 普 拉 斯 特 征 映 射 （Laplacian Eigenmaps，简称 LE）［8］、等 距 映 射 （Isometric Mapping，简称Isomap）［7］、局部保持投影（Locality Preserving Projections，简称 LPP）［9－10］等。

然而，由于人脸研究问题中的高维图像和大规模样本的关系，线性子空间法和流形学习算法均需要进行复杂的计算，制约着研究任务的快速性和有效性，这是该领域中研究的焦点和难点。人类在解决和处理大量复杂信息问题时，总是按各自的特征和性能将其分解为若干较简单的子问题或模块，然后对每个分割成的粒进行处理，降低了问题的难度和复杂度。粒计算［11］是基于不同层次的粒度上对问题进行观察、分析和求解，对于模式识别、图像处理、数据挖掘、知识工程等实际问题，粒计算是一种降低计算复杂度的有效方法。

本文针对人脸研究中高维数据的高计算复杂度问题，在粒计算的思想上，提出基于图像粒的LLE算法，旨在降低计算复杂度；并基于加权思想，实现图像粒LLE算法。在不同层次的粒度下分别实现LLE算法，分析粒计算方法的计算复杂度和图像信息丢失情况。在Frey人脸图像库上进行实验，结果表明，基于图像粒的方法降低了算法计算复杂度，提高了速率，并对图像信息的保持具有一定的有效性。

1 局部线性嵌入（LLE）算法

LLE算法能够实现高维输入数据点映射到一个全局低维坐标系，同时保留了邻接点之间的关系，使降维的数据保持原有的拓扑结构。算法认为在流形上小的每个局部是一个局部欧式空间，因此邻域内数据的结构是线性的，每个样本点及其近邻样本之间是线性关系，从而一个样本点可以用其近邻样本的线性组合来重构。通过最小化重构误差，可以得到近邻样本之间的线性表示权重，其中蕴含着数据集的局部领域的结构信息。LLE算法根据权值矩阵，在低维数空间中构造出与原样本集具有类似邻域结构的嵌入向量集合，从而保证了原样本集中的近邻样本的嵌入向量仍然是近邻，且嵌入空间中的邻域结构与原样本集合的邻域结构保持相似。

1.1 LLE算法步骤

LLE算法的具体步骤为：

（2）重构权值矩阵。每个样本点xi及其领域点xij之间的重构权值为wij，定义误差函数为：

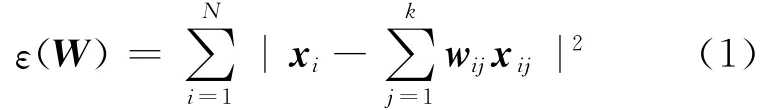
且满足条件：

通过极小化（1）式来实现重构权值wij的构造。

在约束条件（2）式下，（1）式中的误差函数可写为：

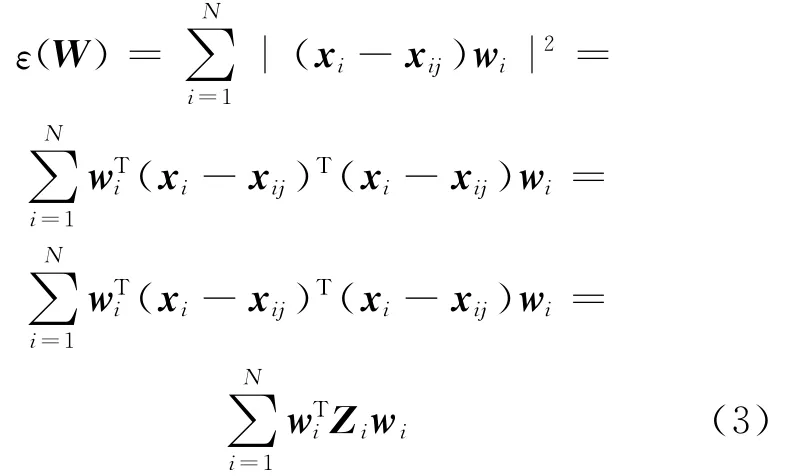
其中，Zi＝（xi－xij）为第i个样本点xi的局部协方差矩阵；w＝［wi1，wi2，…，wik］T为第i个样本点的局部重建权值。

求解 （ 3）式是一个约束最小乘方问题，可用Lagrange乘子法，则有：即可求得wi，（4）式中c通常取1。

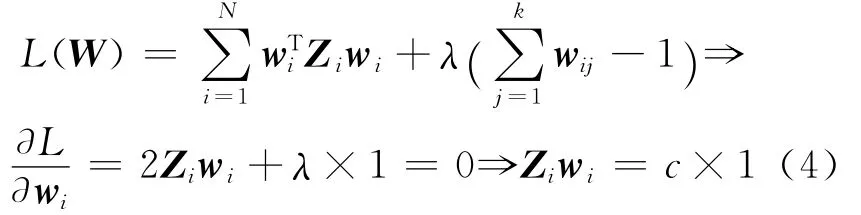
（3）计算低维嵌入。将所有的样本点映射嵌入到低维空间中，映射嵌入满足的条件为：

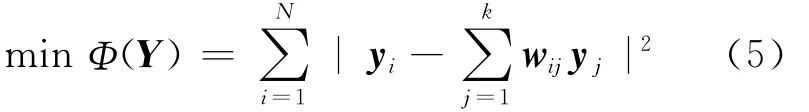
其中，yi为xi的输出量；Φ（Y）为损失函数。

优化输出向量Y满足以下2个条件：

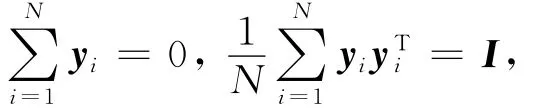
其中，I为单位矩阵。wij（i＝1，2，…，N）可存储在N×N的稀疏矩阵W 中 ，当xj为xi的近邻点时，Wi，j＝wij；否则，Wi，j＝0。用Wi表 示W 矩 阵的第i列，Ii表示N×N单位矩阵的第i列，输出向量Y＝［y1，y2，…，yN］。（5）式可写为：

其中，M＝（I－W）（I－W）T。结合约束条件，利用Lagrange乘子，则有：

要使损失函数（5）式达到最小，取Y为M 的最小d（d＜D）个非零特征值所对应的特征向量。通常最小特征值几乎为0，因此取第2～（d＋1）间的特征值所对应的特征向量作为输出结果Y。

1.2 算法复杂度分析

（1）选取邻域计算复杂度为O（DN2），近邻数k通常是较小的数，有k≤D。

（2）重构权值矩阵的计算复杂度为O（（D＋k）k2N）。

（3）由于矩阵M具有很强的稀疏性，计算d维嵌入的计算复杂度为O（dN2）。

该算法时间复杂度为：

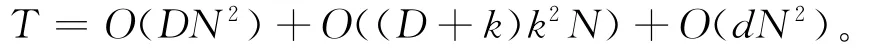
通常，映射嵌入的维数d是一个较小的数，显然有d＜D，故LLE算法复杂度近似为：

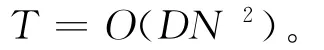
图像的最基本单位是像素，许多图像处理方法都是建立在像素这个层次上。而在很多实际问题中，并不需要完全以像素为单位来进行处理，只需对图像保持一定的信息。对于包含1 000张128×128的人脸图像的样本数据，每幅图像维数D＝128×128＝16 384，直接应用LLE算法时，计算复杂度T＝O（DN2）＝O（1010）；若对图像按8×8大小分块，每个块作为一个粒进行处理，则图像维数降低为D＝16×16＝256，计算复杂度T＝O（108）。图像粒是一个降低计算复杂度的有效方法。

1.3 加权预处理

在人脸研究中，针对人脸图像的不同区域研究的重点各不相同。人脸表情的研究分析中，人脸的眼睛、嘴巴等区域作为较重要分析部位。在选择近邻点中，在计算2个样本图像之间的欧式距离时，先对图像进行加权预处理，给定每个像素点一个权值，增大较为重要部位的像素点的权重，计算结果增大了对重要部位的像素点的相似度计算，对近邻点的选择产生一定的变化。

每个样本图像xi＝［x1i，x2i，…，xDi］T，其权值计算公式为：

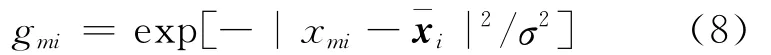
其中，m＝1，2，…，D；

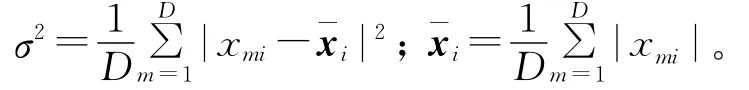
每个像素点进行如下加权：

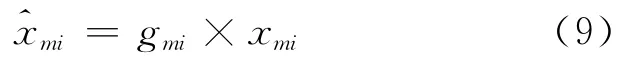
2 图像粒

粒计算融合了模糊集、粗糙集及人工智能等领域的研究成果，其思想源于有关模糊集的信息粒化研究［12］。所谓信息粒是指人类在解决和处理大量复杂信息问题时，按各自的特征和性能将其分解为若干较简单的子问题或模块，每个分割成的块被看作一个粒，而这种处理信息的过程即为信息粒化。粒计算是在解决问题过程中运用粒（granule）概念的一种理论和方法，基本单位是粒，一个粒可以看作是由内部属性描述的个体元素的集合［13］，这些个体元素因为相似性、不可区分性及一致性等结合在一起。不同的粒化准则生成不同的粒层次和粒结构，在不同的粒层次下解决问题时往往会产生具有不同特性的方法。

粒度是一个物理学概念，它在计算机界则被用作“信息粗细的平均度量”。信息粒度的提出，主要是因为很多专家和学者都认识到人工智能在处理现实世界的问题时，常常采用从不同层次观察问题的策略。对于一个问题，有时需要在不同的粒度层次上对问题进行求解，因此需要研究不同粒度世界的关系。

设R表示由论域X上一切等价关系组成的集合，可以定义如下等价关系，即粒度的“粗”和“细”。

定义1 设R1，R2∈R，如果对于任意x，y∈X，都有xR1y⇒xR2y，那么称R1比R2细，记作R1≤R2。

定义2 假设存在一个概念φ，属于概念φ的所有元素记作φ的意义集m（φ），表示为m（φ）＝｛x∈U，x｜≈φ｝，其中U表示论域；｜≈表示一种公式可满足性符号，将m（φ）称作一个粒。

对于一幅大小为h×w的图像，I＝Ih×w表示该图像的所有像素；图像中任意一个像素或块，记作b＝［h1，h2］×［w1，w2］，显然有0≤h1＜h2＜h且0≤w1＜w2＜w；则Ib即为一个粒：m（Ib）＝｛（i，j）∈b⊆［0，h）×［0，w）｝，最细的粒是像素层次上的，即只含有1个像素，最粗的粒是包含整幅图像所有像素的块。

定义3 粒m（φ）的大小定义为：

L（m（φ））＝ Card（m（φ））／Card（U） （10）其中，Card（m（φ））表示m（φ）中包含的元素个数；Card（U）表示论域U的元素总数。

在一幅大小为128×128的图像I中，若Ib为I中的一个块，b＝［0，3］×［0，3］。由定义2知Ib为 一 个 粒，大 小 为L（m（Ib））＝Card（m（Ib））／Card（I）＝（4×4）／（128×128）＝1／1 024。对于整幅图像，最细的粒大小为L（m（Ifine））＝1／（128×128）＝1／16 384，最粗的粒大小为L（m（Icoarse））＝1。

定义4 将图像I分块b1，b2，…，bt，每块为一个粒m（Ib），每个粒中所有像素的均值为E1，E2，…，Et，这组均值的方差为σ。定义图像粗糙度r（I）＝e－σ，显然有0＜r（I）≤1。

对于一幅图像，所分的块越小，即粒越细，σ越大，e－σ越小，即图像粗糙度r（I）越小，信息丢失量越少；反之，粒越大，图像越粗糙，即丢失的信息量越多。

定义5 假设I1、I2为2个相邻层次上的图像粒，不妨令L（m（I1））＜L（m（I2）），定义图像粒差异D（I1，I2）＝r（I1）－r（I2）。

3 图像粒实验

选择Frey人脸数据库进行实验，该数据库包含同一人在一段视频中截取的1 965幅不同表情、姿态的图像，每幅图像大小为20×28像素，每像素256灰度级，这样每幅人脸图像为560维灰度图像。部分图像如图1所示。

图1 Frey人脸数据库中部分图像

3.1 图像粒LLE实验

人脸数据库中图像应用LLE算法降维处理后的分布情况如图2所示。

图2 Frey库图像在像素粒度上应用LLE的二维线性嵌入

人脸图像映射到由LLE算法的前2个坐标所描述的二维平面上，一些有代表性的面孔显示在对应数据点的旁边。由图2可以看出，人脸图像有2个明显的变化方向。从上到下有明显的人脸角度的变化，即从面向左侧、正面、面向右侧的转变；从左到右有明显的人脸表情的变化，即左边的闭着嘴巴的不开心的表情，逐渐向右边转变为开心的微笑着的表情。

按图像粒的方法进行实验。对图像分别以2×2、4×4大小的图像粒进行分块，计算每个粒中所包含的所有像素的均值，则每幅人脸图像转变为140维、35维灰度图像，对图像原始的高维数据进行了降维。1 965幅人脸图像应用图像粒预处理并应用LLE算法降维后的分布情况如图3所示。

将人脸图像映射到由LLE算法的前2个坐标所描述的二维平面上，部分数据点的边上显示对应的原始人脸图像。实验结果与图2相比，图3中人脸图像的整体分布形状上有变化，而人脸的连续性变化情况没有明显改变，仍然维持在从上到下角度的变化、从左到右的表情的变化趋势。但随着粒的增大，图像信息丢失程度增加，图像集中程度高，区分不明显。

图3 Frey库图像应用图像粒LLE的二维线性嵌入

算法的计算复杂度问题，体现在实验的运行时间上。以像素为粒进行实验时，从读取图像开始到LLE算法结束为运行所用时间；以图像粒进行实验时，运行时间还包括了对图像的分块以及计算每个粒中所有像素均值所用的时间，总的运行时间有所变化。在不同粒度大小下实验的运行时间见表1所列。

表1 不同图像粒下实现LLE的时间 s

表1中k为选择的近邻个数。由表1可以看出，对每个选择的近邻数k，运行时间随着图像粒的增大而减少，降低了计算复杂度。

虽然实验减少了运行时间，提高了速度，但以图像粒方法对图像进行处理时，图像的信息有丢失。随着粒的增大，二维嵌入中分布的点（即对应的图像）的区分却不明显，是因为随着粒的增大，图像的信息损失程度增大，一些细节上的差别信息丢失。

下面分析针对不同图像粒大小进行实验时人脸图像信息量的情况。根据定义4，计算每张图像在不同大小的图像粒处理方法时的图像粗糙度。图1所示的9张人脸图像的粗糙度、信息熵及粒差异见表2所列。从表2可以看出，随着图像粒的增大，图像粗糙度增加，即图像变得越粗糙，损失的信息量越多；随着图像粒的增大，图像信息熵减少；随着图像粒的增大，相邻层次上的图像粗糙度之差变大，图像变粗糙的程度越快，图像信息的损失越严重。

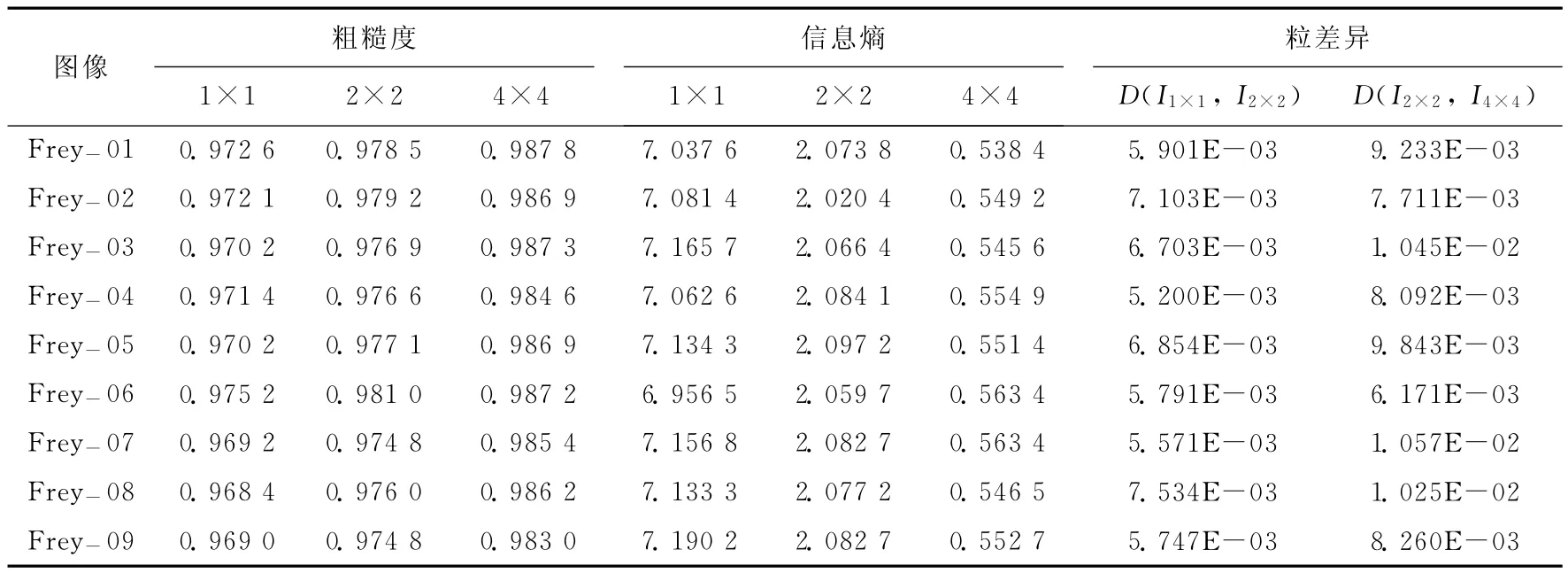
表2 不同图像粒下Frey库图像应用LLE的粗糙度、信息熵和粒差异

3.2 加权预处理的图像粒LLE实验

将Frey人脸数据库中图像分别以1×1、2×2、4×4大小的图像粒进行分块，计算每个粒中所包含的所有像素的均值，对图像原始的高维数据进行降维，然后应用加权预处理的图像粒LLE算法，降维处理后映射到前2个坐标所描述的二维平面上，人脸图像分布情况如图4所示，数据点的旁边显示的是对应的面孔。

图4 Frey库图像在不同粒度上应用加权预处理LLE的二维线性嵌入

由图4可以看出，人脸图像有2个明显的变化方向，从上到下人脸角度的变化和从左到右人脸表情的变化。纵向变化上，人脸从面向左侧、到正面、最后面向右侧；横向变化中，人脸表情从左边的闭着嘴巴不开心逐渐向右边转变为开心微笑的表情。在像素粒度和2×2粒度变化下，人脸图像分布维持上述连续变化规律，但随着粒增大，图像信息损失程度增大，一些细节上的差别信息丢失，在4×4粒度下图像集中度高，中间部分很难进行区分。和3.1的实验相比，在对应粒度下，本节实验的二维线性嵌入人脸分布较为明显。

在像素粒度上进行实验时，从读取图像到算法结束为运行所用时间；以图像粒进行实验时，运行时间包括对图像的分块、计算每个粒中所有像素均值以及计算图像像素权值所用的时间，实验结果见表3所列，由表3可看出，运行时间随着图像粒的增大而减少，降低了计算复杂度。

表3 不同图像粒下实现加权预处理LLE的时间 s

根据定义4、定义5计算图1中的9张人脸图像在不同大小的图像粒处理时的图像粗糙度、信息熵和图像粒差异，见表4所列。从表4可看出，随着图像粒的增大，图像粗糙度增加，即图像变得越粗糙，损失的信息量越多；相邻层次上的图像粗糙度之差变大，图像变粗糙的程度越快，图像信息的损失越严重。这与图像信息熵的计算结果一致。

表4 不同图像粒下Frey库图像应用加权预处理LLE粗糙度、信息熵和粒差异

4 结束语

本文提出了一种基于粒计算思想的局部线性嵌入方法，首先以粒度大小对图像进行分块处理，随后进行LLE算法。从Frey人脸库上的实验结果分析可知，该方法对人脸图像信息的保持具有一定的有效性，能对姿态和表情进行区别和分类；同时，对图像实现了数据降维，降低了计算复杂度。从数据可看出，随着图像粒度的增大，运行时间减少，而图像粗糙度增加，这样可以选择一个最佳的粒度大小，既保持了一定的图像信息量，又减少运行时间，提高效率。

［1］ 朱明旱.基于流行学习的人脸表情识别研究［D］.长沙：中南大学，2009.

［2］ Turk M A，Pentland A P.Face recognition using eigenfaces［C］／／Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition，1991：586－591.

［3］ Belhumeur P N，Hespanha J P，Kriegman D J.Eigenfaces vs.Fisherfaces：recognition using class specific linear projection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（7）：711－720.

［4］ Bartlett M S，Movellan J R，Sejnowski T J.Face recognition by independent component analysis［J］.IEEE Transactions on Neural Networks，2002，13（6）：1450－1464.

［5］ Tenenbaum J B，Silva V D，Langford J C.A global geometric framework for nonlinear dimensionality reduction ［J］.Science，2000，290（5500）：2319－2323.

［6］ Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding［J］.Science，2000，290 （5500）：2323－2326.

［7］ Shashua A，Levin A，Avidan S.Manifold pursuit：a new approach to appearance based recognition ［C］／／Proceedings of 16th International Conference on Pattern Recognition，2002：590－594.

［8］ Belkin M，Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation［J］.Neural Computation，2003，15（6）：1373－1396.

［9］ He Xiaofei，Niyogi P.Locality preserving projections［C］／／Proc of the Conf on Neural Information Processing Systems.Vancouver，Canada，2003：153－160.

［10］ He Xiaofei，Yan Shuicheng，Hu Yuxiao，et al.Face recognition using Laplacianfaces［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（3）：328－340.

［11］ Lin T Y.Granular computing，announcement of the BISC special Interest group on granular computing［EB／OL］.［1997－08－09］.http：／／www.cs.uregina.ca／～yao／GrCl.

［12］ 张燕平，罗 斌，姚一豫，等.商空间与粒计算：结构化问题求解理论与方法［M］.北京：科学出版社，2010：144－156.

［13］ 张 钹，张 铃.粒计算未来发展方向探讨［J］.重庆邮电大学学报：自然科学版，2010，22（5）：538－540.