负偏心对钢管-插板K型节点承载力的影响
王蔚佳,刘红军,李正良
(重庆大学土木工程学院,重庆 400045)
负偏心对钢管-插板K型节点承载力的影响
王蔚佳,刘红军,李正良
(重庆大学土木工程学院,重庆 400045)
对主管规格为219 mm×6 mm有负偏心作用的1/4加肋钢管插板连接的极限承载力进行了试验研究,根据试验结果提出了等效受力模型,在此基础上研究了有负偏心的1/4(1/2)和全环形加强板钢管插板连接的K型节点的主管轴力、主管管壁弯矩和剪力三者之间的相互关系,并利用有限元软件分析了各参数对节点极限承载力的影响,在此基础上提出了此类节点的建议公式并与试验结果进行了比较。结果表明:建议公式表面看是反映两两之间的相互关系,实际上是反映了主管轴力、主管管壁弯矩和剪力三者之间的关系,建议公式能较好的估算节点承载力的上限值。
负偏心;极限承载力;插板连接;等效受力模型
钢管塔构造中斜材轴心线交于主材轴心线造成节点板尺寸很大,节点连接负偏心可以减小节点板尺寸,减小迎风面积。然而,在目前的设计中[1-8],由于其复杂的受力形式,插板连接的极限承载力建议公式仅适用于有限的情况。许多学者提出的建议公式都是针对无偏心的情况。Kurobane[9]通过试验研究了在轴力和弯矩作用下T型和X型节点的极限承载力;Wardenier、Packer等[10-12]针对单插板和双插板连接提出了建议公式;Ariyoshi等[13]确立了圆钢管与插板连接在简单荷载作用下的试验结果和数值分析结果的数据库。但他们都没有考虑主管和支管上荷载的联合作用效应以及偏心对极限承载力的影响。
Kim等[14-16]对无环形加强板情况下偏心对极限承载力的影响进行了初步研究。由于K型节点受力的复杂性,尤其是钢管-插板连接的K型节点受力更加复杂,所以关于K型节点的极限承载力公式很少。为进一步研究负偏心对K型节点承载力的影响,笔者通过试验及有限元软件对负偏心钢管塔节点承载力进行了研究,提出了计算此类节点的建议公式。
1 试验研究
1.1 试验试件及加载装置
试验研究4种不同插板连接的节点,主要考察偏心距对主管极限承载力的影响和局部应力集中现象。各试件参数见表1。为了防止节点板发生破坏,节点板的厚度都比较大。试验主要研究不同参数情况下节点的破坏类型并比较偏心距对主管承载力的影响。插板连接构造如图1所示,加载装置如图2所示,环板的形式如图3所示。
1.2 加载方案
试验加载为单向加载。主管与支管同步加载,1#千斤顶(拉)和3#千斤顶(压)分别与支管相连,2#千斤顶与主管相连,见图2。支管荷载先以每级荷载增量为25 k N逐级加载至250 k N,而主管荷载以每级荷载增量为40 k N逐级加载至400 k N;后支管以每级荷载增量为10 k N逐级加载至350 k N,而主管荷载以每级荷载增量为20 k N逐级加载至600 k N;最后支管以每级荷载增量为5 k N逐级加载至支管受压承载力而停止加载,而主管荷载以每级荷载增量为5 k N逐级加载至构件破坏。此时主管的荷载即为主管的极限承载力,每级加载停顿1 min后继续加载。

图1 插板连接构造图

图2 试验装置图
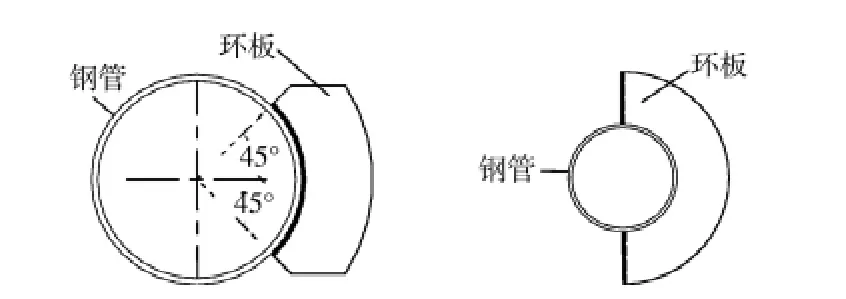
图3 1/4(1/2)环板连接构造图
1.3 试验结果
试验结果表明:构件发生整体失稳先于局部屈曲。主要原因在于主管长径比较大,属于压弯构件,整体很容易失稳。由于主管长径比较大,因此整体失稳起主要控制作用,负偏心加速了整体失稳,降低了主管的承载能力。因此负偏心对整体失稳不利。表2为不同支管荷载作用下的主管承载力。
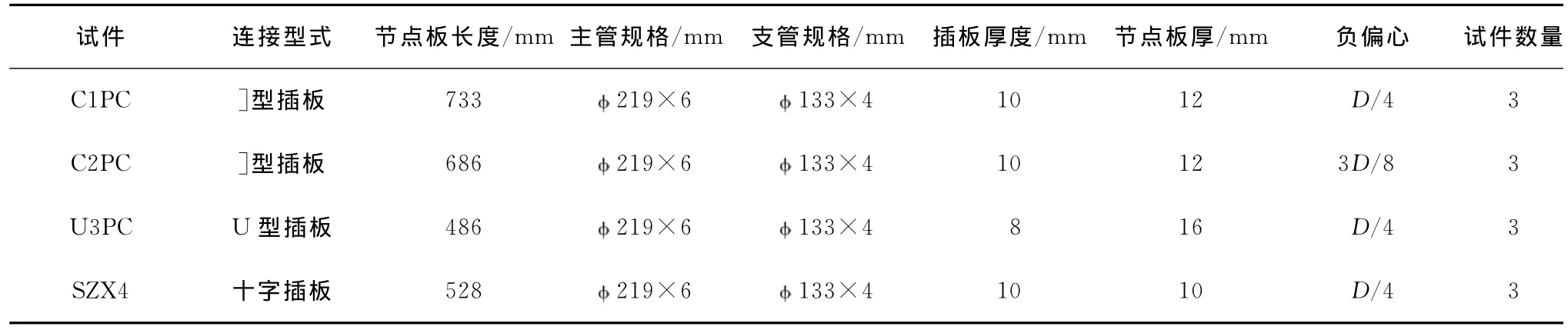
表1 各试件参数

表2 试验结果
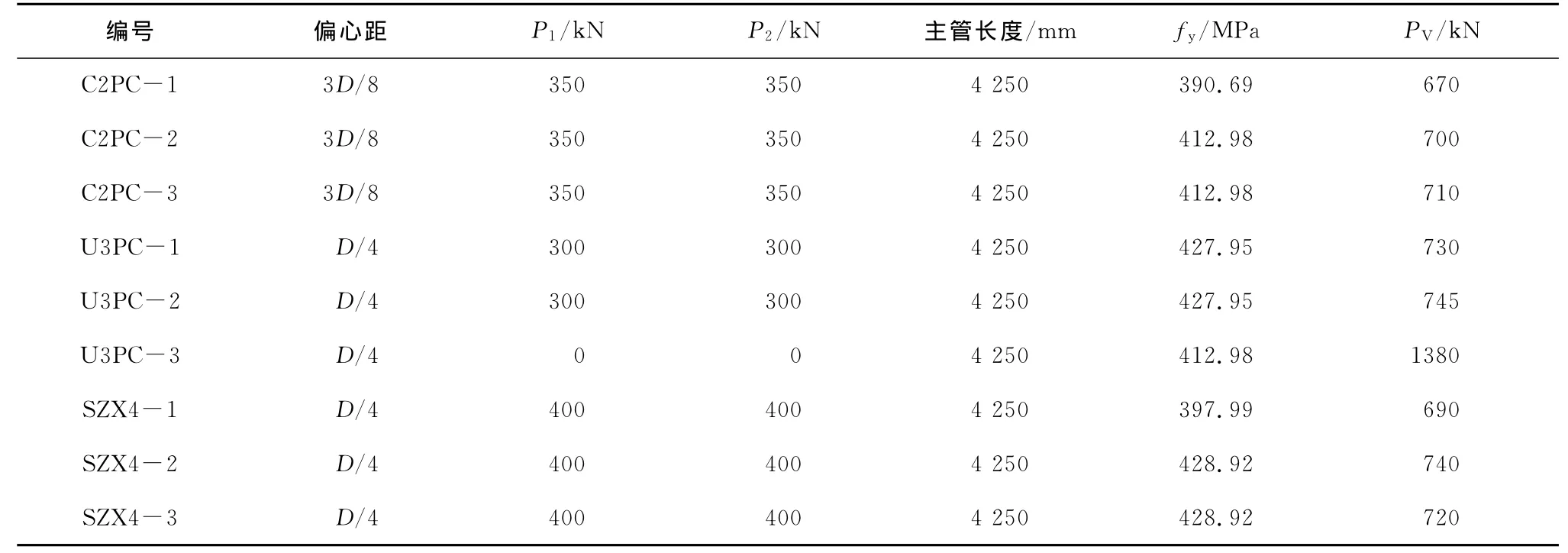
续表2
2 节点等效受力模型
在输电塔架结构中,K型节点经常用于主材与斜材的连接,见图4。通过对K型节点受力分析发现,支管荷载对主管管壁的作用可以分解成弯矩和剪力,如图5所示。

图4 K型节点的构造图

图5 节点等效受力模型
既然中空圆形截面在外荷载作用下更容易发生局部变形,那么K型节点构造的几何尺寸就应该通过精确分析确定。但由于受力性能的复杂性,目前的设计规范没有详细的公式,因此,基于负偏心作用的K型节点的极限承载力的研究很有必要。
笔者利用有限元程序ANSYS对K型钢管-插板连接节点进行弹塑性大挠度分析,研究节点的应力分布情况和极限承载力,其模型见图6。模型分析中采用4节点四边形壳单元shell181来模拟节点板、钢管和加强板。边界条件如图7所示,主管一端按固定支座考虑,另外一端为仅有沿主管轴线方向位移的固定支座。两支管端部边界为滑动铰支座,仅允许沿管轴线方向有位移,约束径向位移。加载方式与试验相同。有限元分析时,材料选取Q345,其屈服强度fy=345 MPa,在考虑材料非线性时,从材料的单轴拉伸试验曲线中得到,其应力-应变关系如图8所示。弹性模量E=2.06×105MPa,泊松比取0.3,忽略自重的影响。表3即为试验结果与有限元结果的比较。从表3可以看出,计算结果与试验结果较接近,吻合性较高,具有较好的适用性。
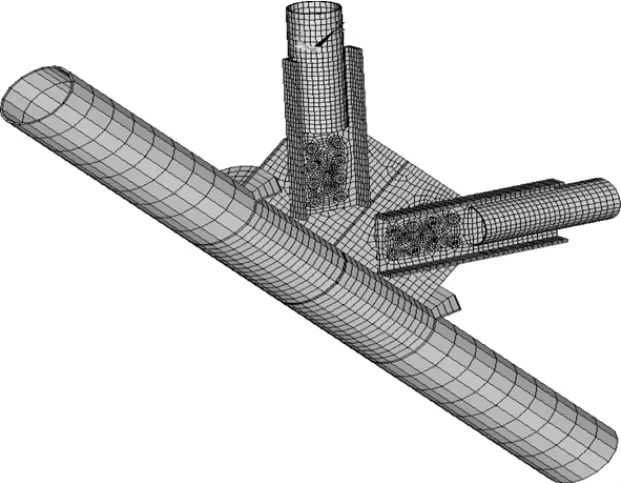
图6 有限元模型
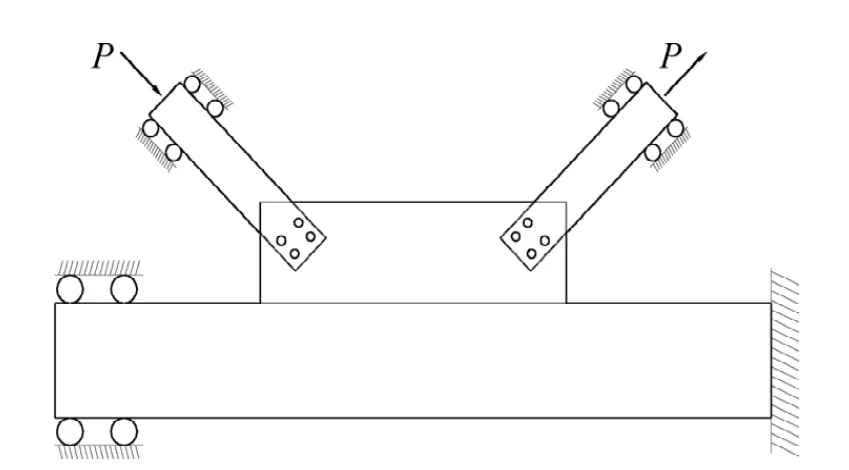
图7 节点加载示意图
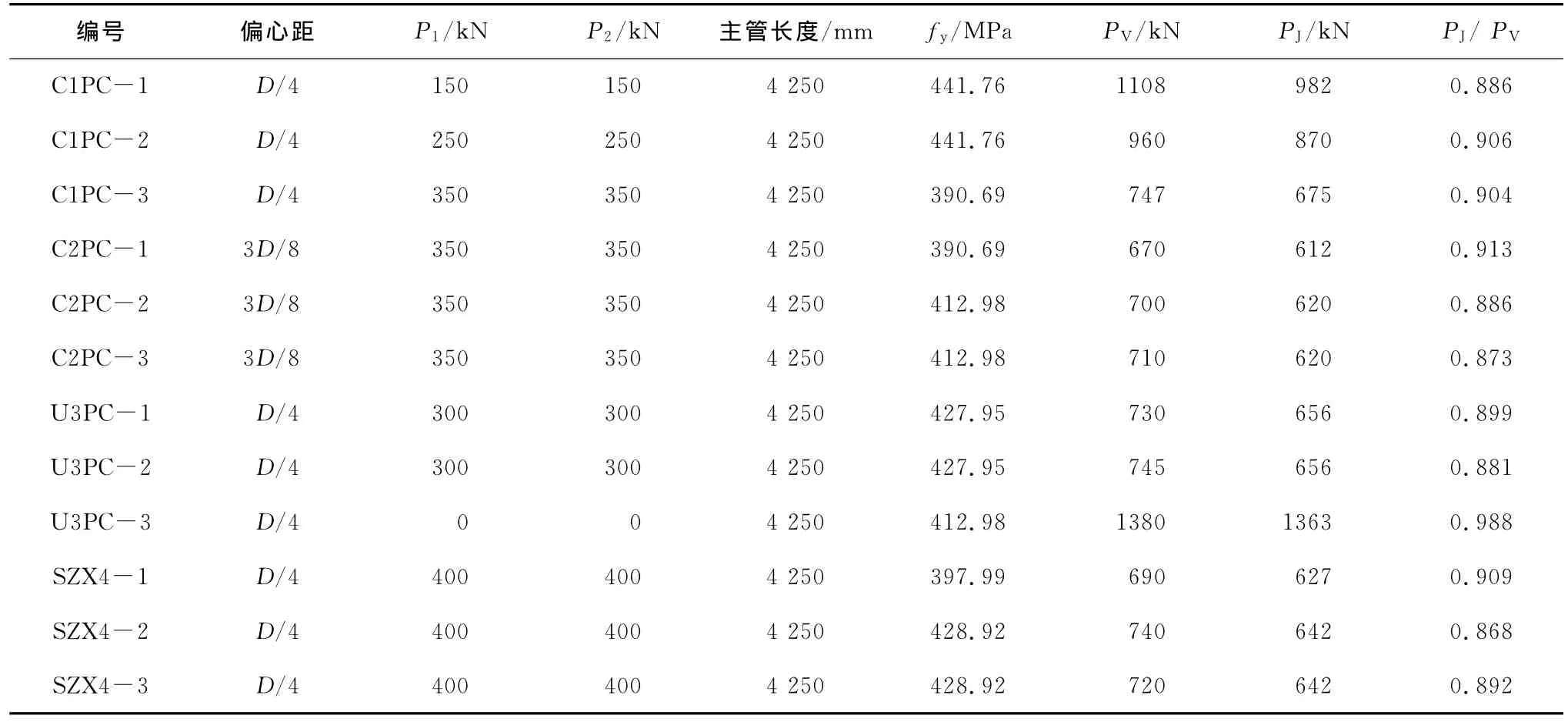
表3 试验结果

图8 材料应力-应变关系模型
3 参数对承载力的影响
通过有限元软件对1/4(1/2)和全圆环加强板K型节点各参数对节点承载力的影响进行了分析,其关系曲线如图9所示。
从图9可以看出,节点在无偏心的情况下,主管直径D和主管壁厚t对节点承载力有显著影响。节点承载力随着节点板高度B的增加变化甚微,几乎不变;主管管壁弯矩(M=Py·B)随着环形加强板高度和厚度的增加而增加,其变化趋势较平缓。在偏心距为D/2的情况下,主管管壁剪力随着主管直径的增加而线性增加;随着主管壁厚的增加也呈线性增加趋势;而节点板高度、加强板高度和加强板厚度对主管管壁剪力的影响甚微,几乎不变,表明在偏心距为D/2时剪力只对主管发生局部屈曲时产生作用。
4 节点承载力实用计算方法
通过各参数对主管管壁弯矩、剪力和主管轴力的影响曲线可以看出,主管管壁弯矩、剪力和主管轴力在负偏心过程中存在相互作用的关系,对有限元分析结果进行拟合,得到在无偏心、偏心D/2时节点主管轴力与横向力之间的关系式和在负偏心过程中主管管壁剪力与等效横向力之间的关系式,见图10~图12。
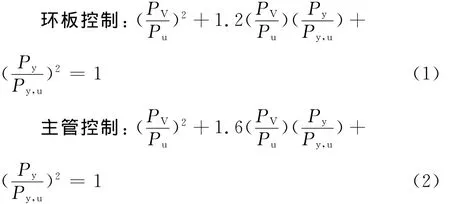
式(1)、(2)是无偏心时主管轴力与等效横向力的关系式。式中PV为主管轴力;Py为有轴力无偏心时节点的等效横向力;Pu为有轴力时节点的等效横向力;Pu=fy·A;fy为主管屈服强度;A为主管截面积;Py,u为无轴力时节点的等效横向力。
负偏心距为D/2时主管轴力与主管管壁剪力之间关系式:

式中:Qw,u为无轴力时主管管壁剪力;Qu为有轴力时主管管壁剪力。
节点从无偏心到偏心D/2的过程中,主管管壁的弯矩和剪力在不断变化。在主管轴力、主管管壁弯矩和剪力的作用下节点将发生局部屈曲。根据有限元分析结果进行拟合得到节点等效横向力与主管管壁剪力之间的关系曲线见图12。


图9 节点各参数对节点承载力的影响曲线图
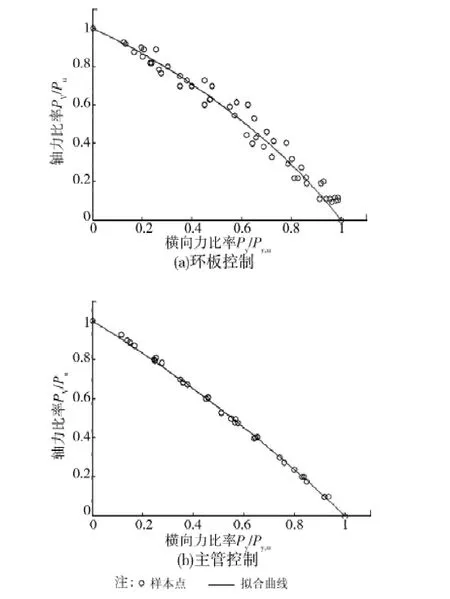
图10 主管轴力与等效横向力关系曲线图(无偏心)
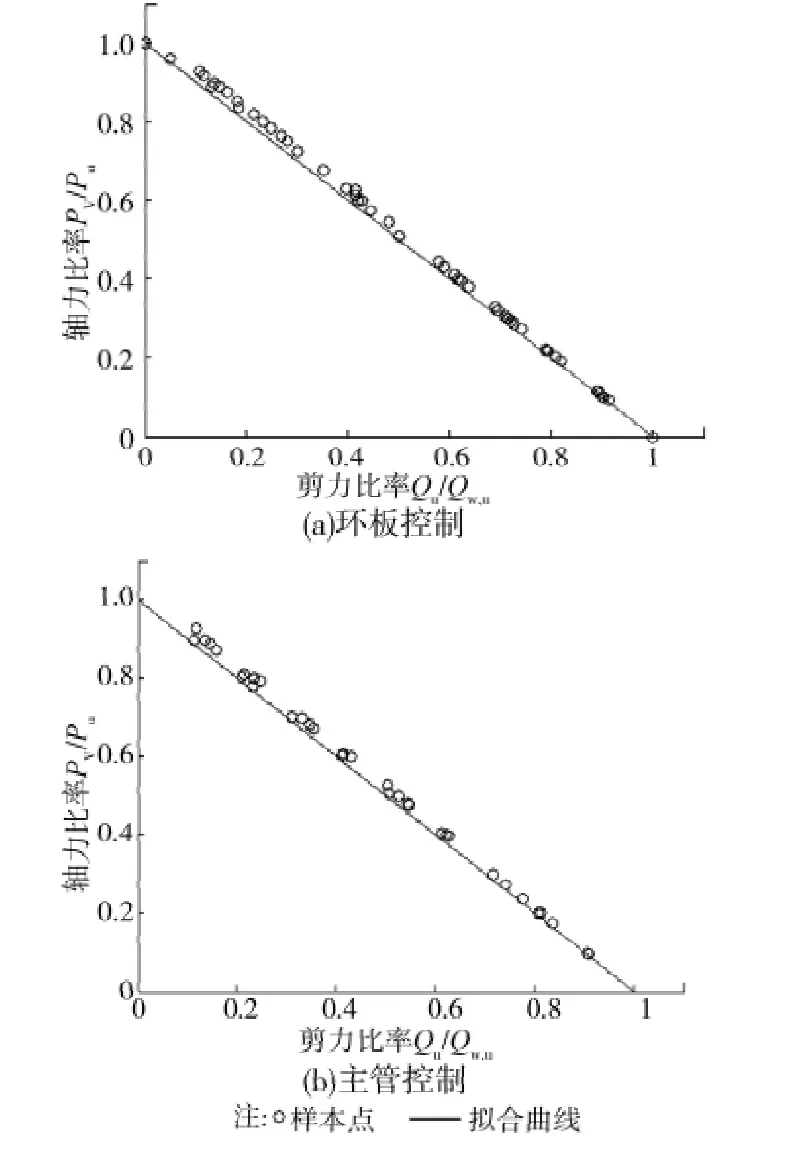
图11 主管轴力与主管管壁剪力关系曲线图(偏心D/2)
环板控制:


图12 主管管壁剪力与等效横向力关系曲线图
式(5)、(6)是负偏心过程中主管管壁剪力与节点等效横向力的关系式。Pa为有轴力有偏心时节点的等效横向力;Qw为有轴力偏心时主管管壁剪力。
从式(1)~(6)可以看出:在节点的几何尺寸确定的情况下,先要判断出无轴力无偏心时节点的承载力是由主管控制还是由环板控制。在负偏心距为D/2时,主管控制和环板控制的主管管壁剪力与主管轴力的关系式是相同的。因为在负偏心距为D/2时节点的破坏模式都相同,即节点下端主管发生局部屈曲。在负偏心过程中,承载力由主管控制和由环板控制的节点的主管管壁剪力与等效横向力的关系式形式不一样。承载力由主管控制的节点主管管壁剪力与等效横向力的关系表达式为线性关系。在已知主管轴力的情况下,将其值分别代入无偏心时节点等效横向力与主管轴力的关系式和偏心D/2时主管管壁剪力与主管轴力的关系式中,得到Qu和Mu(Mu=Py·B)。此时,根据弯矩和剪力的关系式就能得到在不同的偏心距时的主管管壁弯矩和剪力。反之,知道弯矩,就能求出偏心距,从而算出此时主管的轴力。3个等式还可以检验力的相互组合是否安全,以便用于指导设计。
为了验证文中算式的适用性,其计算结果与文献[16]结果进行对比分析见表4。

表4 建议式计算结果与文献[16]试验结果比较
从表4可以看出,建议式计算值与试验结果最大相差约9%,吻合较好,建议式具有较好的适用性。
5 结论
1)根据等效模型提出的有环形加强板的钢管-插板连接K型节点承载力建议式反映了负偏心过程中主管轴力、主管管壁弯矩和剪力之间相互关系。建议式表面看是反映两两之间的相互关系,实际上反映了主管轴力、主管管壁弯矩和剪力三者之间的关系,通过建议式能估算节点承载力的上限值。
2)根据弯矩和剪力关系式能得到在不同的偏心距的主管管壁弯矩和剪力。反之,知道弯矩,能求出偏心距,从而算出此时主管的轴力。根据主管轴力、主管管壁弯矩和剪力三者之间的关系式可以检验其相互组合是否安全。
[1]Architectural Institute of Japan.Recommendations for the designed fabrication of tubular structures in steel[S].Tokyo:Japanese Steel Construct,1990.
[2]The Japanese Steel Tubular Association.Electricity transmitting steel tubular tower manufacture norm[S].Tokyo:Japanese Steel Construct,1985.
[3]KEPCO.Specification for electric transmission tower design[S].Tokyo:Japanese Society Steel Construct,1991.
[4]陈以一,赵必大,王伟,等.平面KK型圆钢管相贯节点平面外受弯性能研究[J].土木工程学报,2010,43(11):8-16.
CHEN Yiyi,ZHAO Bida,WANG Wei,et al.Behavior of unstiffened CHS KK-joints under cyclic out-of-plane bending[J].China Civil Engineering Journal,2010,43(11):8-16.
[5]孙波,程睿,郭薇,等.空间钢管-板XX型节点静力性能参数分析[J].土木建筑与环境工程,2010,32(4):12-18.
SUN Bo,CHENG Rui,GUO Wei,et al.Parametric analysis of the static behavior of gusset plate to CHS XX-joints[J].Journal of Civil,Architectural &Environmental Engineering,2010,32(4):12-18.
[6]郑军.空间X+双KK型圆钢管焊接节点静力性能试验研究[J].太原理工大学学报,2011,42(1):83-87.
ZHENG Jun.Experimental study on static behavior of space X+double KK-joints[J].Journal of Taiyuan University of Technology,2011,42(1):83-87.
[7]余志祥,闫雁军,赵世春.K型外套强化矩管桁架节点滞回性能与恢复力模型[J].四川大学学报:工程科学版,2010,42(6):66-72.
YU Zhixiang,YAN Yanjun,ZHAO Shichun.The hysteretic behavior and restoring force model of the K-shape outer sleeve RHS joints[J].Journal of Sichuan University:Engineering Science Edition,2010,42(6):66-72.
[8]Meng X D,Chen Y Y,Wang W,et al.Experimental research on hysteretic property of unstiffened tubular X-joints under quasi-static out-of-plane bending[C]//Proceedings of Eleventh East Asia-Pacific Conference on Structural Engineering&Construction,Taipei,2008:442-443.
[9]Kurobane Y.New developments and pratices in tubular joint design[C]//International Organizations Institution Welding.Tokyo:Annual Assembly,1981: 197-223.
[10]Wardeneir J.Hollow section joints[M].Delft:Delft University Press,1982:33-46.
[11]Martinez-Saucedo G,Packer J A,Christopoulos C.Gusset plate connections to circular hollow section braces under inelastic cyclic loading[J].Journal of Structural Engineering,2008,135(7):1252-1258.
[12]Willibad S,Packer J A,Voth A P,et al.Throughplate joints to elliptical and circular hollow sections[C]//11th.International Symposium on Tubular Structures,Quebec,2006.
[13]Ariyoshi M,Makino Y,Choo Y S.Introduction to the database of gusset-plate to CHS tube joints[C]//Proceedings of 8th International Symposium on Tubular Structures,Singapore:Singapore Steel Construct,1998:22-28.
[14]Kim W B.A study on conections of circular hollow section with gusset plate[J].J Architectural Inst Korea 1997,13(3):263-271.
[15]Kim W B.A Study on the local deformation of tubular connection in truss[J].Conference Korean Society of Steel Construct,1995,7(2):135-140.
[16]Kim W B.Ultimate strength of tube-gusset plate connections considering eccentricity[J].Engineering Structures,2001,23(7):1418-1426.
(编辑 胡英奎)
Effects of Eccentricity on the Ultimate Strength of K-joint with Tube-gusset Plate Connections
WANGWeijia,LIUHongjun,LIZhengliang
(College of Civil Engineering,Chongqing University,Chongqing 400045,P.R.China)
The behavior and strength of tube-gusset connections with tube 219×6 and 1/4 annular ribbed plate subjected to eccentric force is investigated.Non-dimensionalized ultimate strength interaction relations between the wall moment of tube,vertical axial force,and eccentric vertical component force of axial brace force of tube-gusset connections with 1/4(1/2)and annular ribbed plate subjected to eccentric force is researched based on the model of equivalent forces of tubular joint.The parameters which influence the ultimate strength of tube-gusset joint were analyzed and non-dimensionalized ultimate strength interaction-relationships were proposed.It is shown that the proposal formula has theoretical and practical significance for design because of comparation with experimentation.
eccentricity;ultimate strength;tube-gusset connections;the model of equivalent force
TU312.1
A
1674-4764(2012)04-0091-07
2011-11-28
国家自然科学基金资助项目(51078367);中央高校基本科研业务费资助项目(CDJRC10200016)
王蔚佳(1959-),女,主要从事施工技术研究,(E-mail)cqdxwwj@163.com。
- 土木与环境工程学报的其它文章
- 高藻期超滤膜制水中试研究

