“资源三号”卫星三线阵影像几何质量分析

徐文 龙小祥 喻文勇 李庆鹏

（中国资源卫星应用中心，北京 100094）

1 引言

“资源三号”（ZY-3）卫星是我国首颗民用高分辨率光学传输型立体测图卫星，集立体测绘和资源调查功能于一体，主要用于1∶50 000立体测图及更大比例尺基础地理信息产品的生产和更新，开展国土资源调查与监测等。在卫星在轨测试期间，通过ZY-3卫星图像产品的内外部几何定位精度的评价与分析对其图像产品进行客观、真实的反映，将有利于用户更好的使用数据产品。

卫星图像数据的几何质量主要从如下两个方面来考察：1）外部几何定位精度，2）内部几何畸变。其中，外部几何定位精度是指图像几何定位坐标与真实坐标之间的误差，对无地面控制点的定位精度主要取决于：卫星影像获取时的星历数据和姿态数据的精度、载荷成像时刻计算精度、平台稳定性、传感器几何参数等。内部几何畸变是指图像内的若干固定点相对位置的距离与参考图像上同名点间相对距离的对比，反映图像的内部几何变形程度，通常包括图像内部的长度变形和角度变形，是评价高分辨率遥感影像几何精度的重要技术指标，用于反映光学成像系统的内部可靠性和遥感平台的稳定性。

由于地面测量相机视轴与卫星指向安装角误差以及星上姿态、轨道测量系统存在系统误差等因素，需要在地面处理中进行测量平差以剥离外方位系统误差与偶然误差。ZY-3卫星三线阵相机成像系统采用无畸变设计，但受卫星发射、环境变化以及在轨测试过程中焦面位置调整等因素的影响，需要在地面标定载荷的内方位元素。

本文主要研究分析ZY-3三线阵TLC影像的几何质量，并介绍地面数据处理系统三线阵影像的对地几何定位处理流程。

2 三线阵CCD影像成像模型

2.1 单线阵CCD影像成像模型

任何类型传感器的成像过程可通过一系列点的坐标转换来进行描述。通过一系列坐标系统建立推扫式卫星遥感影像的严格成像模型[1-2]。

1）相机坐标系与本体坐标系之间的旋转矩阵（即为相机安装矩阵）：

式中 r，p，y为本体坐标系与相机坐标系之间在X，Y，Z方向上的夹角。

2）本体坐标系与轨道坐标系间的旋转矩阵：

本体坐标系到当地轨道坐标系之间的旋转代表着卫星的姿态，根据两坐标系的空间位置容易得到

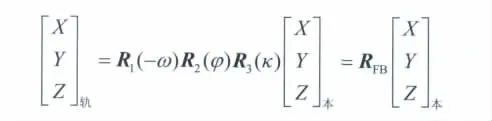
式中

式中 ω，φ，κ分别为卫星下传的姿轨数据中的滚动、俯仰、偏航角。

3）轨道坐标系与空间固定惯性参考系间的坐标变换

这两个坐标系统的变换主要是3个坐标轴的旋转以及它们原点的平移，通过变换可以建立地面系统与卫星系统之间的联系。

式中

4）地球固定地面参考系与空间固定惯性参考系间的严格坐标变换

式中 PN（t）为岁差和章动矩阵；R（t）为地球自转矩阵；W（t）为极移矩阵。

根据上述坐标转换关系，得到严格成像模型为[3]：

其中 （Xs，Ys，Zs）为摄站中心在 WGS84 下的坐标；（X，Y，Z）为物方点在 WGS84 下的坐标；（xi，yi，f）为相机坐标系下的坐标；m为比例系数。

2.2 三线阵TLC影像成像模型

三线阵CCD影像成像模型与单线阵CCD影像成像模型的不同之处就在于三线阵CCD影像前后视像点坐标中x值不为0。在三线阵CCD相机中因为3个线阵是平行排列的，所以在飞行方向上像点坐标是常数，若以x方向为飞行方向，即有：

其中f为相机的焦距；α为前视相机与正视相机和后视相机与正视相机的夹角，对于ZY-3卫星来说α为22°。

综上，列出三线阵CCD卫星影像的严格成像模型如下[4-5]：

前视

正视

后视

该严格成像模型忽略了投影中心与卫星质心的差距。其中，m为尺度因子；（x，y，-f）为像点在像空间坐标系下的瞬时坐标；（X，Y，Z）为地面点 k 在物方空间坐标系下的坐标，RGF、RFB、RBS与PN（t）、R（t））、W（t））分别为姿态旋转矩阵与偏置矩阵。

3 三线阵几何检校

卫星成像具有高轨道、窄视场角的特点，其成像过程中的各种系统误差之间互相耦合、紧密相关，若采用传统航空传感器的几何定标模型进行卫星的在轨几何定标，必然导致病态的解算方程，无法得到稳定高精度的定标结果。

对卫星成像过程中存在的各类系统误差进行分析发现，卫星在轨成像过程中存在的系统误差可以分为两大类：外部系统误差和内部系统误差。外部系统误差影响像点在传感器坐标系下的像点坐标，包括：相机安装角、时间同步误差、GPS偏心误差等；内部系统误差不影响像点在传感器坐标系下的坐标，仅影响其在CCD上的像素坐标，包括CCD在传感器焦平面上的平移、旋转、缩放、主距f的变化等线性畸变以及某些非线性畸变（如光学畸变）。定标模型可以对这些系统误差分别建模、解算，从而解决由于过度参数化导致解算方程的病态问题。

3.1 外方位元素求解方法

由于在立体摄影测量时，星上测量的外方位元素存在误差，如果全部带到严格成像模型中，会导致模型扭曲、影响几何定位精度，因此，需要通过空三区域网平差消除外方位元素引起的误差，提高遥感影像几何定位精度。

根据共线方程[6-7]：

式中 （x，y，f）为影像内方位元素；（Xp，Yp，Zp）为摄站的物方空间坐标；（Xg，Yg，Zg）为物方点的物方空间坐标；（ai，bi，ci）（i=1，2，3）为影像的 3 个外方位角元素组成的 9 个方向余弦。

将上式变形为：

对上述方程线性化处理，得到误差方程：

把误差方程式写成矩阵形式为：

考虑到地面点未知数比较多，定向片数有限，先求定向片外方位元素的未知数，然后再求地面点坐标未知数，利用最小二乘原理及消元法，将式V=Ax+By-L变形为：

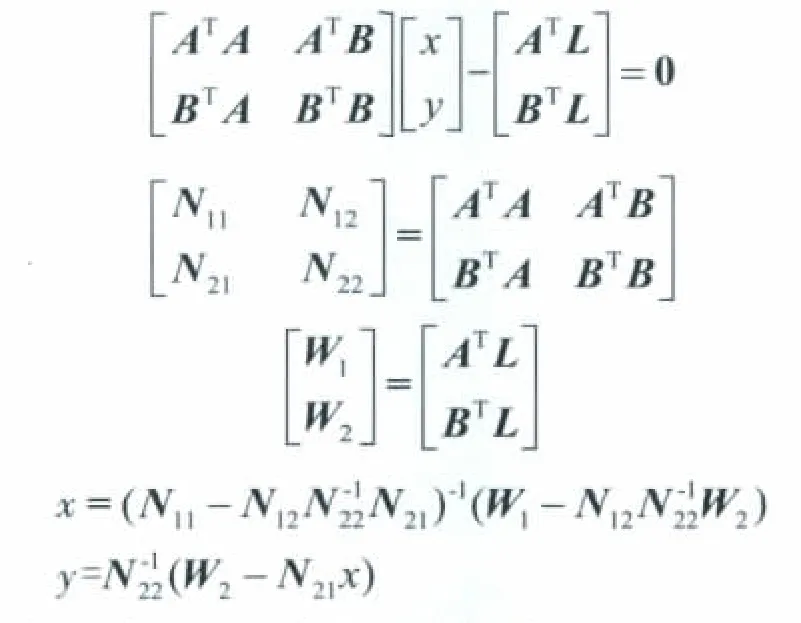
通过迭代求解定向片的外方位元素和地面点坐标未知数。

定向片法空三区域网平差的基本算法流程如下图1所示：

3.2 基于已知外方位参数的单相机内方位元素求解方法

3.2.1单相机内方位元素解算算法

利用控制点量测信息解算单相机外定标参数后，利用引入外定标参数的几何成像模型以及几何定标场高精度高程数据、正射影像生成模拟影像，通过将模拟影像与原始影像进行密集匹配，对同名像点间的残差分布进行分析，建立几何内定标模型，最后采用统计策略解算内定标参数[8-9]。

前述建立几何定标模型，若：

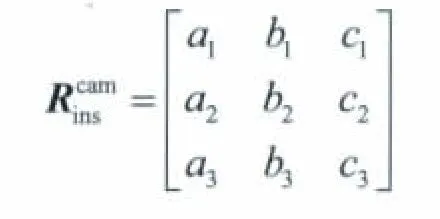
则：

将上式进行线性化处理，并列法方程得：

其中

利用不同时相、姿态角的影像，通过高精度影像匹配量测大量同名点，然后进行联合平差处理，解算定标参数。解算模型如下[10]：

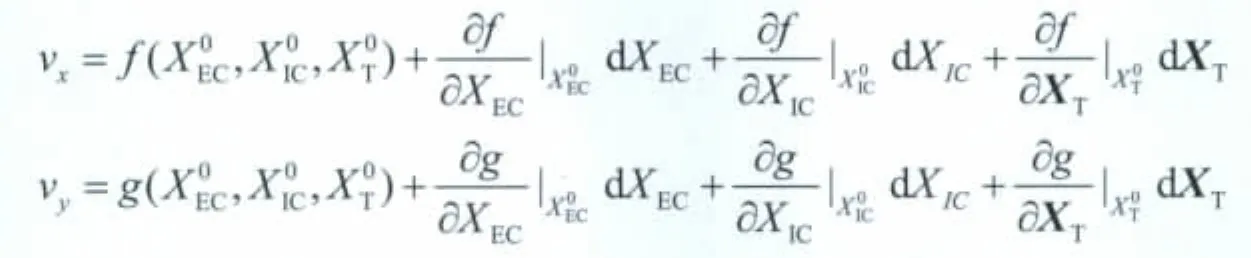
3.2.2单相机内定标参数解算策略

对待定标参数采用分步、分级迭代解求策略解算，包括以下内容：

1）对内外定标参数采取分步迭代求解。先假设内部定标参数初值为真值，即dXIC=0，解算外部定标参数改正数dXEC，然后假设外部定标参数改正数dXEC=0，解算内部定标参数改正数dXIC；迭代解算直至结果收敛。

2）通过几何分析、统计分析的手段，将待定标几何参数分级处理。把相关性强、可确定性低、影响因子小的参数设为低优先级；相反，把相关性弱、可确定性高、影响因子大的参数设为高优先级。不同优先级在平差解算中赋予不同的权重，并采用基于验后定权的广义最小二乘平差方法解算各待定标参数，提高解算精度和稳定性。

3）分析像方残差矢量与各定标参数的微分关系，针对不同定标参数，确定控制点布设方案，降低解算方程的相关性，提高解算精度。

4）利用同一扫描行不同探元之间的相对角度关系作为控制信息，消除外部系统误差的影响，解算内定标参数；利用连续扫描行上同一探元的残差分布特征作为解算信息，消除偶然误差的影响，解算内方位参数。

3.3 在轨几何检校处理流程

相机几何内定标参数解算主要包括：外定标参数解算、影像模拟、高精度同名像点匹配、内定标建模及内定标参数解算等步骤，几何检校流程如图2所示。

4 试验结果及分析

4.1 试验结果

卫星外方位元素与相机内方位元素的检校以嵩山几何定标场测量数据为高精度参考数据，计算卫星影像投影的偏置矩阵和相机每个探元的视向量。图3为视向量Y方向指向变化示意图，X方向无改变。

本试验1∶10 000高精度影像与SRTM90高程数据为参考基准，影像样本覆盖全国大部分地区，对ZY-3卫星下视产品的平面几何精度（计算测试图像与参考图像投影坐标差值）进行分析与评价。

直传姿轨数据定位产品的无控定位精度中误差的平均值在X方向为4.636个像素，在Y方向为3.514个像素，即在无地面控制点情况下，TLC影像几何定位精度在垂轨方向9.74m，沿轨方向7.38m，优于6个像元，见表1。

?

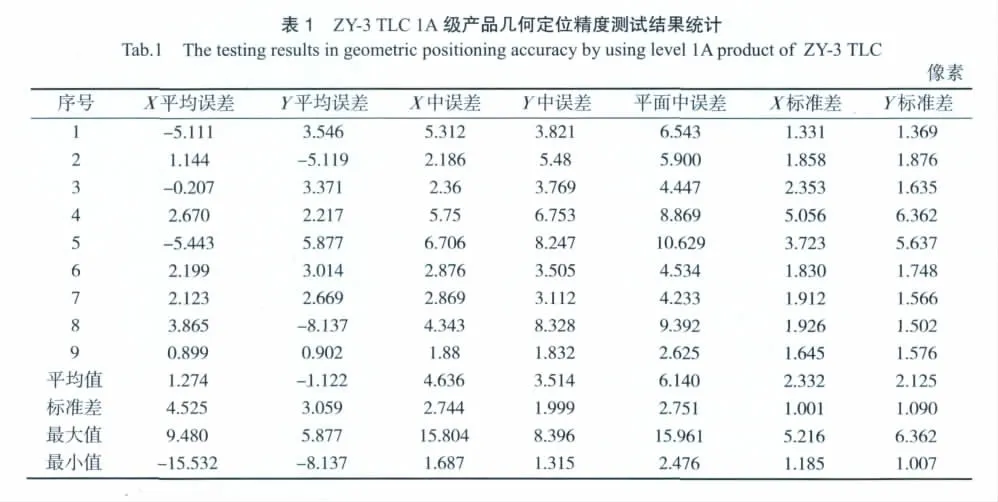
内部几何精度评价数据选取的是辽宁大连地区直传姿轨数据定位的正视全色Level 1A影像（成像时间为2012年1月11日），该区域既有平原、城市又有山地，数据代表性较好。选取分布均匀的控制点和检查点评价内部几何变形。ZY-3的正射影像几何变形中误差为3.47m，正射影像精度评价结果见表2。

?

4.2 结果分析

从图3中可以看出，三线阵相机的视向量在焦平面上的指向曲线对比实验室测量曲线呈线性向外扩张，而不是呈光学畸变中典型的“微笑”曲线，因此可以得出三线阵的光学系统实现了真正的无畸变设计，视向量沿线阵方向的扩张是由于焦平面上下移动导致。

卫星星敏测量精度设计为6"，卫星506km标准轨道高度下1"对应地面2.5m，定位误差为6×2.5=18m；GPS测量精度为5m。而影像的定位精度优于20m；与卫星的姿、轨测量精度符合。

卫星平台稳定性5×10-4（°）=1.8"，引起的几何变形为4.5m，而影像的几部几何精度优于1.5像元，与卫星平台的稳定性符合。

5 结束语

经地面系统检校计算出由于成像环境改变与焦面调整造成的内方位元素误差并分离卫星平台外方位元素的系统误差后，地面数据处理系统通过对ZY-3卫星三线阵影像的几何质量进行系统研究分析评价，结果表明ZY-3卫星三线阵相机影像无控制点的几何定位精度中误差达到13m（优于6个像元），内部几何变形优于2.97m（1.5像元），几何精度达到国际同类卫星先进水平，完全满足1∶50 000的测图要求。

卫星影像的无控制点几何定位精度与内部几何精度结果表明，相机光学系统与平台的稳定性表现优异，卫星平台的姿态、轨道、时间系统测量精度满足系统设计需求。

（References）

[1] 李德仁，郑肇葆.解析摄影测量[M].北京：测绘出版社，1992.LI Deren，ZHENG Zhaobao.Analytic Photogrammetry[M].Beijing：Surveying and Mapping Press，1992.（in Chinese）

[2] Zhang J，Zhang X.Strict Geometric Model Based on Affine Transformation for Remote Sensing Image with High Resolution[J].International Archives of Photogrammetry and Remote Sensing，2002，34（B3）：309-312.

[3] 张过.缺少控制点的高分辨率卫星遥感影像几何纠正[D].武汉：武汉大学博士论文，2005.ZHANG Guo.Rectification for High Resolution Remote Sensing Image Under Lack of Ground Control Points[D].Wuhan：Wuhan University Doctoral Dissertation，2005.（in Chinese）

[4] 宇超群.线阵CCD卫星遥感影像成像模型及算法研究[D].郑州：解放军信息工程大学硕士论文，2006.YU Chaoqun.A Study of the Imaging Geometry Models of Linear Array CCD Imagery of Remote-Sensing Satellites[D].Zhengzhou：PLA University Master Degree Thesis，2006.（in Chinese）

[5] Ebher H，Mueller F.Processing of Digital Three Line Imagery Using a Generalized Model for Combined Point Determination[J].Int.Arh.of Photogrammetry and Remote Sensing，1986，26（3）：203-208.

[6] 李德仁，赵双明，陆宇红，等.机载三线阵传感器影像区域网联合平差[J].测绘学报，2007，36（3）：245-250.LI Deren，ZHAO Shuangming，LU Yuhong，et al.Combined Block Adjustment for Airborne Three-line CCD Scanner Images[J].Acta Geodaeticaet Cartographica Sinica，2007，36（3）：245-250.（in Chinese）

[7] Ebher H，Mueller E H，ZHANG Senlin.Studies on Object Reconstruction from Space Using Three Line Scanning Imagery[C].In：Kyoto：ISPRS Com.Ⅲ，1988.

[8] 苏文博.航天线阵CCD传感器在轨几何定标技术研究[D].郑州：解放军信息工程大学硕士学位论文，2010.SU Wenbo.Research on Techniques for on-Orbit Geometric Calibration of Space Linear CCD Sensors[D].Zhengzhou：PLA University Master Degree Thesis，2010.（in Chinese）

[9] 汤志强，苏文博，葛海军.航天线阵CCD传感器内方位建模与优化[J].遥感信息，2010，45（6）：3-5.TANG Zhiqiang，SU Wenbo，GE Haijun.The Inner Orientation Modeling and Optimization of Space Line-array CCD Sensor[J].Remote Sensing Information，2010，45（6）：3-5.（in Chinese）

[10] Roger Y Tsai.A Versatile Camera Calibration Techniquie for High Accuracy 3D Machine Metrology Using Off-the-Shelf TV Camera and Lense[J].IEEE Journal of Robotic and Automation，2007，3（4）：323-342.