气囊着陆缓冲系统的冲击动力学多目标优化

何成陈国平何欢姜金辉

（1机械结构力学及控制国家重点实验室，南京 210016）（2南京航空航天大学振动工程研究所，南京 210016）

1 引言

探测器的着陆过程主要分为着陆下降减速和着陆接地缓冲两个阶段。在前一个阶段，大多是利用降落伞的气动阻力对登陆系统进行减速。然而，在实际工程中，降落伞降速能力的提高是以总质量和总体积为代价，因此受降落伞系统总质量和体积的限制，必须采取进一步的接地缓冲措施以确保登陆舱内携带的精密、贵重仪器设备等有效负载的安全。

缓冲气囊缓冲原理是利用系统着陆时，气囊内气体压缩来吸收着陆冲击能量，从而达到缓冲的目的。由于其良好的缓冲性能，并且具有质量轻，可折叠等特点，因此在汽车、航空、航天领域都得到了广泛应用[1,2]。近些年随着深空探测发展，大量精密探测器的着陆安全对缓冲系统的缓冲特性提出了更高的要求，因此如何合理设计缓冲系统，进一步提高其缓冲性能就显得尤为重要。

目前对气囊缓冲系统的冲击动力学研究方法主要分为试验分析方法和有限元仿真分析方法两类。由于试验方法最能直观反映出缓冲系统的真实特性，在国内外开展了大量研究工作[3-5]。但是受实际试验场地、试验技术水平、试验周期以及研究经费等条件限制，无法开展大量、大规模验证试验和研究。因此采用有限元仿真分析方法成为近些年进行气囊系统缓冲特性研究的热点，文献［6］以“火星探路者”着陆系统的全向式气囊缓冲装置为对象，利用有限元分析技术，实现气囊系统的建模与着陆全过程的仿真研究；文献［7］采用欧拉数值模型，研究了气囊初始内压、材料参数以及地面参数对着陆系统过载的影响。

虽然在气囊式着陆缓冲系统方面的研究论文较多，但在气囊系统着陆缓冲性能优化方面的研究开展相对较少。本文基于D最优试验设计建立的移动最小二乘（Moving Least Square，MLS）代理模型对类似于“猎兔犬”式气囊缓冲系统进行冲击动力学优化研究，将首次冲击最大过载、囊体织物最大应力作为优化目标，以囊内初始气压、绳刚度作为设计变量，引入理想点法完成了缓冲系统的多目标优化研究，并给出了多目标函数之间的Pareto前沿，为设计者使用封闭气囊作为缓冲系统提供参考依据。

2 代理模型的构造

2.1 D最优试验设计

由于实际试验需要考虑到研究周期以及试验成本等问题，因此在试验前进行合理的试验设计，可以在取尽可能少的试验样本点的情况下获得较好的试验效果，试验设计的任务就是为了解决这一问题。在构造全局近似函数时通常也借助试验设计来减少总的响应计算量。

D最优设计[8]作为一种试验设计方法在工程界得到了广泛应用，它是基于回归模型的一类试验设计方法，该方法对设计点的选择自由，在样本空间中无明显的分布规律。假设研究的回归模型为 ′，即

式中 x为设计空间中一点，设计空间为m维欧式空间；ε为服从方差为σ2的标准正态分布的测量噪声；fi（x）为形式已知的函数；a为回归模型系数。

将式（1）表示为矩阵形式

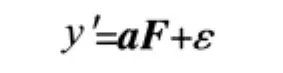
式中 F为模型的结构矩阵，通过最小二乘法可获得回归系数向量a的估计值。估计参数协方差矩阵为

通常定义信息矩阵M=FTF，D最优设计即为使得协方差矩阵取极小时所对应的设计点集，或等价于使得信息矩阵的行列式取极大。

2.2 移动最小二乘法基本格式

MLS法最早是无网格法（SPH）逼近函数的方法之一，是无网格伽辽金法的核心。随着学科间的交叉与渗透，MLS法在图形处理和数据拟合等领域都获得了较广泛的研究与应用[9]。近些年，在工程界逐渐将MLS法应用于代理模型构建中[10]，并很快形成了一种新的代理模型构造方法。另外由于MLS法采用回归近似技术并且系数具有可变性，从而使得它不仅对工程问题中的数值噪声有很好的过滤作用而且在拟合高度非线性模型时具有良好的精度。

假定真实响应函数为 ，由MSL法回归得到的近似值为 ′，MLS法将待求函数表示为一系列基函数的线性叠加形式，即

式中 a=[a1（x），a2（x），…，am（x）]T为待定系数，它是 l维设计参数向量 x=｛x1，x2，…，xl｝的函数。p=[p1（x），p2（x），…，pm（x）]T为基函数，它是一个完备多项式，m为基函数项数。二维空间中单项式基函数为

为度量代理模型对目标函数的逼近程度，定义逼近函数残差的离散加权L2范数J为：

生态环境遭受人为的严重破坏，生态环境日益恶化，自然森林植被、灌木、树少林稀，极大地削弱了植被涵养水源、保持水源、调节气候、减少蒸发的作用，致使本区地表、地下水资源短缺，地表河流及山间溪沟水流量逐年减少。该区内许多岩溶泉水正因为周边生态环境遭受破坏，导致流量逐年减少，甚至枯竭断流。此外，由于生态环境的破坏，每逢丰水雨季径流量大还造成水土流失，直接淤积江河及岩溶地下空间，从而引发严重的洪涝灾害。

式中i=‖x-xi‖／r，（r是影响半径）；n是影响区域内设计样本点的个数；i是 xi处样本点处响应值，w（i）是样本点xi的权函数，常用的有3次样条权函数与高斯权函数，在本文中采用工程中常用的高斯权函数：

将式（2）写成矩阵形式：

式中

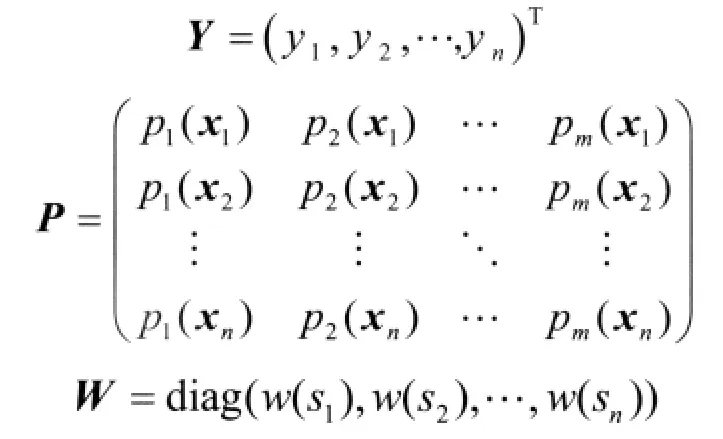
由最小二乘法求得系数

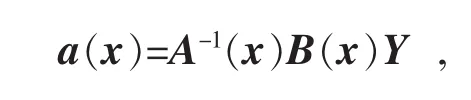
式中

移动最小二乘法可以通过取不同阶的基函数获得不同的拟合精度，取不同的权函数以改变拟合曲面光滑度，这是其他拟合方法无法比拟的。需要注意的是，A矩阵可逆影响半径必须满足一定的条件：p（x）为二维线性基时，影响半径内至少包含3个不共线的样本点；p（x）为二维二次基时，影响半径内至少6个样本点，且这些点不在任何1条二次曲线上。

2.3 模型误差评价准则

ANOVA统计分析技术不仅可以作为评价响应面模型适合性的一种方法，并且能够对设计变量的影响水平进行评价。本文选取常用与评价模型适合性的统计学判定系数R2与均方误差根（RMSE）作为代理模型精度的评价参数。其中

式中 N为总的样本点个数；i与i′是样本点空间中各点的响应真值和代理模型计算值；是样本点空间中各点响应真值的均值。RMSE的大小表示代理模型误差值所占真实平均值的百分比；R2判定系数代理模型与真值之间的总体差异程度，取值范围为0～1之间，一般来说，R2值越大，RMSE值越小，模型的合适性就越高。

3 封闭式气囊系统的着陆缓冲性能多目标优化

3.1 有限元模型及其优化问题描述

本文以类似于“猎兔犬”缓冲登陆系统为对象，以真实火星环境为输入条件，对该系统进行缓冲性能优化。有限元模型如图1所示，该登陆系统由气囊织物、登陆舱以及收缩绳3部分组成。收缩绳采用MSCDytran所支持的“安全带”一维单元进行模拟，并假设绳索的力与应变呈线性关系。初始模型织物参数为，密度875kg/m3，弹性模量6.43GPa，泊松比0.3，阻尼系数0.1，收缩绳刚度为1.5×104N。

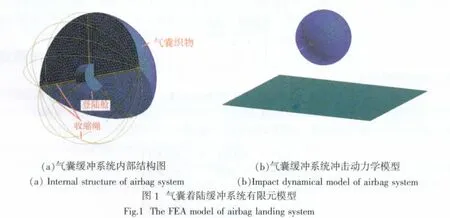
着陆缓冲系统以60°的入射角，着陆速度为18m/s进行着陆，接触分析中采用的静摩擦系数和动摩擦系数均取0.3。由于目前尚缺乏一些真实参数的数据支持，本文所取的分析参数有可能与真实情况不符，但并不妨碍所研究方法的普遍性。由于在整个着陆缓冲过程中，首次着陆冲击过载远远大于后续弹跳过程中产生的冲击过载，因此只以首次着陆的一个完整冲击过载的峰值作为优化目标。另外，在着陆冲击过程中，气囊织物承受较大的面内张力，对系统进行合理的设计可以防止气囊因冲击载荷作用而产生爆破，因此对气囊织物承受的最大应力也需要进行优化控制。

本文选取初始气压Pr与收缩绳刚度k（每单位应变所需要的力）作为设计变量，以初始模型参数作为优化空间中心，将设计变量Pr、k设计范围分别设定为[3 000,6 000]Pa，[0,3]×104N，则优化问题可描述为

式中f1为最大过载；f2为气囊织物最大应力；Φ为多目标优化的目标函数。

3.2 样本点的确定及其对应的响应

采用D最优试验设计方法，选取样本点数目为22个。通过样本点对应的样本值，采用非线性瞬态有限元分析程序MSC.Dytran作为核心求解器，计算得到在样本点处的最大过载与最大应力。由于计算得到的加速度信号中含有大量的高频成分，掩盖了对登陆舱设备过载起决定作用的低频脉冲，故采用文献[11]的方法对过载信号进行滤波，本文选取的滤波截止频率为60Hz。表1给出了样本点的空间位置及其对应的目标函数值。

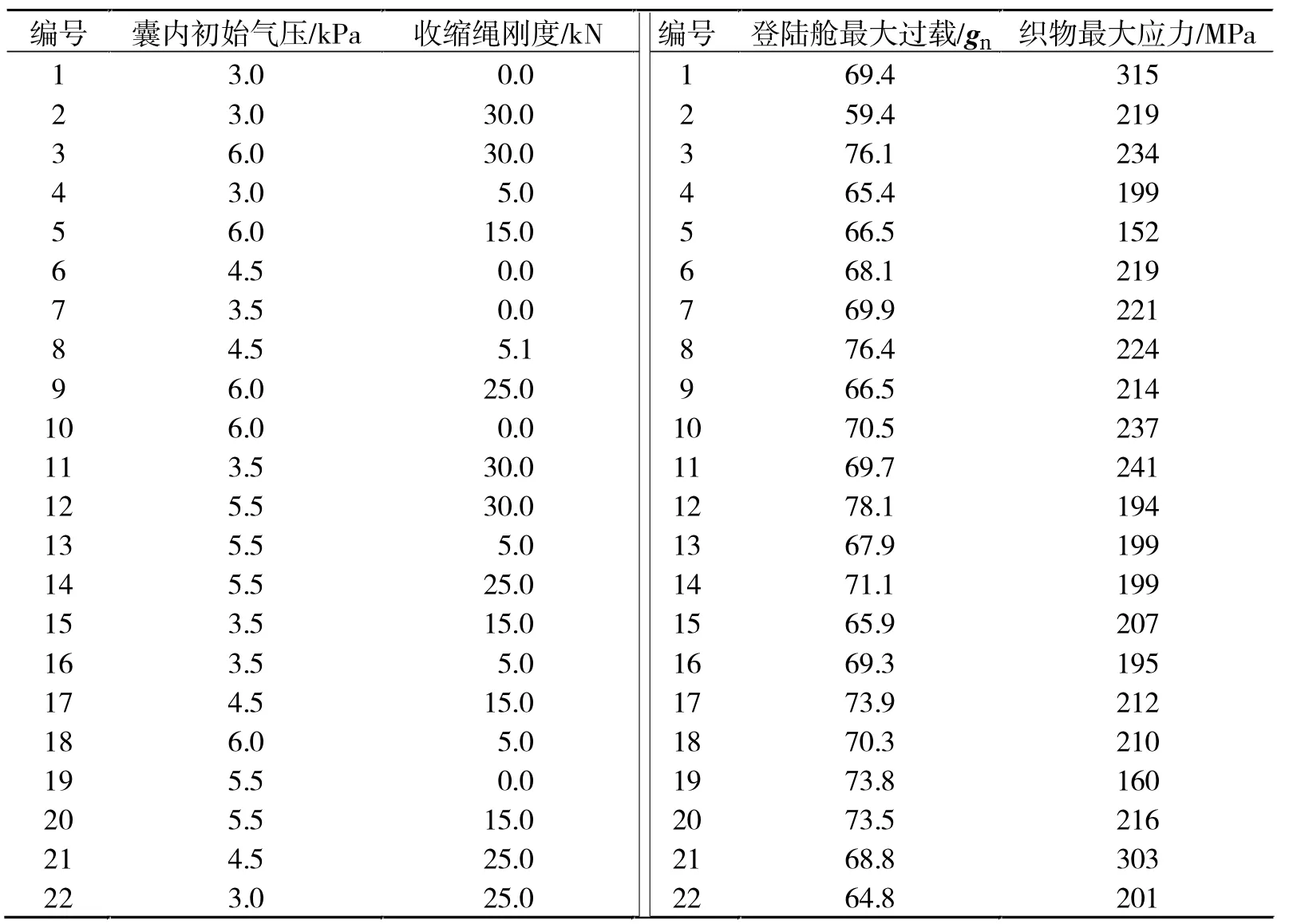
表1 样本点及对应的目标函数值Tab.1 Design matrix and values of objective functions

3.3 优化分析

利用MSL构造设计变量与各个目标函数之间的映射关系，其对应的响应面如图2、3所示。对每个目标函数的代理模型适合性进行评价，计算发现：最大过载的响应面RMSE值仅为0.001 8，判定系数R2最小值为0.980 7，最大应力的响应面RMSE值仅为0.006 3，判定系数R2最小值为0.967 2，可见每个模型完全满足精度要求，可以进行后续优化工作。

从图2、3中可以看到，在设计空间内最大过载极大值为78.2gn，而最大过载极大值与极小值之间相差18.5gn，接近极大值的24%。同样的最大应力极大值为310MPa,极大值与极小值之间相差154MPa，占到极大值的49%，可见各个目标函数都具有较大的可优化空间；设计变量对目标函数的影响程度有差别，目标函数对收缩绳刚度的变化更为敏感，而随初始气压的变化相对平缓；系统的最大过载随囊内部初始气压和收缩绳刚度增大而增大，在低压力区收缩绳刚度影响较为复杂；总体而言最大应力呈现出随收缩绳刚度增加而增大的趋势，但是在设计空间的顶点处最大应力有不同程度的升高。

引入理想点法，通过构造统一目标函数使多目标问题转化为单目标优化问题进行优化。令各分目标的理想最优值为（i=1，2），定义

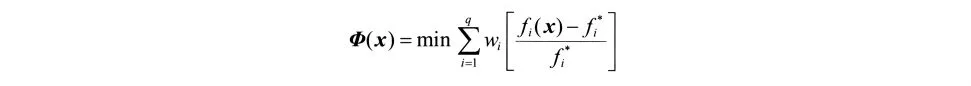
式中 q为目标函数个数；wi是第i个目标函数所对应的加权因子，文中采用归一权处理。由于响应面表现出的非线性程度不同，特别是针对响应面是多峰函数的情况，因此采用全局寻优能力较强的遗传算法进行寻优。

通过变化不同的权系数可以得到侧重不同目标分量的Pareto解集。解集是一个全局的相对最优解，设计者可以在解集中根据不同的优化要求与侧重点进行选取。本文采用Monte-Carlo模拟结合MSL代理模型，计算获得了目标函数的Pareto前沿，如图4和图5所示。为便于区分，在图中进行了编号处理。

图4 缓冲系统设计参数Pareto前沿Fig.4 The Pareto front of design parameters

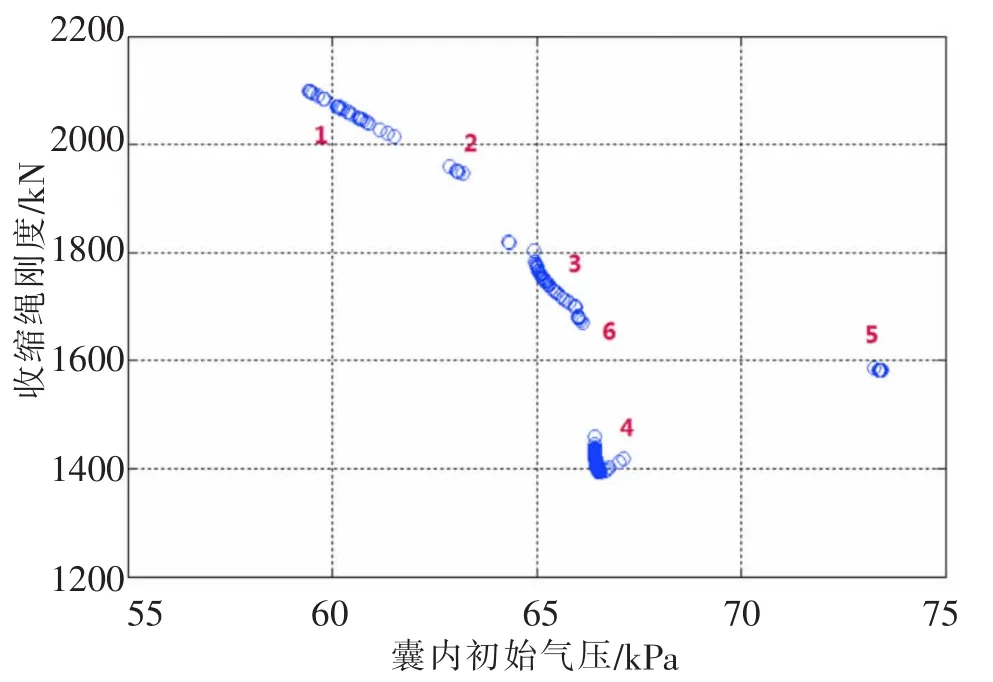
图5 缓冲系统优化目标的Pareto前沿Fig.5 The Pareto front of objective functions

从图中可以看出：1）Pareto解集多集中于特定域内，且多分布于设计空间的边界，呈现出聚类分布特征。2）在设计空间顶点“1”区域，可以获得设计域内最大过载的极小值，若决策者更加注重对登陆舱过载的控制，可以选择该区域内的设计点。3）当初始气压处于3 000Pa附近的低压力区时（对应图4与图5中“1”-“3”区域），收缩绳的刚度是对目标函数起主要作用的因素，最大过载与最大应力表现出相反的变化趋势，即织物最大应力随着首次最大过载的增大而减小。4）当系统初始气压在高压力区时（对应图4与图5中“4”区域），可以得到设计域内织物最大应力的全局最优值。若决策者较为关注气囊织物强度，可以选择该区域内的设计点。

分别从“1”和“4”区域内选出优化解分别定义为“优化系统1”与“优化系统2”，图6和图7分别给出了优化后系统的变形和首次冲击过载的时域曲线。图7结合表2可以看出优化系统不仅最大程度的优化了重点关注的单个目标函数，而且其他优化目标性能也获得了不同程度的提高，采用此种优化方法达到了预期效果。

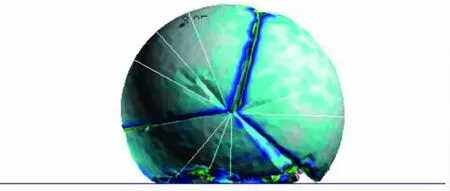
图6 优化系统2的应力与变形图Fig.6 The stress of second landing system after optimization

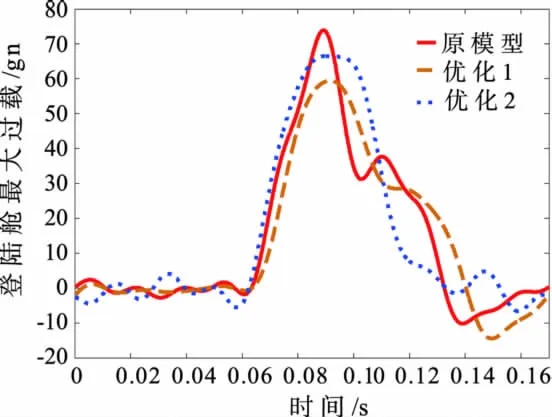
图7 优化前后系统冲击过载时域曲线Fig.7 Time history of overloading before and after optimization

表2 优化前后系统缓冲性能比较Tab.2 Cushioning performance of landing system before and after optimization

4 结束语

本文研究了基于D最优试验设计结合MLS法的气囊着陆缓冲动力学多目标优化问题。优化结果表明，利用MSL构造的代理模型能够非常好的逼近强冲击载荷下的冲击响应响应面，在此基础上进行优化分析能够给出合理的优化分析结果。

文章针对气囊着陆缓冲系统的囊内部初始气压和收缩绳刚度进行了优化分析，有效的降低了气囊着陆冲击最大过载和织物上承受的最大应力，证明了所提出的优化设计方法的有效性。研究结果还表明，收缩绳的引入使得初始气压对目标函数影响规律更加复杂，最大过载和最大应力呈现出较高的非线性特征。总体而言最大过载表现为随囊内部初始气压和收缩绳刚度增大而增大的趋势，最大应力随收缩绳刚度增大而增大，且收缩绳刚度对最大过载和织物最大应力的影响更加显著。

（References）

[1] 戈嗣诚.火星全向气囊的着陆缓冲特性研究[J].航天返回与遥感,2012,33(2)∶16-22.GE Sicheng.Study on Cushioning Characteristic of Mars Omni-direction Airbag[J].Spacecraft Recovery and Remote Sensing,2012,33(2)∶16-22.(in Chinese)

[2] 万志敏,谢志民.气囊缓冲飞行器模型着陆特性的试验研究[J].试验技术与试验机,2003,43(1)∶9-12.WANG Zhimin,XIE Zhiming.Study on Cushioning Characteristic of Airbag Landing System by Experiment[J].Test Technology and Testing Machine,2003,43(1)∶9-12.(in Chinese)

[3] Gardinier D J,Taylor A P,.Design and Testing of the K-1 Reusable Launch Vehicle Landing System Airbag[R].AIAA,1999,1757∶1-10.

[4] Cadogan D,Sandy C,Grahne M.Development and Evaluation of the Mars Pathfinder Inflatable Airbag Landing System[J].Acta Astronautica,2002，50(10)∶633-640.

[5]DaveN,Chris M.Improved Inflatable Landing Systems for Low Cost Planetary Landers[J].Acta Astronautica,2006，59∶726-733.

[6] 邓春燕,裴锦华.全向式气囊着陆装置缓冲过程的仿真研究[J].中国空间科学技术,2010,30(1)∶78-83.DENG Chunyan,PEI Jinhua.Simulation about Buffer Process of Omni-directional-type Airbag Landing Device[J].Chinese Space Science and Technology,2010,30(1)∶78-83.(in Chinese)

[7] 戴华杰,胡振东,咸奎成，等.火星探测器气囊缓冲系统着陆过程仿真[J].力学季刊,2010,31(4)∶555-561.DAI Huajie,HU Zhendong,XIAN Kuicheng,et al.Simulation Analysis for Landing Process of A Mars Detector with Airbag Buffer System[J].Chinese Quarterly of Mechanics， 2010,31(4)∶555-561.(in Chinese)

[8] Bu S L,Wang S Q,Ye H Q.An Algorithm Based on Variable Feedback to Synchronize Chaotic Systems[J].Physica D,2002,164∶45-52.

[9] 邵卫云,张雄.水泵水轮机全特性曲线的拟合-移动最小二乘近似[J].水力发电学报.2004,23(5)∶102-106.SHAO Weiyun,ZHANG Xiong.A New Simulation Method of Complete Characteristic Curves of Reversible Pump Turbine-moving Least Square Approximation[J].Journal of Hydroelectric Engineering.2004,23(5)∶102-106.(in Chinese)

[10] 张勇.基于近似模型的汽车轻量化优化设计方法[D].湖南大学,2008.ZHANG Yong.Optimization Design Method of Vehicle Lightweight Based on Approximate Model[D].Hunan University,2008.(in Chinese)

[11] Burrow L T.Verification Testing of a UH-1 Wire Strike Protection System(WSPS)[M].S Army Applied Technology Laboratory(AVRDCOM),1982.