满足裂缝宽度限值条件下纵向受拉钢筋的配筋量分析

张晓燕，刘许超

（1．华北水利水电学院，河南 郑州 450011;2．黄河勘测规划设计有限公司，河南郑州 450003）

钢筋混凝土构件除了可能由于强度不足而使结构失效外，还可能由于变形过大或裂缝宽度过宽，使结构不能正常使用．因此，设计中除了要进行承载能力极限状态配筋计算，还需要根据使用要求对构件进行裂缝宽度和变形计算，满足变形或裂缝宽度限制的控制．

在水工结构设计中，根据以往实际工程经验，当混凝土保护层厚度较大时，运用SL/T 191—96规范会出现钢筋用量由裂缝宽度限制条件控制，比承载力所需钢筋用量增加很多的情况．考虑到混凝土保护层较大时，表面裂缝虽有所增加，但耐久性有所改善，此时裂缝计算宽度的保证率可以略微降低．因此新规范SL/T 191—2008对裂缝宽度公式做了适当的调整，降低了混凝土保护层厚度对裂缝宽度的影响．在满足裂缝宽度限值的条件下，按照新、旧规范计算所需的纵向受拉钢筋的配筋量也发生了变化，笔者针对这一问题进行了研究，以期作为工程设计的参考．

1 新、旧规范裂缝宽度验算公式

1．1 裂缝宽度限值wlim

裂缝宽度限值是根据结构的功能要求、环境条件对钢筋的腐蚀影响、钢筋种类对腐蚀的敏感性以及荷载作用时间等因素来考虑的．然而到目前为止，一些同类规范考虑裂缝宽度限值的影响因素各有侧重，具体规定并不完全一致．“2008规范”参考国内外有关资料，根据钢筋混凝土结构构件所处的环境类别，规定了相应的最大裂缝宽度限值wlim．环境类别由“96规范”的4类变为5类，最大裂缝宽度限值也相应做了细微调整，但两者总体上是相当的．

1．2 最大裂缝宽度wmax计算公式

“2008规范”规定，配置带肋钢筋的矩形、T形及工形截面受拉、受弯和偏心受压钢筋混凝土构件，在荷载效应标准组合下的最大裂缝宽度wmax可按下式计算［1］

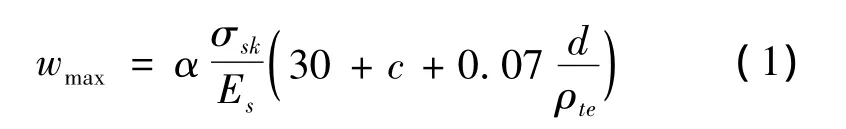
式中：α为考虑构件受力特征和荷载长期作用的综合影响系数，对于受弯构件，α=2．1，对于偏心受压构件，α =2．4，对于轴心受拉构件，α =2．7;c为最外层纵向受拉钢筋外边缘至受拉区边缘的距离，mm;d为钢筋直径，mm;ρte为纵向受拉钢筋的有效配筋率，ρte=As/Ate，当 ρte＜0．03 时，ρte=0．03;Ate为有效受拉混凝土截面面积，mm2，对受弯、偏心受拉及大偏心受压构件，Ate=2ab，a为受拉钢筋重心至截面受拉边缘的距离，mm;b为矩形截面的宽度，mm;As为受拉区纵向钢筋截面面积，mm2，对受弯、偏心受拉及大偏心受压构件，As取受拉区纵向钢筋截面面积，对全截面受拉的偏心受拉构件，As取拉应力较大一侧的钢筋截面面积，对轴心受拉构件，As取全部纵向钢筋截面面积;σsk为按荷载标准值计算的构件纵向受拉钢筋应力，N/mm2;Es为钢筋弹性模量．

与“96规范”相比，该公式有改动，具体如下．

1）将“96规范”公式中的构件受力特征系数α1、钢筋表面形状系数α2和荷载长期作用影响系数α3简化整合成综合影响系数α．

构件受力特征系数α1取值与“96规范”相同，对受弯和偏心受压构件，α1=1．0;对于偏心受拉构件，α1=1．15;对轴心受拉构件，α1=1.3．

对于有限裂要求的钢筋混凝土构件，应配置带肋钢筋，因此钢筋表面形状系数α2=1．0．

“96规范”中，正常使用极限状态验算的荷载效应组合是按短期、长期两种荷载效应组合进行的，由于对长期组合中的可变荷载标准值长期组合系数ρ的具体取值未明确给出，计算难以操作．“2008规范”取消了“荷载效应长期组合”，将抗裂、裂缝宽度验算及变形验算等正常使用极限状态验算的荷载效应组合均改为只按荷载效应标准组合（即原先的短期组合）计算，使计算简化．荷载长期作用影响系数α3只考虑荷载效应标准组合，取为1．5．

2）适当降低了保护层厚度对裂缝宽度的影响程度．

3）考虑到钢筋表面形状对裂缝宽度的影响，结合了我国钢材生产现状和发展趋势，“2008规范”明确规定，需控制裂缝宽度的配筋不应选用光面钢筋，如因某些特殊原因选用了光面钢筋，其最大裂缝宽度可能比“2008规范”公式计算值增大40%．

4）在“2008规范”中，最大裂缝宽度验算按荷载效应标准组合进行．荷载效应标准组合是指永久荷载和所有可变荷载同时采用其标准值的组合．有时某些可变荷载的标准值在总效应组合中占的比重很大但只在短时间内存在．例如作用在水电站厂房吊车梁上的轮压标准值（最大起重量），只在水轮发电机组安装或大修时才会出现．在这种荷载组合作用下，裂缝开展宽度的最大值只在短暂时间内发生，并且卸载后裂缝可部分闭合，对结构的耐久性并不会产生严重影响．因此，“2008规范”规定，凡此类按不常出现的荷载标准值计算的各种结构构件，均可将计算得出的最大裂缝宽度乘以一个小于1的系数．

2 满足wlim条件下所需的纵向钢筋配筋量 As，min

以受弯构件为例，Ⅱ级安全级别，处于露天环境，纵向钢筋选择HRB335级．

2．1 应用“2008规范”求解

2．2 应用“96规范”求解

“96规范”规定，对于矩形、T形及工形截面的钢筋混凝土受拉、受弯和偏心受压构件，按荷载效应的短期组合（并考虑部分荷载的长期作用影响）的最大裂缝宽度wmax可按下式计算［3］．

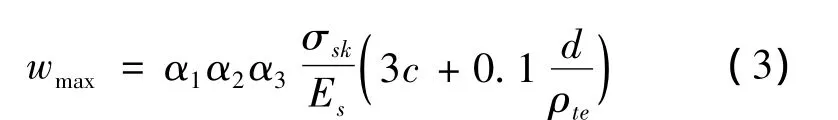
式中各符号意义同前．

取整简化后，公式（3）转化为

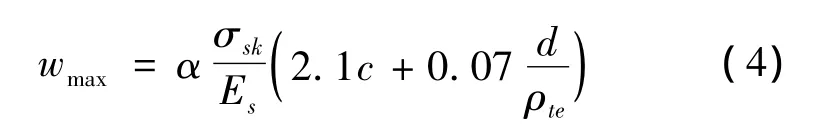
将公式（4）与公式（1）比较，可以看出两个公式最大的区别是混凝土保护层厚度对最大裂缝宽度的影响不同．

由公式（4）也可得到满足限裂条件的As，min的一元二次方程式，方程解与“2008规范”相比，系数B值不同，系数A，C相同．即

3 算例分析

某钢筋混凝土矩形截面简支梁，Ⅱ级安全级别，处于露天环境，截面尺寸250 mm×600 mm，计算跨度l0=7．20 m;混凝土强度等级C25，纵向受力钢筋采用HRB335，使用期间承受均布荷载，荷载标准值为：永久荷载标准值gk=13．0 kN/m（包括自重），可变荷载标准值qk=7．2 kN/m．

按照“2008规范”和“96规范”进行正截面承载力计算，该简支梁在标准荷载作用下产生的跨中弯矩Mk=130．9 kN·m．二类环境（室内潮湿环境，露天环境，长期处于水下或地下的环境）条件下wlim=0．3 mm ．

3．1 c 和 d 对 As，min的影响规律

根据公式（2）和公式（5），变换混凝土保护层厚度c从35 mm至60 mm，变换纵向受拉钢筋直径d从12 mm至28 mm，运用“2008规范”和“96规范”求解满足wlim条件下所需的纵向钢筋配筋量As，min，如图1所示．

由图1可知：按照“2008规范”计算，当钢筋直径不变，在满足wlim条件下，所需的纵向受拉钢筋的配筋量As，min随着混凝土保护层厚度c的增加基本上呈线性增加，保护层厚度c平均每增加5 mm，所需最小配筋量平均增加6．4%左右;而按照“96规范”计算，保护层厚度c平均增加5 mm，所需最小配筋量平均增加10%左右．由此可见，“2008规范”降低了混凝土保护层厚度对裂缝宽度的影响．按照“2008规范”计算，当混凝土保护层厚度不变，在满足wlim条件下，所需要的纵向受拉钢筋的最小配筋量As，min随着钢筋直径的增加而增加，且钢筋直径每增加一个级别，所需最小配筋量平均增加3．5%;而按照“96规范”计算，随着钢筋直径每提高一个级别，所需要的纵筋最小配筋量平均增加2．8%．

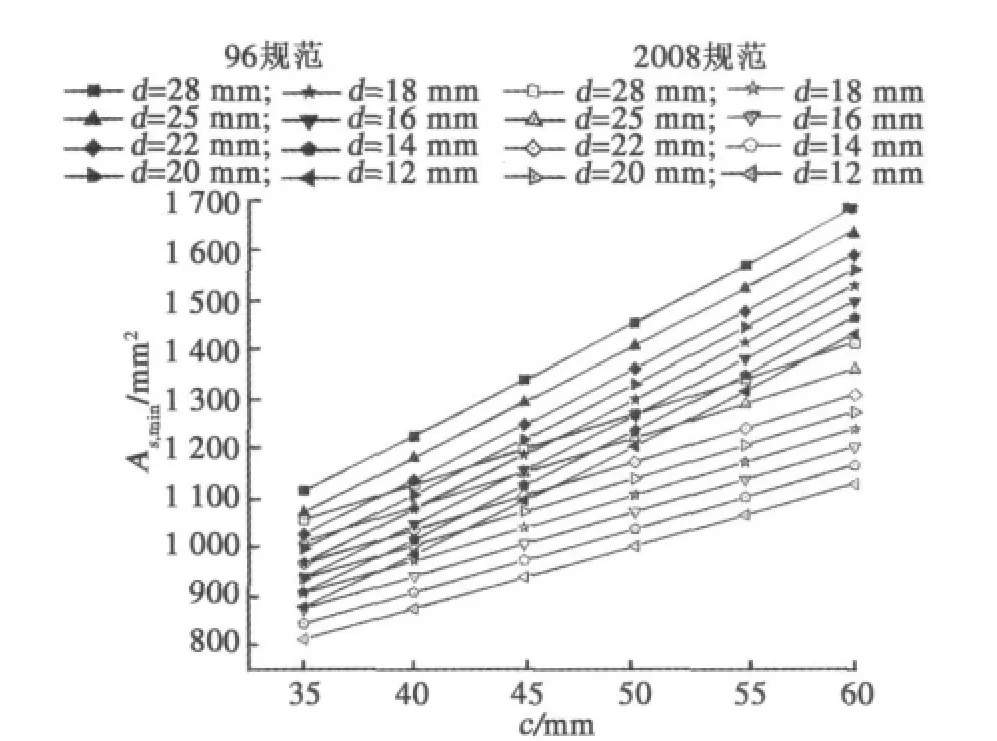
图1 c和 d对 As，min的影响规律

3．2 “2008 规范”较“96 规范”As，min的减少率

在构件尺寸、材料、荷载均相同的条件下，计算分析在满足wlim条件下“2008规范”较“96规范”As，min的减少率，结果见表 1．

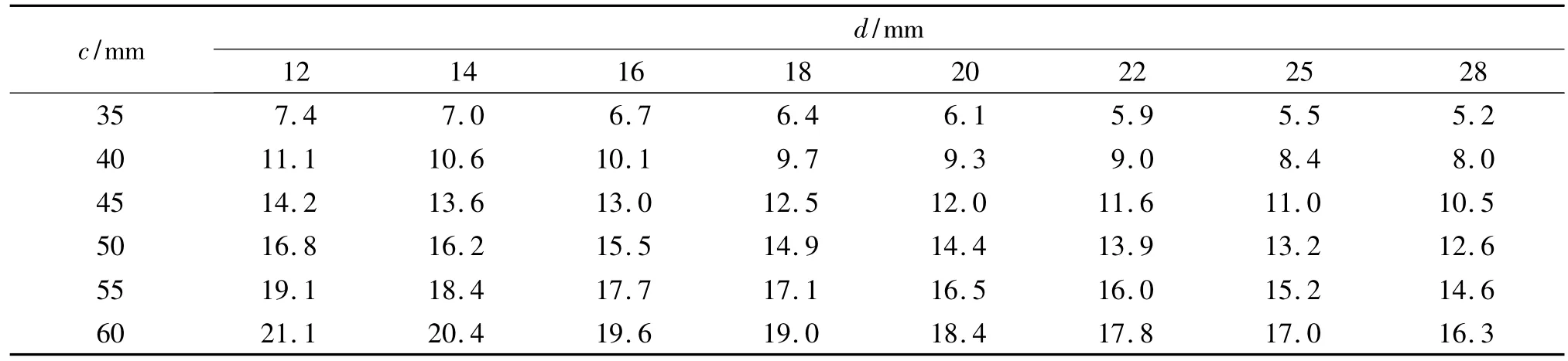
表1 “2008规范”较“96规范”所需的As，min的减少率 %

由表1可以看出，其他条件不变，“2008规范”比“96规范”满足wlim所需的纵筋最小配筋量As，min有所减少．随着混凝土保护层厚度的增加，As，min的减少率逐渐增大;随着直径的增大，As，min的减少率逐渐减小．对于大厚度的混凝土保护层，“2008规范”比“96规范”计算的纵筋最小配筋量As，min的减少率较大，如60 mm的混凝土保护层厚度，采用直径为12 mm的钢筋，满足wlim的纵筋最小配筋量As，min用“2008规范”计算的结果比“96规范”减少21%．

4 结语

满足裂缝宽度限值的条件下，运用“2008规范”计算所需的纵向钢筋的配筋量比“96规范”少，从而缓解裂缝宽度限值控制钢筋配筋量的工程情况．由此可见，“2008规范”规定的裂缝宽度公式更符合实际工程需要．

［1］水利部长江水利委员会长江勘测规划设计研究院．SL/T 191—2008水工钢筋混凝土结构设计规范［S］．北京：中国水利水电出版社，2008．

［2］河海大学，武汉大学，大连理工大学，等．水工钢筋混凝土结构学［M］．4版．北京：中国水利水电出版社，2011．

［3］水利部长江水利委员会长江勘测规划设计研究院．SL/T 191—1996水工钢筋混凝土结构设计规范［S］．北京：中国水利水电出版社，1996．