基于G M(1,1)模型和模拟退火算法的中长期负荷预测
张 军 ,尹 昊 ,缪思怡
(1.湖南省宁乡县供电局,湖南 宁乡 410600;
2.湖南大学,湖南 长沙 410082;3.三一重工,湖南 长沙 410100)
中长期负荷预测在电力系统规划和运行方面发挥着重要作用,具有明显的经济效益,负荷预测实质上是对电力市场需求的预测。灰色预测具有要求样本少、运算简便和精度高的优点,得到了广泛的应用。由于GM(1,1)的预测精度依赖于模型参数的准确度,使其难以达到理想的预测效果。针对上述情况,本文提出模拟退火 SA算法优化 GM(1,1)的方法,该方法能自动优化 GM(1,1)的参数,寻找全局最优解,有效地提高了GM(1,1)的预测精度。在中长期负荷预测中取得较好的效果。
1 GM(1,1)预测模型原理
GM(1,1)表示 1个变量、一阶方程预测模型,假设样本x0=(x01,x02,…x0n),建模步骤如下:
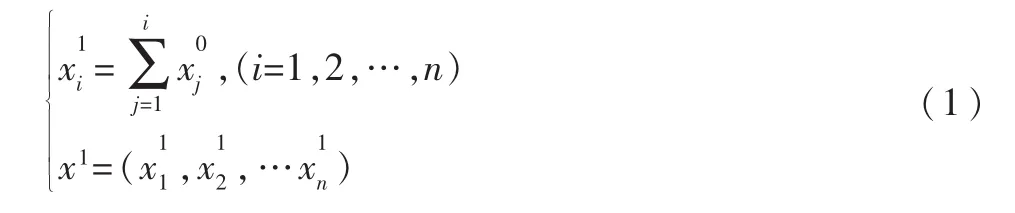

(1)对样本序列 x0做一阶累加生成 x1:模型中参数[a b]估计的好坏直接影响到预测的结果,而最小二乘法是基于残差平方和最小寻优,容易陷入局部最小,对于非线性较强的负荷,会产生很大的偏差[1]。另一面最小二乘稳健性较差,若中长期负荷存在奇异点,应用最小二乘法会导致异常数据产生过分不恰当的影响,从而影响到 GM(1,1)模型的预测精度,因此,引入模拟退火算法来实现参数的自动优化。
2 模拟退火算法
模拟退火算法是模拟无序热动力系统退火冷却过程的行为,将统计学应用到热力学的理论中[2]。将固体加热,此时固体内部粒子因高温而变得无序,伴随温度参数的不断下降,固体内部例子慢慢趋于有序,内能减少,当系统能力处在最低平衡态时得到最优解。根据设定模型在各参数的设定范围内随机产生一个初始解x(k)在此初始解邻域内产生一新解 x(k+1);根据目标函数计算 增 量 △E=E(xk+1)-E(xk);如 果 △E<0 则 xk+1被接受,否则根据boltzmann概率p和随机产生的概率阈值r(r∈[0,1])进行判断,如果 p>r,则 xk+1被接受,否则被拒绝。对当前解重复“产生新解->计算目标函数差->接受或拒绝”,并逐步降温,最后得到的当前解趋于全局最优解。其中boltzmann概率T表示温度。
SA算法是伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即全局最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法,理论上算法具有概率的全局最优化性能。
3 混合模拟退火算法与GM(1,1)方法结合
结合模拟退火算法的优化方法和 GM(1,1)的预测方法,本文给出混合模拟退火算法与 GM(1,1)相结合的负荷预测方法,即模拟退火 GM(1,1)模型:

(4)参数初始化
设定参数范围 a∈[-1,1],b∈[0.600],设定初始温度T0(T0>0)、目标函数精度 ε=0.01和基本步长 S0。 随机生成初始解 C0,检验抽样稳定的阈值为 N,退火为时间t。设定目标函数为:

其中 c为随机产生的 a、b值。 计算目标值 E (C0),令Eopt=E(C0),Copt=C0。
(5)利用模拟退火算法确定 GM(1,1)的参数
如果没有达到检验精度,设定Ci+1=Ci+γS0作为领域函数生成新解,γ是服从柯西分布的随机扰动,S0为与初始值及取值范围有关的步长值。计算新的目标值E(Ci+1)并按照模拟退火算法步骤(6)中给出的方法决定当前解Ci+1的取值。
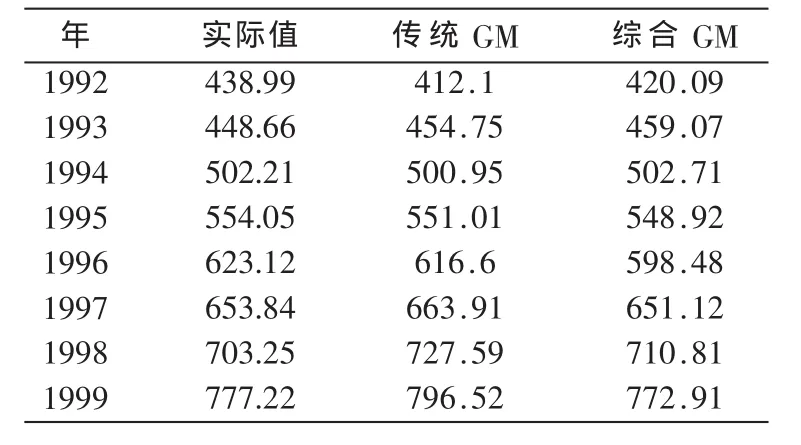
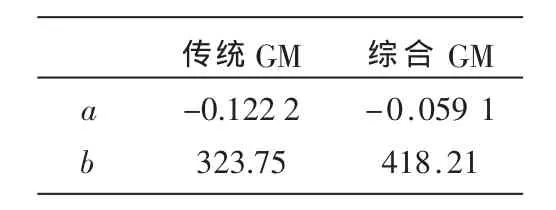
(6)根据结果对最优解进行更新。 如果 E(Ci+1) (7)Metroplis抽样稳定性的判别 如果 n (8)退火结束条件 如果 Eopt>Tk,则令 i=i+1;否则令 i=0。如果 i≥t或者Eopt<ε,则算法结束;否则继续步骤(9)。 (9)退火方案 按 Tk+1=ηTk,置 k=k+1,转步骤(2),其中 0<η<1。 (10)将 a、b代入式(2)的微分方程,并进行累加得到: 利用SA确定GM(1,1)模型参数的优点可以使 GM(1,1)模型在预测时,对选择参数具有存储和记忆能力,并能够将当前所得的最优参数进行更新,使得参数根据记忆调整方向[3],并且利用SA方法可以使得所选参数具有一定概率接受调整,从而跳出局部极小趋向全局极小的特性,提高了参数选择学习的速度和逼近系统的精度[4],提高了 GM(1,1)预测模型的通用性。 用Matlab利用上述提到的方法建模,对湖南省某县1992年~1999年的用电量数据进行仿真。采用均方百分比误差作为比较依据: 本文只选取历史负荷数据作为输入变量,以前5个历史值作为输入变量。结果如表1、表2所示,其中智能传统 GM(1,1)和 SAGM(1,1)的均方百分比误差 e分别为0.84%、1.01%。 表1 预测结果比较 表2 参数比较 对 GM(1,1)和模拟算法建模进行分析,针对各自的优缺点提出新的组合模型,并就改模型的建模思想和建模步骤进行了理论探讨。算例分析表明,此新型组合模型能较好地模拟负荷变化发展情况,有效提高负荷预测精度,并且能自动有效地优化 GM(1,1)学习参数,具有较强的使用价值。 [1]李瑾,刘金朋,王建军.采用支持向量机和模拟退火算法的中长期负荷预测方法 [J].中国电机工程学报,2011,31(16):63-66. [2]余健明,燕飞,杨文宇,等.中长期电力负荷预测的变权灰色组合预测模型[J].电网技术,2005,29(17). [3]周德强.基于最小一乘的 GM(1,1)模型及在负荷预测中的应用[J].电力系统保护与应用,2011,29(17). [4]张勇军,石辉,翟伟芳,等.基于层次分析法-灰色综合关联及多灰色模型组合建模的线损率预测 [J].电网技术,2911,35(6).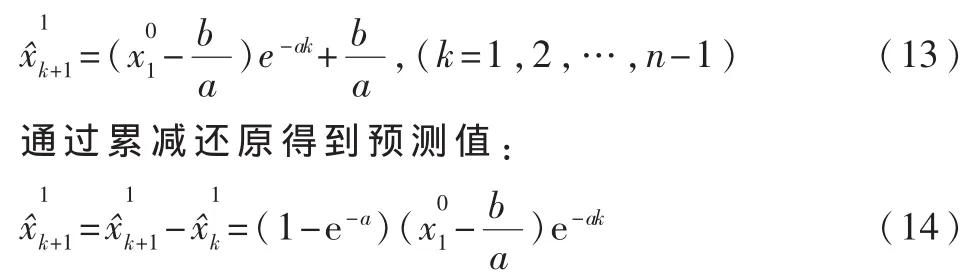
4 实例验证