一种模糊偏好排序的FJSP蚁群算法*

李欣娜，朱晶晶，樊文清

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

由于传统作业车间调度有很大的局限性，不能很好地贴合实际生产情况，对此学者们提出了柔性作业车间调度 FJSP（Flexible Job-shop Scheduling Problem），其允许工序由一组机器中的任意一台加工，且由于加工机器的性能差异，其加工时间长短也不同，使得调度的灵活性得到增加。

目前求解FJSP的研究主要集中在基于智能的启发式方法[1-3]。本文先将多目标问题转化为单目标问题，由于蚁群算法具有较强的鲁棒性和发现较好解的能力[4]，因此采用蚁群算法求解单目标问题。然后结合模糊属性权重对每个目标赋予不同的权重系数，以此来解决FJSP问题。

1 多目标FJSP问题的数学模型

1.1 FJSP问题描述

假定加工系统有M台设备和N个工件，每个工件包含一道或多道工序，工序顺序是预先确定的，每道工序可以在多台不同设备上加工。同一工件的工序之间有先后约束，不同工件的工序之间没有先后约束。每个工件在某一时刻只能在一台设备上加工，任一工件的工序必须顺序完成。调度目标是选择最佳的工序加工设备，并确定每台设备上工件的最佳加工顺序，使各工件的加工时间、关键设备负载和设备总负载最小。

1.2 符号变量说明

N为工件数量；M为设备数量；J为所有设备集合；Jij为工件 i（i=1，…，N）的第 j（j=1，…，Pi）道工序可选加工设备集，Jij⊆J；Pi为工件 i需加工的工序数；tijm为工件i的第 j道工序在设备 m（m⊆Jij）的加工时间；Sijm为工件i的第j道工序在设备 m上的开始时间；Eijm为工件 i的第j道工序在设备m上的完工时间；AEm为所有工件在设备m上完工的时间；AE为所有工件最后完工的时间；Fm为设备m的负载（所承载加工时间之和）；Fk为关键设备负荷；FT为设备总负荷。

1.3 目标函数

本文将多目标问题转换成如下三个单目标问题：

通过对各单目标问题的求解，采用三角模糊数的方法对所拆分的单目标问题进行整合，从而得出该FJSP多目标问题的最优解集。由于各单目标问题的单位并不相同，因此，需要对单目标问题的解进行规范化处理。对于成本型目标和收益型目标分别采用式（4）、（5）进行规范化。其中，fimax、fimin分别表示第 i目标的最大值和最小值，通常根据研究问题的特性来选定。

假设各单目标问题的模糊权重分别为 ω1、ω2、ω3，并通过对各单目标问题的无量纲化处理（在采用模糊权重的时候，是针对极大化目标函数，对于极小化问题可转化为极大化问题，令 fi′=-fi），可以得到该 FJSP多目标问题的最终的目标函数为：

1.4 约束条件

（1）工艺约束

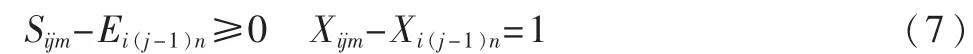
工件e的第j道工序必须在第j-1道工序完成后才能开始。

（2）独占约束

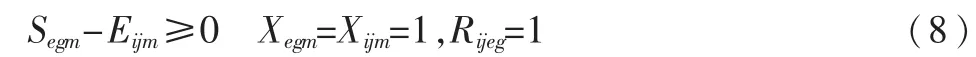
任一确定时刻，机器m不能同时加工任意两个不同的工件，也不能同时加工任意两道不同的工序。

2 蚁群算法解决多目标FJSP问题

2.1 状态转移规则

为了避免停滞现象的出现，蚁群算法采用了确定性选择和随机性选择相结合的选择策略，并在搜索过程中动态调整状态转移概率。即对位于加工工序σij的机器c 的蚂蚁 k 按式（9）选择机器 m 加工下一工序 σ（i+1）（j+1）：

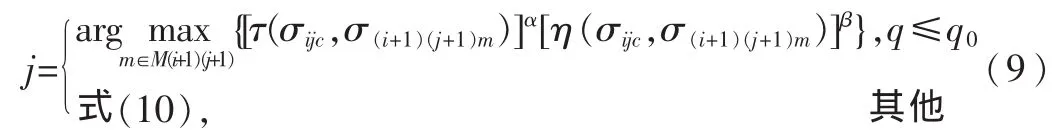
其中 ，M（i+1）（j+1）表 示 可 用 于 加 工 工 序 σ（i+1）（j+1）的 候选设备集合；τ（σijc，σ（i+1）（j+1）m）表示加工工序 σij的机器 c 与加工工序 σ（i+1）（j+1）的机器之间的信息素浓度；η（σijc，σ（i+1）（j+1）m）表示机器 c 加工完工序 σij后，由机器 m 加工工序 σ（i+1）（j+1）的期望程度；α表示信息素启发式因子；β表示期望启发式因子；q是一个在区间[0，1]内的随机数；q0是一个算法参数（0≤q0≤1）；当 q>q0时，蚂蚁 k 根据式（10）确定由机器 C向下转移用来加工工序 σ（i+1）（j+1）的目标设备：

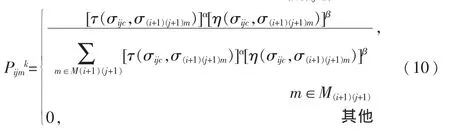
其中，求解关键设备负载最小以及设备总负载最小问题，其期望程度可采用式（11）；对于求解各工件的加工时间最小问题，期望程度可采用式（12）：

其 中 ，C（σ（i+1）（j+1）m，m）表 示 机 器 m 加 工 工 序 σ（i+1）（j+1）所 需的 负 载 ，CM（m）表 示 机 器 m 加 工 工 序 σ（i+1）（j+1）之 前 已 产 生的 负 载 ；t（σ（i+1）（j+1）m，m）表 示 机 器 m 加 工 工 序 σ（i+1）（j+1）所 需的 时 间 ，tM（m）表 示 加 工 工 序 σ（i+1）（j+1）前 机 器 m 上 所 完 成工序累计时间和式（9）所确定的蚂蚁转移到下一个设备的方法，称为自适应随机概率选择规则。在这种规则下，每当蚂蚁要选择向一个设备转移时，就产生一个在[0，1]范围内的随机数，根据这个随机数的大小按式（9）确定用哪种方法产生蚂蚁转移的方向。

2.2 信息素的更新规则

（1）全局更新规则

全局更新规则只为每一次循环中最优的蚂蚁使用。更新规则如式（13）：

其中，Cgb为蚁群当前循环中所求得的最小负载；tgb为蚁群当前循环中所求得的工件加工最短时间；ρ为一个（0，1）区间的参数，其意义相当于蚁群算法基本模型中的信息素挥发系数；Q为常量，表示蚂蚁循环一周或一个过程在所经过的路径上释放的信息素总量。

（2）局部更新规则

局部更新规则是在所有的蚂蚁完成一次转移后执行式（13），其中：

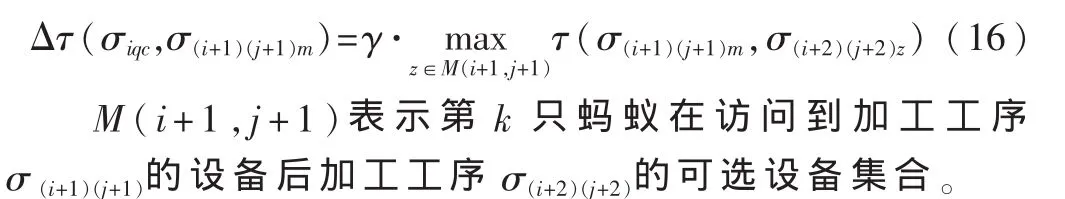
3模糊属性权重的确定

三角模糊数能够有效地克服评判过程中主观因素的影响，使多目标决策方法更客观、更准确地反映问题。因而本文采用三角模糊数将式（6）单目标问题整合成多目标，使得对FJSP问题的求解更加精准。

模糊属性权重的确定过程[5]如下：

（1）获得决策者的模糊评判信息。设决策者对各收益类目标评价 P={差，较差，一般，较好，好}，对成本类目标评价 C={高，较高，一般，较低，低}。

（2）将决策者的模糊评判信息转换为三角模糊数。利用语义函数 F （收益类指标/成本类指标）=（m1，m2，m3），将消费者的语言指标转换成三角模糊数的形式。F（好/低）=（0.8，1，1），F（较好/较低）=（0.6，0.75，0.9），F （ 一 般/一 般 ） =（0.35，0.5，0.65），F （ 较 差/较 高 ）=（0.2，0.35，0.5），F（差/高）=（0，0，0.2）。

（3）模糊属性权重的归一化处理。设给定的I个模糊权重 ωi=（ω1i，ω2i，ω3i），i=1，…，I归一化后的模糊属性权重为 ωi′=（ω1i′，ω2i′，ω3i′），则有：

β是一个预先设定的权值，它反映了均值和方差在模糊排序中的相对重要性，通常取β=0.5。

本文采用蚁群算法，结合模糊权重法，将车间工件加工的多目标问题转化为单目标问题，以此建立柔性作业车间调度模拟方案。得益于蚁群算法较好的鲁棒性和解的全局性，该方案在车间生产调度工作中能够较理想地满足实际加工的需求，使得生产调度更加合理化、统筹化、柔性化，从而节约生产成本，有利于生产效率的进一步提高。随着信息技术及经济的不断发展，利用基于智能优化算法的FJSP解决生产调度问题将会成为主流，而在此领域的探索与研究也将具有深远的意义。

[1] SHENG L， WeiXiaobin， WENY Z.Improved aco schedulingalgorithm based on flexible process [J].Transactions of Nanjing University of Aeronautics &Astronautics （S1005-1120），2006，23（2）：154-160.

[2]BRANDIMARTE P.Routing and scheduling in a flexible job shop by tabusearch[J].Annals of Operations Research，1993，22（2）：157-183.

[3] KACEM I.Genetic algorithm for theflexible job-shop scheduling problem [J].IEEE International Conference on Systems，Man，and Cybernetics，2003（4）：3464-3469.

[4]DORIGO M， MANIEZZO V， COLORNIA.Theant system：optimization by a colony of cooperating agents[J].IEEE Transactions on Systems， Man， and Cybernetics Part B （S1094-6977），1996， 26（1）：29-41.

[5]李世威，王建强，曾俊伟.一种模糊偏好排序的多目标粒子群算法[J].计算机应用研究，2011，28（2）：477-480.

[6] BONISSOE P P.A pattern recogition approach tothe problem of linguistic approximation in system analysis[A].IEEE 1976 International Conference on Cybernetics and Society[C].NewYork，USA： IEEE，1979.793-798.