调用氦物性程序对透平膨胀机叶轮S2流面正问题分析

刘晓东 庄 明 付 豹

(中国科学院等离子体物理研究所 合肥 230031)

1 引 言

氦透平膨胀机是大型氦低温系统的重要部件，为获取4.5 K温度级冷量冷却超导磁体及其它低温部件EAST低温循环系统采用了6个冷却级，分别是:液氮预冷级，第一级膨胀冷却级(膨胀机T1)，第二级膨胀冷却级(膨胀机T2)，节流路膨胀冷却级(膨胀机T3)，节流冷却级。其中T1和T2串联使用，而T3与T1、T2串联路并联使用。由于氦透平膨胀机的性能(运行稳定性与运行效率)对EAST低温系统起着至关重要的影响(影响其制冷系数)，又由于氦透平膨胀机T3叶轮进口参数处于高压、深低温区(接近两相区和超临界区)，此时工质氦不能看作理想气体，因此有必要用流线曲率法对低温氦透平膨胀机T3的叶轮流场进行研究。本文利用流线曲率法方法对低温氦透平膨胀机T3的叶轮的正命题进行研究。

氦透平膨胀机T3的设计进口压力Pi=0.968 MPa，进口温度Ti=7.86 K(下标i代表叶轮进口参数)，且预期达到出口压力Po=0.42 MPa，进口温度To=6.34 K(下标o代表叶轮出口参数);在进口条件下，工质氦接近两相区和超临界区，氦的压缩因子Zi=0.631 5，在出口条件下氦压缩因子 Zo=0.485 9，进出口氦的物性参数都远远偏离理想气体，因此在利用流线曲率法计算时，在处理氦透平膨胀机T3的叶轮膨胀工质氦时，必须按照非理想气体来进行。

吴仲华教授1952年发表论文“轴流、径流和混流式亚声速与超声速叶轮机械中三元流动的通用理论”［1］，提出了两类相对流面理论(S1流面和 S2流面)，把三元流动分解为两个流面上的二元流动问题来求解，为透平机械内部流动的计算奠定理论基础。

应用两类相对流面理论计算叶轮机械内部流场的方法有多种，其中工程界应用最多的是流线曲率法(因其控制方程的系数中包含有流线曲率，故而得名)。

流线曲率法有以下显著的特点:控制方程建立在R-Z坐标系下;不考虑由于流动损失直接引起的对速度控制方程的影响(速度方程按可逆过程推导);只把相关的影响，包括熵增或者压损考虑到热力状态参数的变化中;流动过程可逆绝热;S2流面为连续光滑的空间曲面。

流线曲率法的求解，一般分为正命题和反命题两类［2］。

正命题就是根据已有的叶轮叶片和轮盘形状，求解出叶轮内部流场。因此，正问题也可以称为性能分析问题。

反问题则反之，即根据规定的速度分布，设计出叶片形状。因此，反问题也可以称为设计问题。

本文对氦透平膨胀机T3叶轮S2流面正命题进行分析。

2 氦透平膨胀机叶轮流线曲率法正命题

2.1 控制方程

2.1.1 速度梯度方程［3］

利用龙哥库塔法则确定整个叶轮机械的速度场

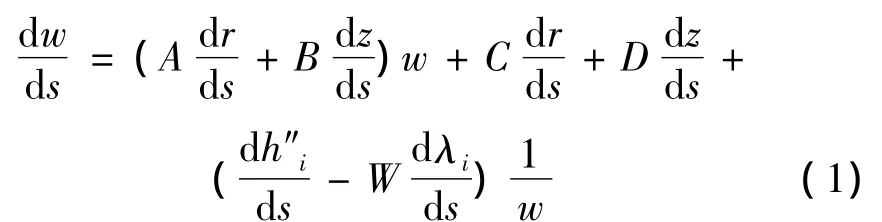
式中:

速度控制方程需要注意以下几点:

(2)β指的是流体的相对速度w与子午面的夹角，βb指的是透平叶轮叶片的安装角度;

(3)流面分离半径rb。当气流未流过分离半径rb，认为气流在叶片表面发生分离，平均相对流面和叶片型面不一致;一旦气流流过分离半径rb，平均相对流面与叶片型面重合。

分离半径rb的近似计算公式［3］一般采用:

式中:r0为透平叶轮进口半径;代表叶片数目，tθ代表叶片的切向厚度，tθ=tn，这里θb指的是透平机械叶片表面的角坐标)。

流面角坐标θ和叶片表面角坐标θb不总是一致［4］:这里涉及到，当流体氦进入叶轮时候，为保证流体能够顺利进入叶轮，所以流速会偏离叶片型面一定角度(β≠βb)，导致流面和叶片型面不一致(θ≠θb);而流过一段距离(r≠rb)时，流面和叶片型面一致(θ≠θb)。

2.1.2 流量方程

用来校核速度梯度方程生成的速度场的合理性，进而反过来修正速度场:

流量校核方程需要注意以下两点:

(1)假定氦透平膨胀机在膨胀过程中，既与外界绝热，又无损失存在，即为等熵膨胀(实际膨胀过程，产生不可逆熵增，为了保证准确性，把熵增考虑到压损［5］ΔP中，也就是在膨胀过程s保持不变);

(2)为确定流体氦的任意状态的物性参数，比如物性参数ρ(ρ=ρ(h，s))，必须知道其它两个独立的物性参数，在这里选择焓值h、熵值s，即焓值h、熵值s确定后，该点状态参数也就确定。

2.2 焓值h、熵值s的确定方法

熵值s与进口相同，即s=si;而任一点的焓值h，可由式(4)确定，

式中:w为任一点的相对速度;h″i为进口滞止焓;λi为进口预旋度;计算公式为:

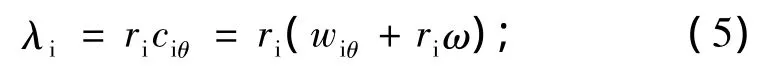
2.3 叶轮进口滞止焓的计算方法

推导过程

式中:βi为叶轮氦流体的进口流动角;ω为叶轮旋转角速度，r/min;wi为叶轮进口相对速度，m/s;ci为叶轮进口绝对速度，m/s;WTFL为氦透平膨胀机T3进口氦质量流量，kg/s;Ai为叶轮进口平均面积，m2为叶轮进口的滞止密度，kg/m3。

偏离理想气体低温氦的物性参数，如密度ρ不能利用完全气体公获取;本文将氦物性程序Hepak与主程序结合使用，一旦确定h、s，调用子程序Hepak即可获取密度值ρ。这里没有选用温度T作为已知参数，在高压，深低温下(7.86 K，0.986 MPa)，低温氦流体的比定压热容cp不能看作常数，也就是不能直接运用dh=cpdT来确定dT;所cp以直接使用焓值h作为已知参数。

3 EAST低温系统氦透平膨胀机T3叶轮工作流场分析

3.1 氦透平膨胀机T3的设计参数

氦透平膨胀机T3的设计参数如表1。

表1 氦透平膨胀机T3的设计参数Table 1 Design parameters of turbine expander(T3)

其它的输入参数包括:轮盘、轮盖型线坐标，叶片角坐标θ的分布，叶片法向厚度布表tn。盘盖型线轮廓以及初始假定流线如图1所示。叶片法向厚度分布表用于计算站厚度差值，如图2所示。

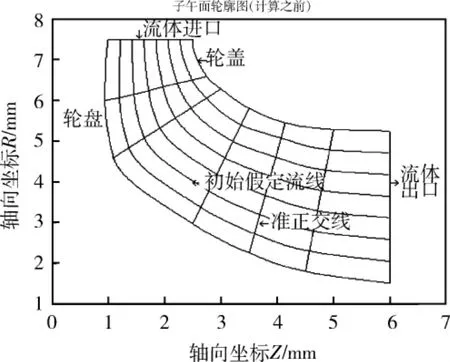
图1 叶轮子午面轮廓及准正交线Fig.1 Profile of meridian plane and Quasi-orthogonal lines about impeller

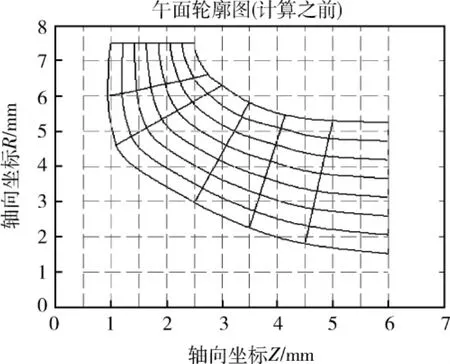
图2 叶片法向厚度分布表Fig.2 Table of normal blade thickness

3.2 氦透平膨胀机叶轮流场结果计算及分析

根据氦透平膨胀机T3叶轮的流体氦不能看作理想气体，编制出具体的叶轮流场计算程序，计算收敛后的叶轮流场流线如图3所示，图中显示了真实流线，明显与初始假定流线不一致。

图3 计算收敛后叶轮子午面流场Fig.3 Flow of meridian plane of impeller after convergence

3.2.1 叶轮内部流场不同位置处的相对速度

轮盘处，平均旋成面(中间叶高处)处的叶片吸力面、压力面和平均相对流面相对速度沿流线的变化曲线分别如图4、图5所示。

图4 轮盘处相对速度分布Fig.4 Relative velocity distribution for hub

在轮盘处，吸力面相对速度值最大，子午流面次之，压力面最小，这种分布规律与实际情况相符合。因为压力面是工作面，表面压力大;吸力面是非工作面，表面压力小;平均相对流面的压力介于两者之间。同理，平均旋成面处的速度分布与轮盘处的速度分布情况相似。

S2流面沿轮盘(叶根)、平均流线和轮盖(叶尖)3条流线的相对速度变化如图6所示。流线相同位置处，轮盖处相对速度最大，平均流线次之，轮盘处最小。

图5 平均旋成面处的相对速度分布Fig.5 Relative velocity distribution for mean surface of revolution

图6 S2流面3条典型流线相对速度分布Fig.6 Relative velocity distribution about three specific streamlines of S2surface

3.2.2 叶轮内部流场的压力、温度分析

流场计算收敛后，叶轮内部流场的压力，温度分别如图7和图8所示。如图7所示，低温氦流体沿着流动方向，压强一直处于下降状态，符合氦透平膨胀机的工作原理。对比表1，叶轮进口压强0.968 MPa，经过氦透平膨胀机膨胀后，压强降至0.42 MPa左右，对比进出口静压，该氦透平膨胀机叶轮符合设计要求。

如图8所示，叶轮进口温度7.86 K，经过氦透平膨胀机后，降至6.2 K左右，结合表1，对比进出口温度，该氦透平膨胀机叶轮符合设计要求，满足使用要求，并被EAST多轮实验所验证，从而进一步证明计算程序的可靠性与实用性。

图7 S2流面压力分布Fig.7 Pressure distribution of S2surface

图8 S2流面温度分布Fig.8 Temperature distribution of S2surface

4 结 论

利用流线曲率这一经典理论的正命题对一具体的低温氦透平膨胀机T3作了深入研究，得出如下结论:

氦透平膨胀机T3工作于高压、深低温区，则此工况下氦偏离理想气体，不能利用理想气体的性质来确定流体氦的密度ρ。为得到准确可信的结果，本文将氦的真实物性与主程序结合，得到了满意的的结果;

在流线曲率法中，子午面速度方程推导过程不考虑不可逆损失，也就是未考虑熵增，但是最后把不可逆损失考虑到物性参数中，本文考虑到压损ΔP，根据程序计算的结果，氦透平膨胀机T3满足EAST大型低温系统的要求，并被EAST多轮实验所验证，从而进一步证明计算程序的可靠性与实用性。

1 Wu Chung-Hua.A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial-Radial-and Mixed-Flow Types［R］.NACA TN 2604，1952.

2 孙正中.离心压缩机叶轮S2流面正反命题的研究［J］.风机技术，2007(6):12-17.

3 王尚锦.离心压缩机三元流动理论及应用［M］.西安:西安交通大学出版社，1991.

4 Katsanis Theodore.Use of arbitrary quasi-orthogonals for calculating flow distribution in the meridional plane 0f A turbomachine［R］.NASA TN D-2546，1964.

5 计光华.透平膨胀机［M］.西安:西安交通大学出版社，2006.