一种基于三元阵的水下目标被动定位方法

姜可宇，姚直象，尹敬湘

(海军工程大学 电子工程学院，武汉430033)

0 引言

利用水下运动目标的辐射噪声来检测和定位目标是潜艇隐蔽发现和攻击的一种重要手段。目前的被动测距方法主要有三元测距［1］、目标运动分析［2］和匹配场处理［3］3 种，其中三元被动测距法仍是潜艇声纳装备上普遍采用的被动测距方法，其关键是3 个子阵接收信号之间的两个时延估计。自1976年提出广义相关时延估计方法［4］以来，时延估计算法一直是信号处理领域的研究热点，根据不同的测量环境、信号特征，分别有不同的时延估计方法［1］，一般分为互相关法、相位谱法、自适应法和高阶统计量法等。这些方法都是以两个阵元接收信号的分析和处理为基础来估计时延。在实际的水声环境中，噪声干扰、多途效应和信道起伏等因素都会影响这些方法的时延估计精度［5］。在有限信号分析长度的情况下，随着信噪比的降低，噪声干扰对时延估计精度的影响非常明显。信号互双谱分析［6］在时域表现为3 个信号的互相关，称为三元相关分析。受信号互双谱分析的启发，本文提出一种基于三元互相关分析的水下目标被动检测和定位方法，该方法通过在二维时延平面上搜索相关峰来发现目标，并同时实现3 个子阵接收目标辐射噪声两个时延的估计。假设随机信号均值为0，且概率密度对称分布，则同一时刻两个不相关的随机信号极性相同的概率为50%，而3 个不相关的随机信号极性相同的概率只有25%，因此在利用三元相关估计随机噪声中的信号时延时，噪声的影响可以得到更多的抑制。

本文叙述了三元相关检测和定位原理，从理论上阐述了三元相关相对二元相关在目标检测上的优势，并通过仿真检验了三元相关相对二元相关在检测性能和时延差估计精度上的这种优势，探索了一条利用3 个子阵接收信号来估计一个时延的新思路。

1 三元阵被动检测与测距的数学模型

S 为声源。假设目标是点源，声波按球面波扩展。设有相邻阵元间隔为d 的三元阵，目标方位为θ，目标到各阵元的距离分别为r1、r2、r3.其中，r2即为要测定的目标距离r，假设目标与三元阵处于同一个水平面，如图1所示。

设声速为c，则两两阵元接收信号间的时延差分别为

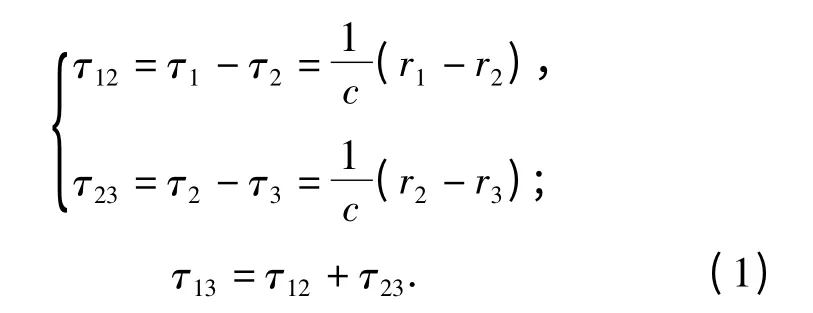
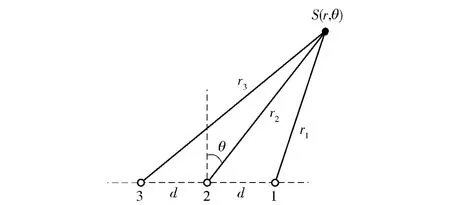
图1 三元阵被动测距模型Fig.1 Three-elements array passive ranging model

整理得到目标的方位和距离分别为

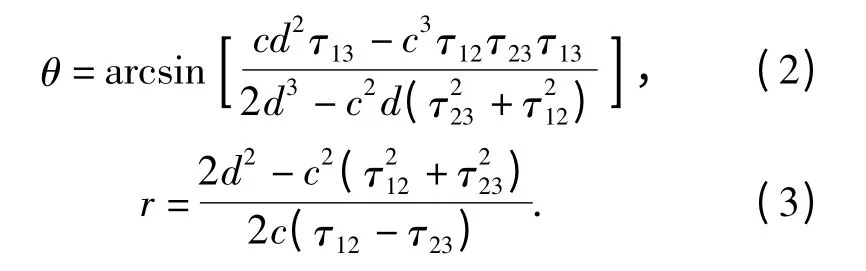
在利用二元信号相关的水下目标被动检测中，首先一般通过搜索阵元1 和阵元3 的互相关峰来发现目标。假设yi(n)表示第i 个阵元接收的信号，在无目标和有目标两种情况下，各阵元接收信号为

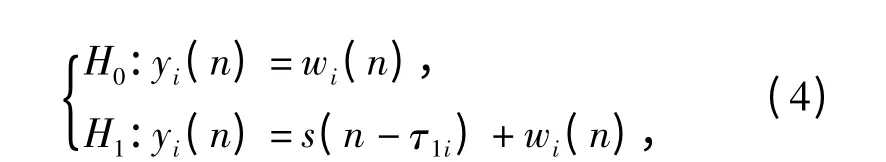
式中:s(n-τ1i)为第i 个阵元接收的目标辐射噪声，是s(n)的时延信号;wi(n)为第i 个阵元接收的背景干扰，假设它们之间相互独立，且与信号s(n)互不相关。

对于采样长度为T 的各阵元接收信号，二元相关检验统计量为

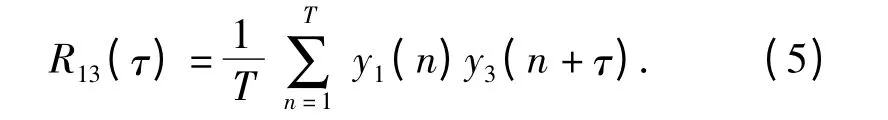
如果某个时延τm对应的检验统计量以较大概率大于附近其他时延对应检验统计量，即出现稳定的相关峰，则认为发现目标。

假设信号和噪声是平稳的，且噪声为白噪声，当接收信号无限长时，有

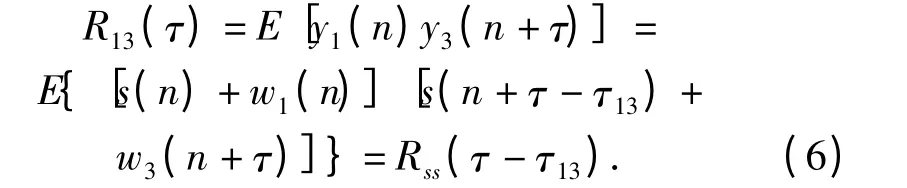
理论上，根据自相关函数特性，当τ =τ13时，目标辐射噪声自相关函数取最大值，相关峰对应时延即为需要估计的阵元1 和阵元3 之间的时延差τ13.同样，也可以估计出阵元2 和阵元3 之间的时延差τ23.将两个时延差代入(2)式、(3)式即可解算出目标所在位置。

实际中，由于噪声不一定是理想的高斯白噪声，实际观察信号也不可能无限长，噪声与信号间的互相关以及噪声间的互相关并不严格为0，导致时延的互相关估计出现误差。信噪比越低，噪声对时延估计的影响越严重。

2 新方法被动测距的基本原理

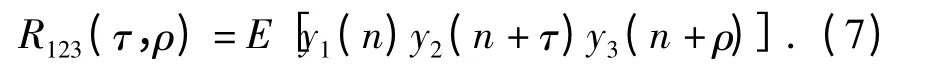
将上式展开，

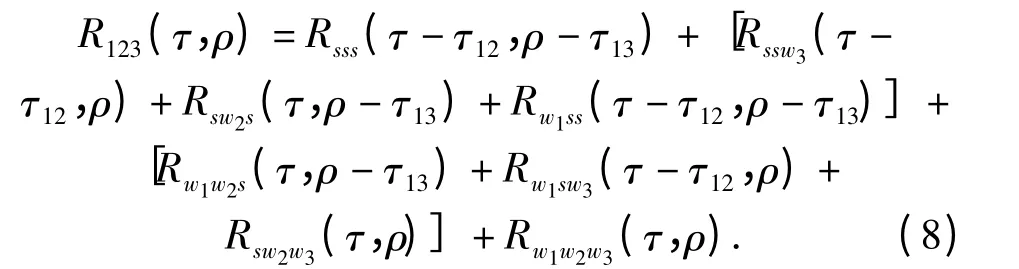
由于噪声之间相互独立，且与信号不相关，后7 项理论上为0，故(8)式变成

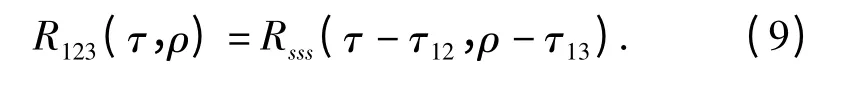
采样长度为T 的信号二维相关函数可表示为

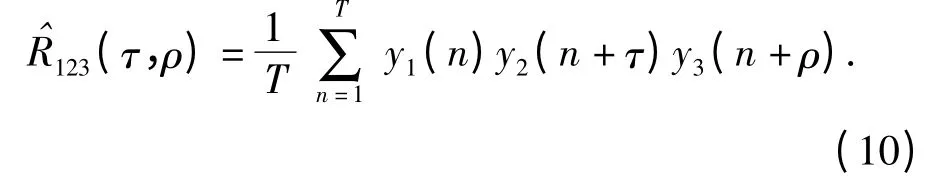
在二维相关函数平面上，找到相关峰后，其对应的两个时延值即为待估计的两个时延差^τ12和^τ13，进而求出^τ23，代入(2)式、(3)式解算出目标的方位和距离，这是三元相关法目标检测和定位的基本原理。

3 二元相关法与新方法检测性能理论分析

极性相关是减小信号相关运算量的一种常见处理方法。下面从极性相关的角度，对二元相关与新方法检测性能进行理论分析。

定义二元极性互相关函数为

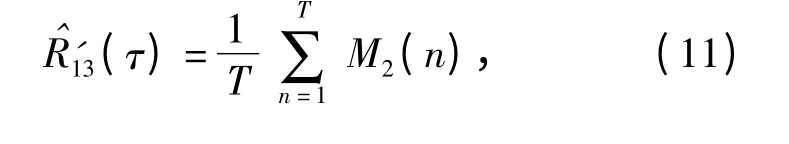
式中

M2极性相同;

定义三元极性相关函数

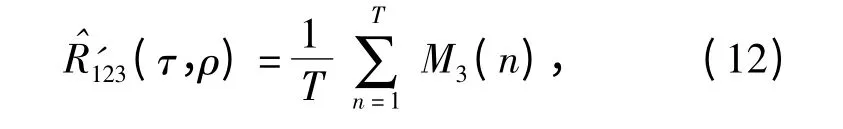
式中

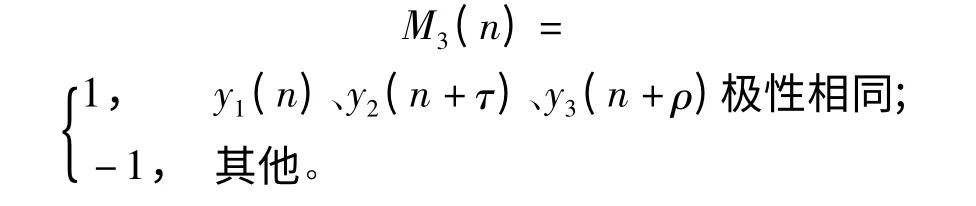
在无目标的情况下，独立的两路噪声在相同时刻极性相同的概率为50%，而独立的三路噪声极性相同的概率为25%，因此相比于二元相关检测法，噪声间的相关对三元相关检测的影响更小，从定性分析的角度来说，新方法的检测性能要好于二元相关检测法。

下面从理论上定量分析新方法相对二元相关在检测性能上的好处。假设采样后信号和噪声的分析长度为T，则在无目标情况下二元相关和三元相关输出分别为

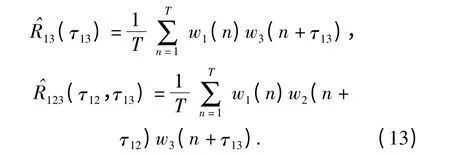
按(11)式、(12)式，无目标时输出极性相关值概率分布分别为

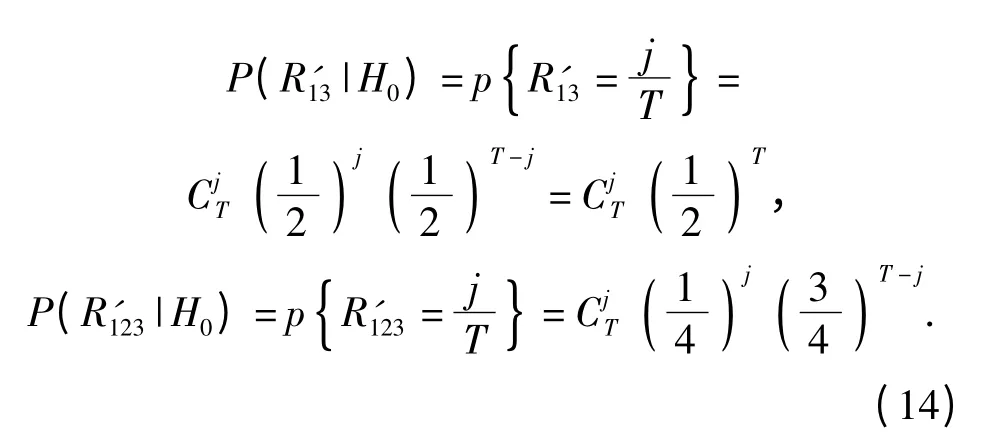
在有目标情况下，二元相关和三元相关输出分别为

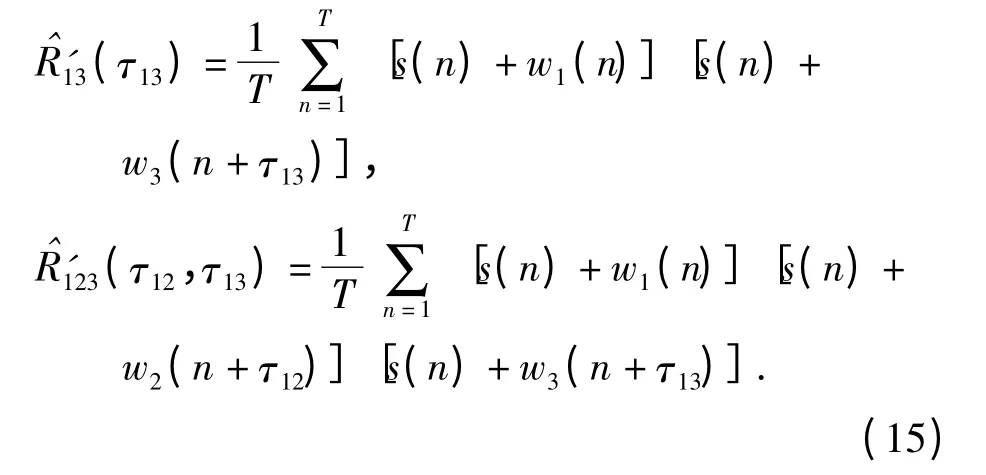
讨论叠加噪声后信号极性发生改变的概率，对信号s(n)，叠加噪声w1(n)、w2(n)和w3(n)后极性发生改变的概率相同，设为k(信噪比越低，k 越大，0 ＜k ＜0.5)。叠加噪声后两路信号极性相同概率为p=k2+(1 -k)2，三路信号极性相同概率为q=k3+(1 -k)3.按(13)式，输出极性相关值概率分布分别为

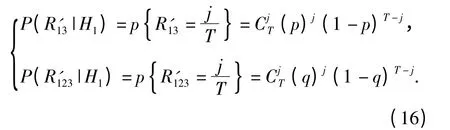
假设k=0.4，T=1 000，二元相关和三元相关的检测统计量的概率分布如图2所示。从中可以看出，在无目标情况下，二元相关输出均值和三元相关输出均值分别为0.5 和0.25，与前面的分析是相符的。依据纽曼皮尔逊准则，虚警概率取为10%，二元相关检测和三元相关检测的工作特性(ROC)曲线如图3所示。从该图可以看出，三元相关法比二元相关在检测性能上有大约2 dB 的改善。

由于三元相关检测法是在二维时延平面上搜索目标，因此其计算量比二元相关检测法大。三元相关检测法按(12)式对三路信号进行两个不同时延下的极性相关计算即可完成一定角度和距离上的检验统计量计算。经计算，当目标方位位于0°～60°，距离在2～20 km 之间时，时延对(τ13，τ12)分布于图4(a)中两条线之间，两条线之间的宽度如图4(b)所示，时延τ12的搜索空间大小τ'12分布在1～6之间。由此可以大致估计出三元相关检测计算量总体上大约是二元相关检测计算量的4～5 倍。

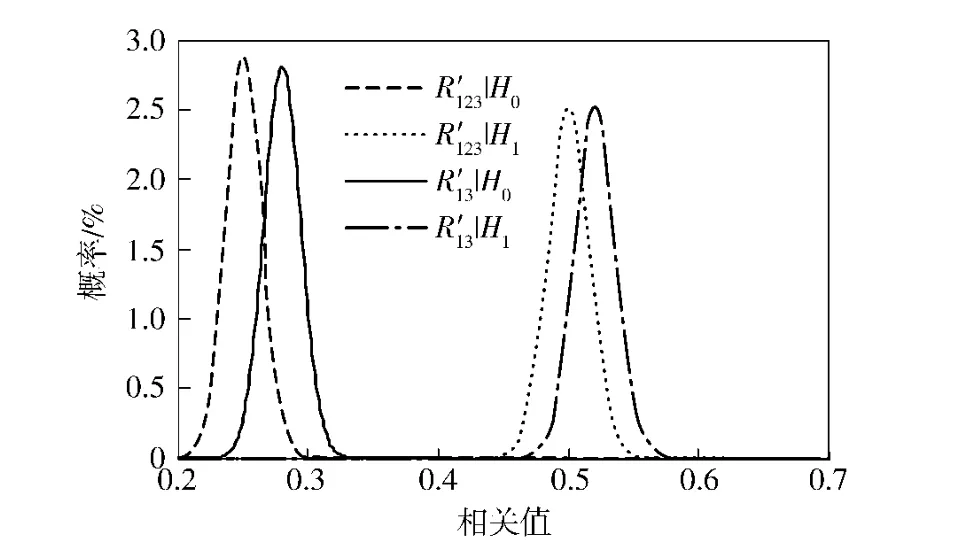
图2 两种相关检测输出的概率分布Fig.2 Probabilities of two correlation detecting methods

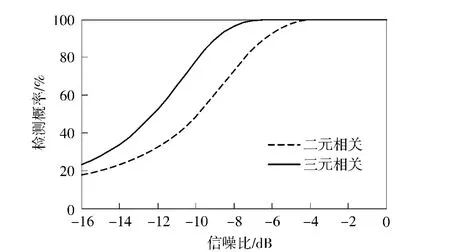
图3 两种相关方法检测ROC 曲线Fig.3 ROC curves of two correlation methods

4 仿真检验

采用蒙特卡洛方法给出新方法和二元相关法的ROC 曲线以及时延差估计性能曲线，比较二者在检测和时延差估计性能上的差异。

4.1 检测性能检验

假设三元阵相邻子阵间隔为20 m，信号采样频率为40 kHz，积分时间取1/40 s，每个信号的样本数为1 000.在方位5°、距离3 000 m 处有一噪声目标。为了仿真检验三元相关法相对二元相关法在检测性能上的改善，假设背景噪声和目标辐射噪声均为零均值白高斯噪声。经计算，目标辐射噪声到达3 个阵元的两个时延差分别为1.8 ms 和3.5 ms，经采样周期量化后的时延差分别为48 和93，目标辐射噪声按此量化后的时延差叠加到3 个子阵背景噪声中。

在每一个信噪比下，独立进行1 000 次仿真实验，目标检测ROC 曲线如图5所示。从图中给出的二元相关检测和三元相关检测ROC 曲线可以看出，与二元相关法相比，三元相关法在检测性能上具有约2 dB 的优势，这与理论分析的信噪比改善量是一致的。但是，无论是二元相关检测法还是三元相关检测法，仿真检测性能略好于理论分析检测性能。这可能与(14)式、(16)式的计算精度有关，因为大部分概率值很小，影响了两种相关法检测性能的统计。

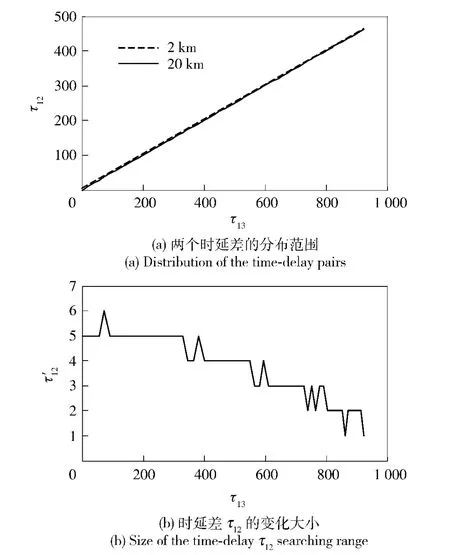
图4 时延对分布与时延搜索空间大小Fig.4 Time delay pairs distribution and size of time delay searching range

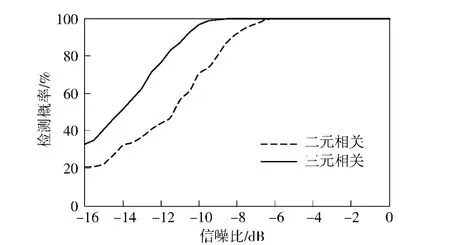
图5 目标仿真检测ROC 曲线Fig.5 ROC curves of target detection simulations

4.2 时延差估计

为与被动测距声纳的工作实际相一致，将检测性能检验中的背景噪声和目标辐射噪声均假设为带限色高斯噪声，频带为1 600～4 000 Hz，带内频谱为-6 dB/oct，积分时间取1 s，其他参数不变。时延τ13在83～103 范围内变化，时延τ12在如图4(a)所对应的范围内变化，以该范围内的三元相关函数最大值所对应时延差作为两个时延差的估计。在每一个信噪比下，利用二元相关法和三元相关法独立进行1 000 次时延估计仿真实验。二元相关法和三元相关法在每一个信噪比下时延差τ13估计误差的均方根值如图6所示。从仿真结果可以看出，在信噪比低于-13 dB 时，三元相关法的时延差估计误差均方根值比二元相关法平均减小约20 μs，根据定位误差与时延误差的关系式［7］

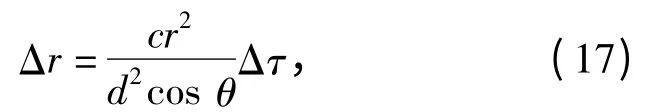
定位误差可以减小约675 m，当信噪比在-13～-5 dB 时，时延差估计误差的均方根值平均减小约2 μs，定位误差可以减小约68 m.

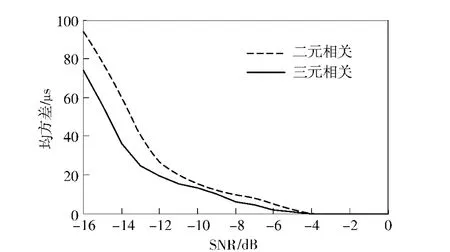
图6 时延差τ13估计的均方根值Fig.6 Time delay difference τ13estimation(r.m.s.)

5 结论

本文叙述了基于三元阵接收信号时延差测量的被动检测和测距原理，提出了基于3 个子阵接收信号间相关性度量的被动检测及时延差估计方法，从理论上分析了新方法相对二元相关法在检测性能上具有约2 dB 的优势，仿真结果验证了新方法相对二元相关法在检测性能和时延差估计精度上的提高。

References)

［1］ 宋新见.数字式噪声目标被动测距声纳研究［D］.哈尔滨:哈尔滨工程大学，2004.SONG Xin-jian.Study on digital noise targets passive ranging sonar［D］.Harbin:Harbin Engineering University，2004.(in Chinese)

［2］ 潘志坚，阎福旺，刘孟庵，等.纯方位水下目标运动分析方法研究［J］.声学学报，1997，22 (1):87 -92.PAN Zhi-jian，YAN Fu-wang，LIU Meng-an，et al.Method for bearings-only underwater target motion analysis［J］.Acta Acustica，1997，22 (1):87 -92.(in Chinese)

［3］ 杨坤德，马远良.匹配场噪声抑制的稳健方法［J］.兵工学报，2005，26(6):746 -750.YANG Kun-de，MA Yuan-liang.The robust approach of matched field noise suppression［J］.Acta Armamentarii，2005，26(6):746 -750.(in Chinese)

［4］ Knapp C H，Carter G C.The generalized correlation method for estimation of time delay［J］.IEEE Transaction on Acoustics Speech and Signal Processing，1976，24(4):1210 -1218.

［5］ 毛卫宁.水下被动定位方法回顾与展望［J］.东南大学学报，2001，31(6):129 -132.MAO Wei-ning.An overview of passive localization for underwater acoustics［J］.Journal of Southeast University，2001，31(6):129-132.(in Chinese)

［6］ 张贤达.时间序列分析［M］.北京:清华大学出版社，1996.ZHANG Xian-da.Time series analysis［M］.Beijing:Tsinghua University Press，1996.(in Chinese)

［7］ 侯自强，李贵斌.声纳信号处理［M］.北京:海洋出版社，1986.HOU Zi-qiang，LI Gui-bin.Sonar signal processing［M］.Beijing:Ocean Press，1986.(in Chinese)