炸药冲塞点火的数值模拟

张韩宇，段卓平，孙文遂，黄风雷

(北京理工大学 爆炸科学与技术国家重点实验室，北京100081)

0 引言

炸药冲塞试验(也称作大型跌落试验)是评价药柱同时受到撞击、剪切以及摩擦等力综合作用下炸药安全性的重要试验之一。国外从20 世纪80年代起开展此项工作的研究［1］，如美国洛斯阿拉莫斯实验室、海军水面作战中心等对PBX-9404、TNT、B-3 等炸药进行了冲塞试验。在国内，申春迎等［2］对高聚物粘结炸药进行了冲塞试验，得到了一些炸药发生点火的跌落高度以及对应的跌落撞击速度

数值计算方面，Frey［3］使用线粘塑性材料本构方程和阿累尼乌斯方程计算了炸药在剪切机械刺激下的点火反应，忽略了应力波的传播，计算模型为准稳态模型，并未反映出材料的力学不稳定性。随着损伤力学的发展，损伤变量引入到炸药非冲击点火模型之中，Bennett 等［4］建立了粘弹性统计裂纹力学模型(viso-SCRAM)，Todd 等［5］建立了损伤点火反应模型(DMGIR)，这两个模型均能较好地预测炸药在非冲击作用下的点火反应，但模型中损伤力学参数众多，需要大量试验获得相应参数，其推广使用尚需时日。炸药冲塞属于机械刺激范围，其特点为低强度、长脉冲。本文采用节点约束-分离方法、联合材料模型和化学动力学方程描述炸药冲塞过程和点火反应，考察单元尺寸对数值模拟的影响。

1 节点约束－分离方法

炸药冲塞点火问题是热-力-化耦合问题。炸药冲塞过程中单元承受较大的变形，易出现严重的网格畸变，炸药通常采用欧拉算法，它虽然可以解决网格的大变形问题，但不能够精确体现炸药破坏的物质边界，同时也影响炸药破坏面温度的描述。而传统的拉格朗日算法计算大变形和破坏会产生网格畸变，一般采用侵蚀算法，即将炸药设为连续介质，当炸药受到拉压后发生严重变形，达到指定数值后删除单元网格，这样可避免计算中出现网格畸变和负体积等问题，但这与实际炸药裂纹生成、扩展或者损伤断裂等有很大差别，且在删除单元后，炸药的热力学(温度)计算会发生错误而终止。因此，上述方法均不能有效解决炸药冲塞点火过程中的热-力-化耦合问题。

本文数值模拟中炸药材料采用节点约束-分离方法描述其力学破坏。节点约束-分离方法是指将节点按参与构成单元的个数进行复制，相邻单元坐标相同的节点相互独立，通过定义单元应变失效值对所有空间位置重叠的节点族进行“捆绑”［6］。当单元的应变达到指定失效值时，节点之间的约束失效，相邻单元坐标相同的节点相互分离。本文采用自编程序进行节点拆分，图1给出了本文计算实例中某4 个单元的节点约束-分离示意图。当达到单元应变失效值时，节点相互分离，单元演变成独立单元。在计算中设置自接触，单元之间不会发生穿透，单元碰撞时依然有相互作用。采用此方法时不需要删除炸药单元，材料仍采用拉格朗日算法，可以描述炸药的大变形、断裂破坏等现象以及宏观裂纹的生成、扩展，并支持炸药的热-力-化耦合计算。欧拉算法和传统的拉格朗日算法均不能有效解决炸药冲塞点火过程中的热-力-化耦合问题。

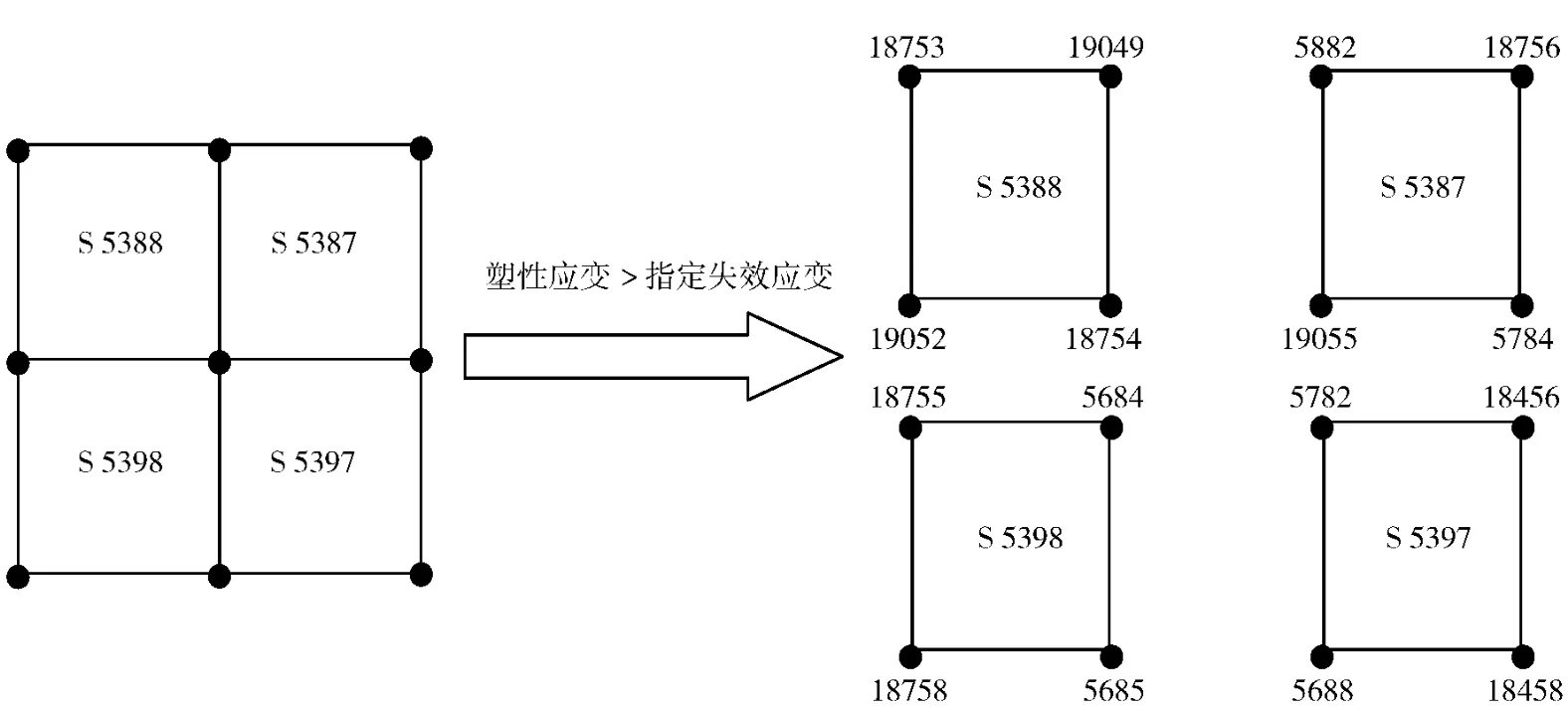
图1 4 个单元的节点约束-分离示意图Fig.1 Sketch map of node tie-breaking of four elements

2 数值计算模型

2.1 计算模型

文献［2］中试验装置如图2所示，炸药粘结在代用材料内，冲塞从钢板中间的孔穿过，整个试验件从高空跌落撞击靶板，冲塞钻入炸药，对炸药主要产生剪切和撞击作用。炸药尺寸为φ152 mm×102 mm，冲塞与炸药的接触直径为28 mm，冲塞长38 mm.试验测得PBX-2 炸药临界点火的跌落撞击速度为27.7 m/s，等效自由跌落高度为39.1 m.

采用LS-DYNA 有限元软件建立二维模型，计算模型采用拉格朗日算法。由图2可以看出，试验件为对称结构，1/2 计算模型如图3所示，采用轴对称实体单元划分网格，计算时直接将试件碰撞钢靶的跌落撞击速度加载于试验件上。根据最小单元尺寸由程序来设置结构计算的初始时间步长。为了热学计算的稳定性，人为设置热计算时间步长与结构计算时间步长相同，并设置步长缩放因子为0.67，确保数值计算稳定进行［7-8］。

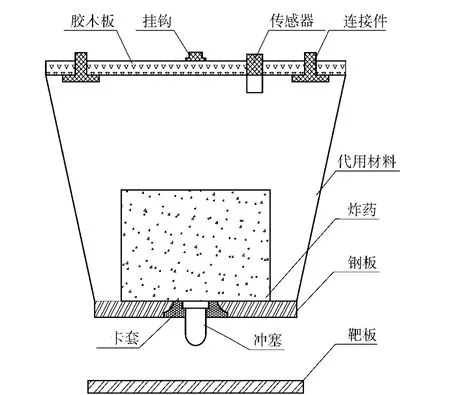
图2 炸药冲塞试验装置示意图Fig.2 Configuration of spigot test assembly

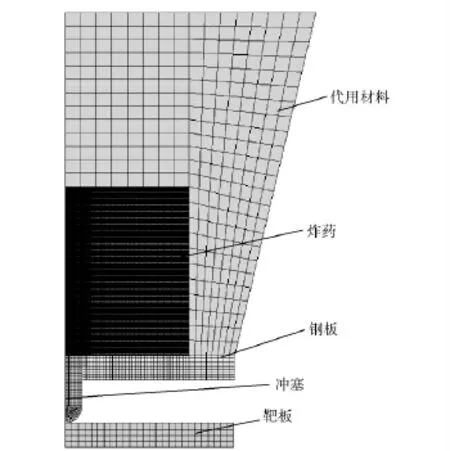
图3 炸药冲塞的1/2 计算模型Fig.3 1/2 calculation domain for spigot test

2.2 材料模型

炸药热-力-化耦合计算中，炸药材料模型包括力学模型和热学模型两部分。

炸药力学模型采用热弹塑性本构模型［8］描述。

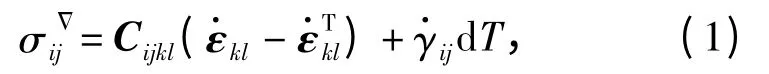
式中:T 为由炸药热弹塑性材料和热分解放热反应共同引起的炸药温度为总应变率;为热应变率，α 为线膨胀系数，δij为克罗内克符号;是与温度相关的弹性矩阵。

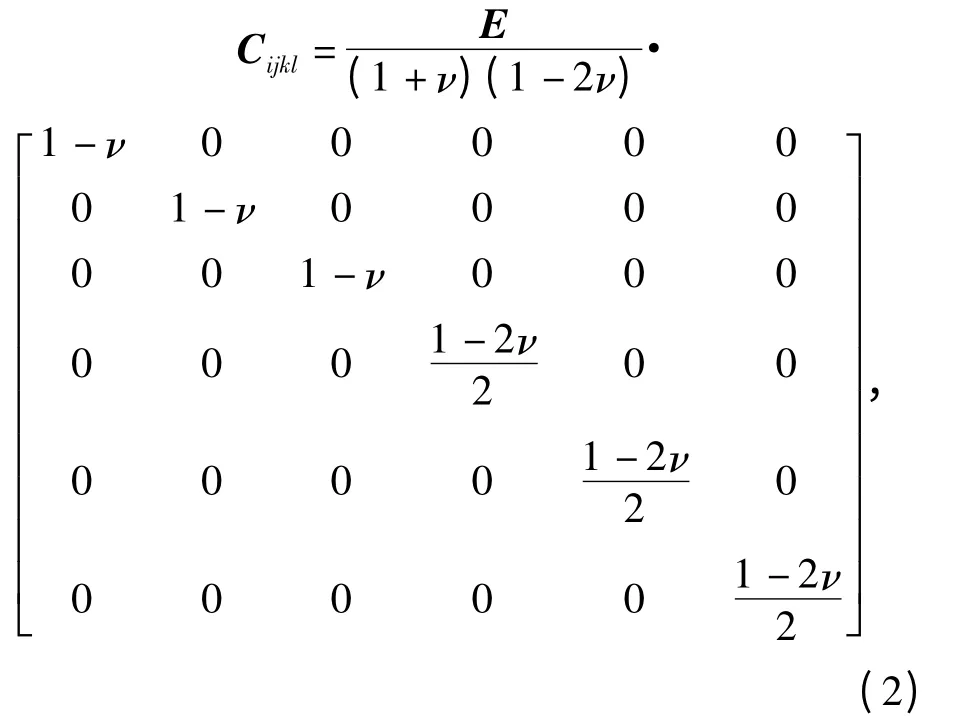
式中E、ν 分别为为杨氏模量和泊松比，与温度相关。

材料屈服函数为

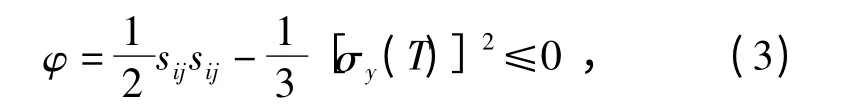
式中:sij为应力偏量;σy(T)=Ep(T)εpeff+σ0(T)为屈服应力;εpeff为等效塑性应变;σ0为初始屈服应力;Ep为塑性硬化模量，σ0和Ep均为温度的函数。

炸药热学模型采用各向同性热传导模型描述，热传导微分方程为

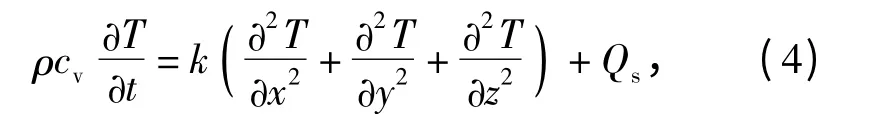
式中:ρ 为材料密度;cv为材料比热;k 为导热率;Qs为材料内部的热源，在此Qs=η σij+Qt，η 为功转热比率，Qt为放热量，如(5)式所示。

对于炸药材料而言，温度上升会引起材料的热分解放热反应，以阿累尼乌斯方程来表示炸药的热分解放热量。炸药热分解放热量为

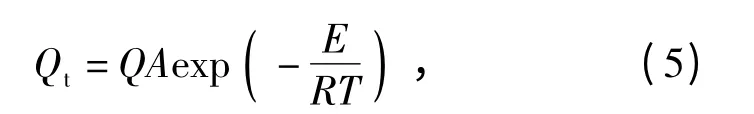
式中:Q 为反应热;A 为指前因子;E 为活化能;R 为气体常数。

代用材料、冲塞和靶板的热学模型均采用各向同性热传导模型描述，代用材料、冲塞和靶板的热学模型采用塑性随动硬化模型描述。PBX-2 炸药的热力学参数如表1所示，炸药失效应变为0.688%［9］.

3 计算结果

3.1 数值计算方法和材料模型适应性验证

图4给出了不同时刻炸药冲塞破坏和温度分布，图中的温度为炸药节点的温度，炸药单元的温度为该单元各个节点的平均温度。由图4可以看出，温度较高的区域基本位于冲塞破坏面，这是由于塑性功转化为热，热量在非常短的时间内聚集在材料局部区域。

表1 PBX-2 炸药热力学参数［10］Tab.1 Thermodynamic parameters of PBX-2［10］

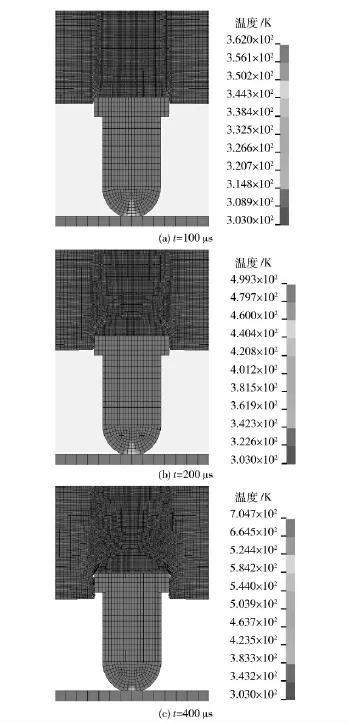
图4 不同时刻炸药冲塞破坏及温度(v=30 m/s)Fig.4 Evolutions of intrusion failure and temperature distributions of explosive (v=30 m/s)

图5为炸药的破坏情况，由图可以看出，使用节点约束-分离方法可以有效地避免网格发生畸变，而且能较好地模拟出炸药裂纹形成、破坏等力学行为。

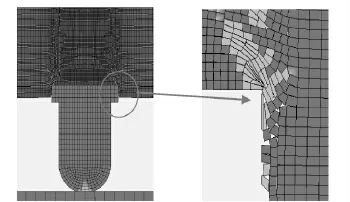
图5 炸药的节点分离和网格变形以及局部放大Fig.5 Node breaking and mesh deformation of explosive and close up of local surface

冲塞过程中，随着炸药温度的升高，热分解速率将遵循阿累尼乌斯规律迅速增加［3，11］。图6给出了跌落撞击速度为30 m/s 时计与不计化学动力学方程计算的炸药最高温度曲线对比。由图可知，计化学动力学方程计算炸药的温升时，在574 μs 时刻，炸药单元的温度曲线出现拐点，即dT/dt→∞，炸药开始发生点火反应，点火温度为770 K.不计化学动力学方程计算炸药的温升时，炸药温度虽然有一定的升高，但并没有出现温度拐点，炸药未发生点火反应。因此，模拟炸药点火反应需要计及炸药热分解放热反应对温升和点火的贡献。从上述数值计算可以看出，节点约束-分离方法、联合热弹塑性材料模型和化学动力学方程适用于描述炸药的冲塞破坏和点火反应，清晰地显示出炸药破坏面的形成，得到了炸药的点火温升曲线。

3.2 单元尺寸对数值模拟影响及临界速度确定

炸药冲塞破坏属于应变局部化问题，数值计算结果依赖于有限元网格密度［12］。下面考察0.4 mm、0.5 mm 和0.8 mm 3 种不同单元尺寸对冲塞破坏和温度分布等计算结果的影响。

图7为相同跌落撞击速度(v =36 m/s)条件下采用3 种不同单元尺寸计算的炸药冲塞破坏和温度分布(260 μs 时刻)。单元尺寸0.4 mm 时冲塞深度为7.4 mm;单元尺寸0.5 mm 时冲塞深度为7.5 mm;单元尺寸0.8 mm 时冲塞深度为7.6 mm.可以看出，破坏面形成和整体破坏效果比较一致，炸药的力学破坏受单元尺寸影响较小。但是破坏面上单元网格变形不同，引起的塑性变形温升也不同，单元尺寸对炸药冲塞破坏达到的最高温度有一定影响。

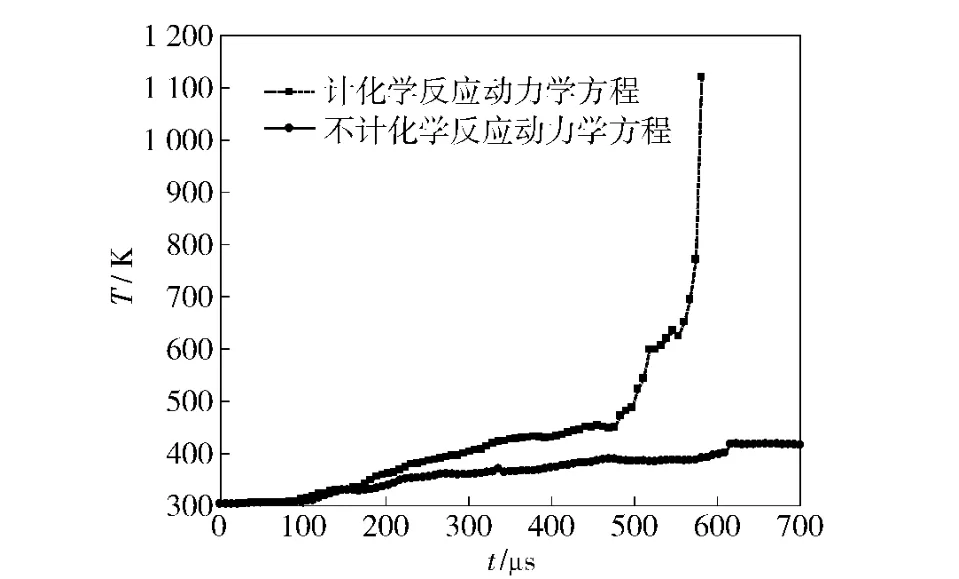
图6 计及/不计化学动力学方程计算的炸药最高温度曲线对比(v=30 m/s)Fig.6 Comparison of peak temperature of explosive from the models with/without chemical kinetics equation (v=30 m/s)

图8给出了相同跌落撞击速度(v =36 m/s)条件下3 种单元尺寸计算的炸药所能达到的最高温度对比。单元尺寸0.4 mm 时点火时间308 μs，点火温度为765 K;单元尺寸0.5 mm 时点火时间336 μs，点火温度为758 K;单元尺寸0.8 mm 时点火时间为434 μs，点火温度为731 K.可以看出，随着网格加密，单元尺寸越小，温升越快，炸药点火时间越短。

从计算耗费的时间来看，单元尺寸0.4 mm 耗费机时约为131 min，单元尺寸0.5 mm 耗费机时约为65 min，单元尺寸0.8 mm 耗费机时约为22 min.单元尺寸越小，花费的时间将成倍增加。

图9给出了单元尺寸为0.4 mm 计算32 m/s、30 m/s、29 m/s 3 种跌落撞击速度下炸药最高温度的曲线对比。可以看出，跌落撞击速度越大，炸药的温升越高。当跌落撞击速度为32 m/s 时，点火时间为406 μs，点火温度为756 K;跌落撞击速度为30 m/s时，点火时间574 μs，点火温度为770 K;跌落撞击速度为29 m/s 时，炸药未发生点火反应，因此，单元尺寸0.4 mm 下炸药冲塞点火的最小跌落撞击速度约为29.5 m/s.另外，单元尺寸0.5 mm 的最小跌落撞击速度为31.5 m/s，单元尺寸0.8 mm 的最小跌落撞击速度为35.5 m/s.单元尺寸0.4 mm 和0.5 mm 计算的点火反应和最小跌落撞击速度趋于一致。对比3 种单元尺寸下炸药冲塞破坏、点火反应、计算机时以及最小跌落撞击速度来看，单元尺寸0.4 mm 计算结果已基本消除了网格尺寸带来的计算误差，能够反应PBX-2 炸药冲塞过程中的力学破坏和点火反应。因此得到炸药冲塞点火的最小跌落撞击速度为29.5 m/s，与试验测得的临界跌落撞击速度为27.7 m/s［3］吻合较好。

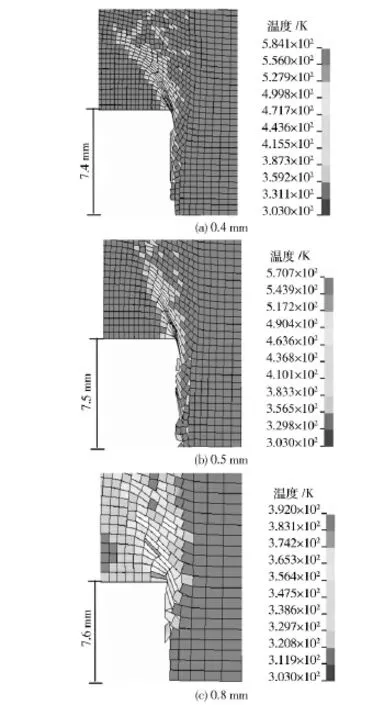
图7 3 种单元尺寸计算的炸药冲塞破坏和温度分布对比(v=36 m/s，t=260 μs)Fig.7 Comparison of intrusion failures and temperature distributions of explosive with three different sizes of elements(v=36 m/s，t=260 μs)

计算结果与试验结果相比略高，这是由于数值模拟采用的材料模型仅考虑炸药冲塞过程中塑性功转热引起的炸药温升，而没有考虑材料裂纹之间摩擦生热等对炸药温升的贡献。

4 结论

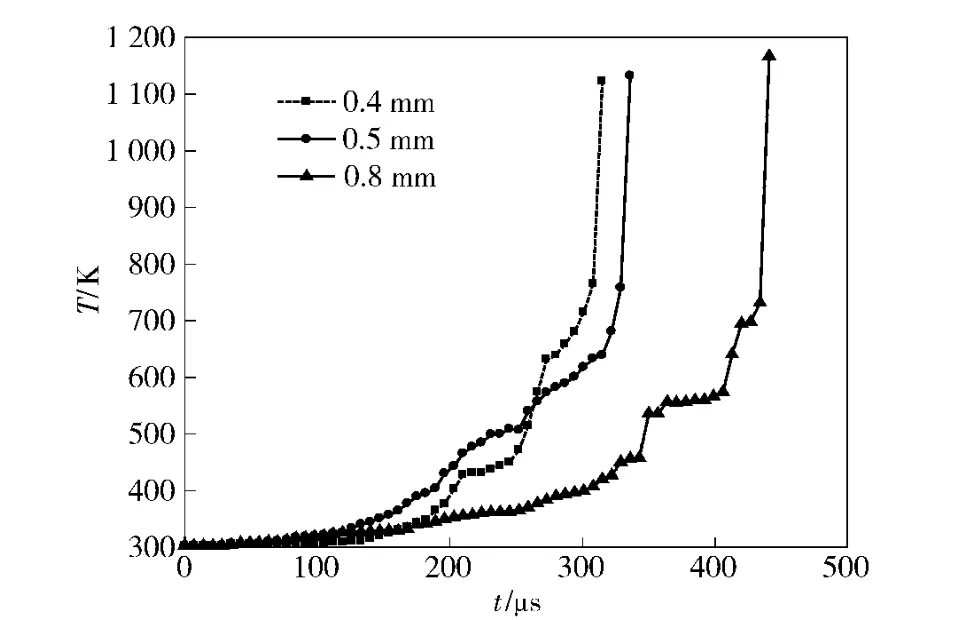
图8 3 种单元尺寸计算的炸药最高温度曲线对比(v=36 m/s)Fig.8 Comparison of peak temperature of explosive with three different sizes of elements (v=36 m/s)

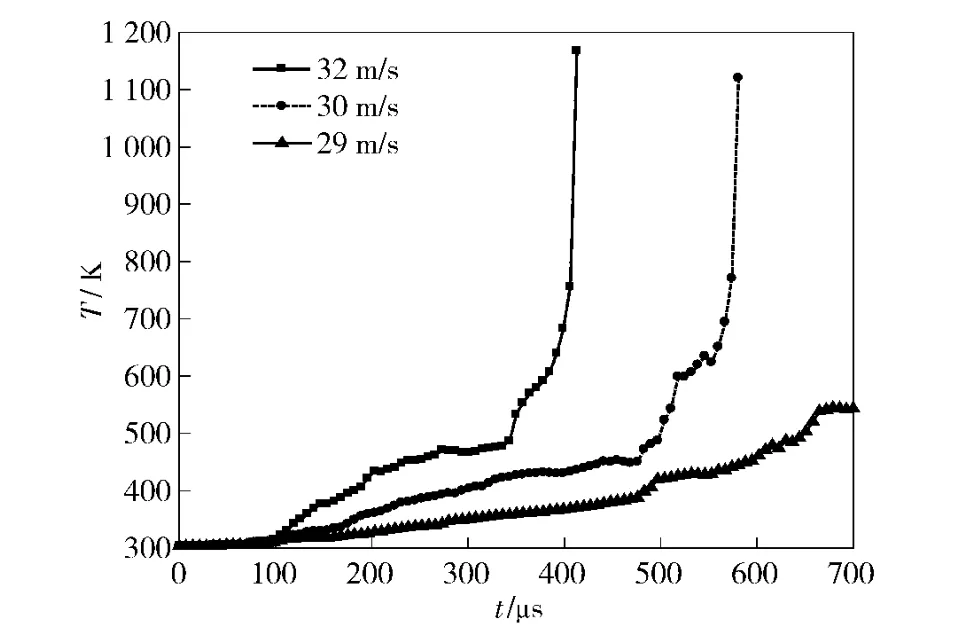
图9 3 种跌落撞击速度条件下的炸药最高温度曲线对比Fig.9 Comparison of peak temperature of explosive calculated with three different drop velocities

1)采用节点约束-分离方法、联合热弹塑性材料模型和化学动力学方程对炸药冲塞点火反应进行了数值模拟，该方法和模型能够有效地描述炸药冲塞破坏过程和点火反应。

2)数值计算中，单元尺寸对炸药冲塞过程中的力学破坏影响较小，但对炸药温升、点火反应以及临界跌落撞击速度有较大影响。对比0.4 mm、0.5 mm和0.8 mm 3 种单元尺寸的计算结果，单元尺寸0.4 mm 的计算结果能够反应PBX-2 炸药冲塞过程中的力学破坏和点火反应，并与试验结果比较吻合。

References)

［1］ Lee P R.Hazard assessment of explosives and propellants［M］∥Zukas J A，Walters W P.Explosive effects and applications.New York:Springer Press，1997.

［2］ 申春迎，向永，代晓淦，等.高聚物黏结炸药的冲塞试验研究［J］.火炸药学报，2010，33(2):29 -32.SHEN Chun-ying，XIANG Yong，DAI Xiao-gan，et al.Study on the spigot test of polymer bonded explosives［J］.Chinese Journal of Explosives and Propellants，2010，33(2):29 -32.(in Chinese)

［3］ Frey R B.The initiation of explosive charges by rapid shear［C］∥Proceedings of the 7th Symposium (International)on Detonation.Annapolis，USA:Office of Naval Research，1981:36 -42.

［4］ Bennett J G，Haberman K S，Johnson J N，et al.A constitutive model for the non-shock ignition and mechanical response of high explosives［J］.Journal of the Mechanics and Physics of Solids，1998，46(12):2303 -2322.

［5］ Todd S N.Non-shock initiation model for plastic bonded explosive PBX-5:theoretical results［J］.Shock Compression of Condensed Matter，2007，955(1):1006 -1009.

［6］ 张晓天，贾光辉，黄海.基于节点分离Lagrange 有限元方法的超高速碰撞碎片云数值模拟［J］.爆炸与冲击，2010，30(5):499 -504.ZHANG Xiao-tian，JIA Guang-hui，HUANG Hai.Simulation of hypervelocity-impact debris clouds using a Lagrange FEM with node separation［J］.Explosive and Shock Waves，2010，30(5):499 -504.(in Chinese)

［7］ 恽寿容，涂侯杰.爆炸力学计算方法［M］.北京:北京理工大学出版社，1995.YUN Shou-rong，TU Hou-jie.Explosion mechanics calculation method［M］.Beijing:Beijing Institute of Technology Press，1995.(in Chinese)

［8］ Hallquist J O.Ls-dyna theory manual［M］.Livermore，USA:Lawrence Livermore National Laboratory，2006.

［9］ 罗景润.PBX 的损伤、断裂及本构关系研究［D］.绵阳:中国工程物理研究院，2001.LUO Jing-run.Study on damage，fracture and constitutive relation of PBX［D］.Mianyang:China Academy of Engineering Physics，2001.(in Chinese)

［10］ 董海山，周芬芬.高能炸药及相关物性能［M］.北京:科学出版社，1989.DONG Hai-shan，ZHOU Fen-fen.Properties of high explosives and related materials［M］.Beijing:Science Press，1989.(in Chinese)

［11］ 孙宝平，段卓平，黄风雷.炸药摩擦点火评价实验数值模拟［J］.北京理工大学学报，2011，31(6):638 -642.SUN Bao-ping，DUAN Zhuo-ping，HUANG Feng-lei.Numerical simulation for assessment test of friction ignition in solid explosive［J］.Transaction of Beijing Institute of Technology，2011，31(6):638 -642.(in Chinese)

［12］ Needleman A.Material rate dependence and mesh sensitivity in localization problems［J］.Computer Methods in Applied Mechanics and Engineering，1988，67:69 -85.