斜轴式液压变压器变压比的影响因素分析

李雪原，苑士华，胡纪滨，魏超

(北京理工大学 车辆传动重点试验室，北京100081)

0 引言

恒压网络二次调节系统常采用减压阀来驱动直动执行机构，使用变排量的二次元件来驱动旋转执行机构，因此与传统的流量耦联液压系统相比，其具有节能、响应速度快、控制方便等优点，具有广阔的发展前景 。然而，受到二次元件造价昂贵，减压阀只能减压不能升压且功率损失大等劣势的影响，恒压网络二次调节系统目前难以得到推广［3-4］。液压变压器便是在这种环境下应运而生，其可以替代减压阀来驱动直动元件，而且不但可以降压也可以升压，效率也更高;其也可以与定排量的液压元件相结合联合驱动旋转元件，充当二次元件的角色，价格也更低廉。为此，伴随液压变压器的成熟，恒压网络二次调节系统的市场竞争力必将越来越强。目前，国内外对液压变压器的研究主要集中在液压变压器的结构方案、伺服控制和应用上，而对变压比特性影响因素及影响规律的研究相对较少［3-6］。因此，本文针对影响液压变压器变压比的因素进行分析，探索其影响规律，其不但具有重要的理论价值，而且也将对液压变压器的工程设计与应用提供理论指导，具有重要的现实意义。

1 斜轴式液压变压器变压比数学模型

本文针对斜轴式柱塞马达改造而成的液压变压器开展研究分析。改造过程中将配流盘的两个配流窗口改成为均布的3 个配流窗口A、B 和T 口，其中A 口为高压供油口，B 口为负载口，T 口为低压补油口。图1给出了斜轴式液压变压器配流盘各槽口角度与转角之间的对应关系。

图1 配流盘各配油窗口的角度关系Fig.1 Wrap angle relationship of valve plate

1.1 各槽口的排量模型

由图1可以看出，各参数之间存在如下关系

式中:φ1，φ2，φ3分别为腰形孔的边界角(°);θ 为配流盘相对于下死点的转动角(°);αA，αB，αT分别为配流口A、B、T 的有效包角(°)，且满足αA+ αB+αT=360°.

由柱塞的运动学分析可求得液压变压器配流盘三槽口A、B、T 的排量(m3/rad):

式中K=ZrAsinβ，其中Z 为斜轴式液压变压器的柱塞数;A 为柱塞孔的截面积(m2);r 为连杆球头在主轴盘上的分布圆半径;β 为驱动轴和缸体中心线之间的夹角。由(1)式～(6)式可得

1.2 各槽口的转矩模型

根据液压变压器的工作原理，A-T 两油口的组合可看作马达，把B-T 两油口的组合可看作液压泵，于是可得A 口理论输出转矩

式中ΔpAT=pA-pT.

A 口实际输出转矩

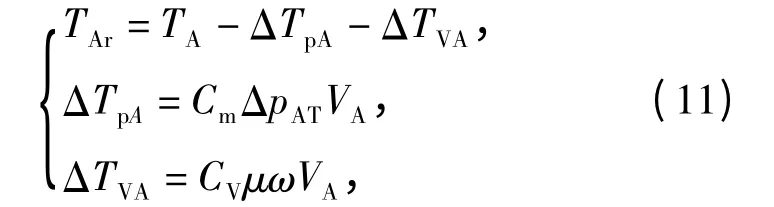
式中:ΔTpA为由压力引起的摩擦转矩损失;ΔTVA为由介质粘度引起的摩擦转矩损失;Cm为机械摩擦转矩损失系数;CV为粘性摩擦转矩损失系数。

B 口理论输入转矩:

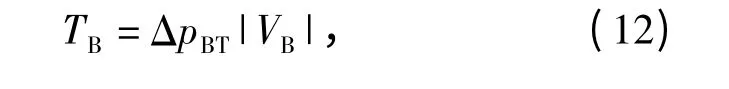
式中，ΔpBT= |pB-pT|.

B 口实际输出转矩

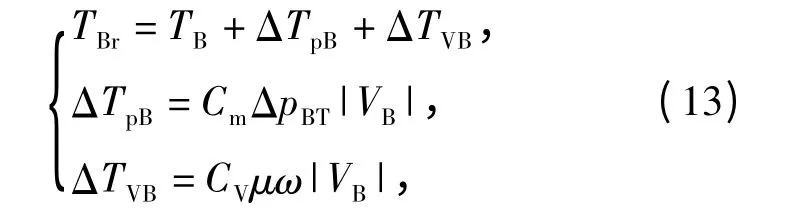
式中:ΔTpB为由压力引起的摩擦转矩损失;ΔTVB为由介质粘度引起的摩擦转矩损失。

1.3 液压变压器的变压比模型

斜轴式液压变压器在以一定的转速稳定工作时，液压变压器3 个油口处的油液作用在缸体上的力矩是平衡的，此时满足

结合(11)式和(12)式可得到液压变压器的负载口(B 口)的压力与进油口(A 口)的压力比值，其即为液压变压器的变压比

式中:Cl为液压变压器层流泄漏系数;μ 为工作油液的动力粘度(Pa·s)。则变压比公式改写为以负载流量为变量的等式，

上述液压变压器的变压比公式形式复杂，不便于利用。这里取层流漏损系数Cl=3.29 ×10-8、粘性摩擦损失系数CV=205 700 和机械摩擦损失系数Cm=0.076 16，并根据量纲关系对液压变压器的变压比公式进行简化，简化结果如(18)式和(19)式。(18)式中的核心变量是缸体转速ω，(19)式中的核心变量为负载口实际流量QBr.

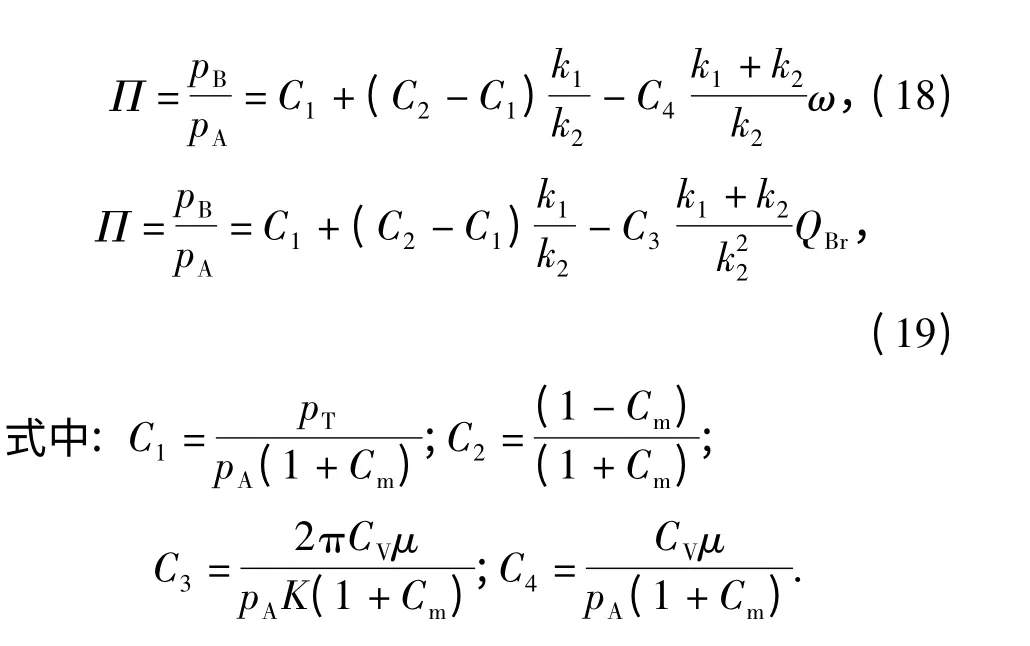
2 液压变压器的影响因素分析

2.1 补油口(T 口)压力对变压比的影响

T 口作为液压变压器的一个特殊的油口，它在液压变压器的配流盘处于不同的工作位置时所起到的作用是不同的，有时起到的是补油作用，有时起到的是排油作用。T 口工作压力pT对变压比的影响可直接根据变压比公式求导得出其规律，根据液压变压器变压比的简化(18)式可以推导出下述表达式，

根据(20)式可得dΠ/dpT随配流盘转角的变化曲线(如图2)，结合公式与曲线可以看出:1)当k2=k1时，dΠ/dpT=0，配流盘转角θ =αB/2，此时液压变压器的A 口排量等于B 口排量，T 口排量为0，因而pT的改变对变压比没有任何影响;2)当k2＞k1时，dΠ/dpT＞0，配流盘转角θ ＜αB/2，此时T 口为吸油口，理想时A 口与T 口的功率和等于B 口功率，因此pT越大，变压比也就会越大;3)当k2＜k1时，dΠ/dpT＜0，配流盘转角θ ＞αB/2，此时T 口为回油口，情况与前述相反;4)配流盘转角θ 至αB/2 这个角度位置越远，则T 口油压对变压比的影响就越明显，其主要原因是:角度偏离越远，T 口排量绝对值越大，所以在相同pT条件下，由T 口产生的力矩就越大，致使对变压比的影响相对就越明显。

图2 dΠ/dpT 随配流盘转角变化曲线Fig.2 Curve of dΠ/dpT vs angle of valve plate

2.2 负载口(B 口)流量对变压比的影响

若要保证液压变压器变压特性的稳定性，对变压比的干扰因素研究是必不可少的，其中很重要的一个干扰因素便是负载流量(缸体转速)的变化。

为分析转速对变压比的影响特性，可将变压比(18)式对转速进行求导

由(21)式可知dΠ/dω ＜0，故对于所有的斜轴式液压变压器，在其他参数不变的情况下液压变压器转速的升高会导致变压器变压比的减小。

图3(a)是以液压变压器缸体的转速和配流盘的转角为变量的液压变压器等变压比仿真曲线图，仿真参数取值为αA=αB=αT=120°，pA=10 MPa，pT=0.5 MPa，μ =0.03 Pa·s.由图中曲线可以更详细地看出，当配流盘转角不变时，液压变压器的缸体转速增加将使液压变压器的变压比随之降低。其原因是当配流盘转角不变时，缸体转速的升高将使液压变压器的粘性摩擦转矩损失增大，致使变压比跟着降低。

图3(b)是相同条件下以缸体负载口的实际流量和配流盘转角为变量的等变压比曲线。比较图3(a)与3(b)可知，输出流量对变压比的影响趋势与转速对变压比的影响趋势基本一致。究其原因，主要在于输出流量与缸体转速接近线性关系。

2.3 油液粘度对变压比的影响

在任何一个液压系统中油液的粘度都属于重要参数，在此我们通过将变压比(19)式对粘度进行求导，分析粘度对变压比的影响。

由(22)式可知dΠ/dμ ＜0，故对于所有的斜轴式液压变压器，在其他参数不变的情况下油温升高则会导致液压变压器的变压比增大。

图4反映出了油液粘度对变压比的影响特性，其中pA=10 MPa，pT=0.5 MPa，由曲线可以看出:在配流盘转角不变时，粘度减小，粘性摩擦转矩减小，从而使得液压变压器的变压比升高，反之相反，而且在配流盘转动角度越大时影响越明显。

图3 等变压比曲线Fig.3 Curve of transformer ratio hill

图4 油液粘度变化对变压比的影响Fig.4 Influence of transformer ratio vs viscosity

3 试验验证

图5为由斜轴式轴向柱塞马达改造而成的液压变压器实物照片。图6为在各项参数相同的情况下，仿真和试验所得的液压变压器变压比对比图形和对比曲线。图6(a)与图6(b)为变压比随配流盘转角与负载口流量变化的理论与试验图形，图6(c)为不同输出流量下变压比的理论与试验曲线。

图5 斜轴式液压变压器实物照片Fig.5 Photo of angle type hydraulic transformer

对比仿真与试验曲线可知，其趋势基本相同。另外还发现，在输出流量相对较大时，当配流盘转角大到一定值时，变压比曲线上会有一个转折点，配流盘转角在该转折点之前，变压比随着配流盘转角的增大而增大;而在转折点之后，变压比却随着配流盘转角的增大而减小，也就是说，液压变压器变压过程中存在一个最大变压比点，而且液压变压器的输出流量越大，最大变压比点出现越早。之所以会有这种现象，是由于当输出流量较大时，变压器缸体的转速非常高，因此其粘性摩擦与机械摩擦占据了主导地位，使得有用的输出压力降低、变压比减小。

4 结论

本文利用变压比公式对影响因素进行求导的方法，分析了补油口压力、负载口流量以及油液粘度对变压比的影响特性，其主要结论如下:

1)当配流盘转角θ =αB/2，T 口排量为0，pT的改变对变压比没有任何影响;当θ ＜αB/2 时，T 口为吸油口，A 口与T 口的功率和等于B 口功率，因此pT越大，变压比越大;当θ ＞αB/2 时，此时T 口为回油口，情况与前述相反。

2)由于dΠ/dω ＜0，故对于所有的斜轴式液压变压器，在其他因素一定时，缸体转速的升高会导致液压变压器的变压比减小。其物理原因在于:缸体转速的升高使液压变压器的粘性摩擦转矩损失增大，其导致变压比降低。

图6 负载口流量对变压比的影响曲线Fig.6 Influence of load circuit vs transformer ratio

3)由于dΠ/dμ ＜0，故对于所有的斜轴式液压变压器，在其他因素一定时，油液粘度的减小会导致液压变压器的变压比增大。其物理原因在于:粘度减小使得粘性摩擦转矩减小，从而引起变压比升高。

4)液压变压器变压过程中存在一个最大变压比点，而且液压变压器的输出流量越大，最大变压比点出现越早。

本文研究成果对液压变压器本体结构设计、变压比控制策略研究以及工程应用都具有重要的指导意义。

References)

［1］ van MALSEN R A H，ACHTEN P A J，VAEL G E M.Design of dynamic and efficient hydraulic systems around a simple hydraulic grid，SAE paper［R］.USA:SAE International，2002:1432 -1443.

［2］ VAEL G E M，ACHTEN P A J，FU Zhao.The innas hydraulic transformer-the key to the hydrostatic common pressure rail［R］.USA:SAE International，2000:2561 -2576.

［3］ 杨华勇，欧阳小平，徐兵.液压变压器的发展现状［J］.机械工程学报，2003，39(5):1 -5.YANG Hua-yong，OUYANG Xiao-ping，XU Bing.Development of hydraulic transformer［J］.Journal of Mechanical Engineering，2003，39(5):1 -5.(in Chinese)

［4］ ACHTEN P A J，FU Zhao，VAEL G E M.Transforming future hydraulics:a new design of a hydraulic transformer［C］∥Proc 5th Scandinavian International Conference on Fluid Power，SICFP’97.IKP:Linkoping University，1997:1 -23.

［5］ PETER P A J，van den BRINK T L，van den OEVER J，et al.Dedicated design of the hydraulic transformer［C］∥Proc 3rd International Fluid Power Conference.Aachen，Germany:2002:233 -248.

［6］ 欧阳小平.液压变压器研究［D］.杭州:浙江大学，2005.OUYANG Xiao-ping.Research on the hydraulic transformer［D］.Hangzhou:Zhejiang University，2005.(in Chinese)

［7］ 吕进中.斜轴式液压变压器变压特性与配流盘受力分析研究［D］.北京:北京理工大学，2008.LV Jin-zhong.Analysis of the characteristics of transformer ratio and of stress of valve plate about angle type hydraulic transformer［D］.Beijing:Beijing Institute of Technology，2008.(in Chinese)

［8］ 许铁军.斜轴式液压变压器变压技术研究［D］.北京:北京理工大学，2007.XU Tie-jun.Research on the transformer technology of angle type hydraulic transformer［D］.Beijing:Beijing Institute of Technology，2007.(in Chinese)