双领航多自主水下航行器移动长基线定位最优队形研究

房新鹏，严卫生

(西北工业大学 航海学院，陕西 西安710072)

0 引言

在多自主水下航行器(AUV)协作系统中，有效的任务规划和分配、避障处理和行为控制等群决策的实现都建立在高精度定位的前提上。因此需具备远距离、长时间、高精度的定位能力，以实现高度自主化和智能化，完成各项复杂任务。目前定位技术主要是声学定位系统，通常分为长基线定位系统、短基线定位系统与超短基线定位系统。长基线定位系统的精度最高，但AUV 的移动范围受限于应答器的布放区域，且布设、校准和回收作业的过程十分复杂［1］。针对这一问题，目前主要有3 种解决途径:1)挪威Kongsberg 公司利用水下应答器辅助AUV定位，并进行了DGPS、USBL、UTP、DVL 和INS 的综合定位导航技术的开发，由于无需母船支持，有效地拓展了AUV 作业范围，但尚未实际应用［2］;2)法国ACSA 公司开发了基于GPS 智能浮标的长基线水声定位技术，避免了海底应答器复杂的布放和校正过程，但仅能提供固定区域的导航定位服务［3］;3)美国MIT 提出了移动长基线(MLBL)定位新概念，利用时间同步信号和水声传播延迟进行相对位置测量［4］。

MLBL 定位最早由Vaganay 提出［4］，部分AUV装备高精度导航设备，其余AUV 装备低精度导航设备，利用声学距离量测进行位置更新。文献［5］介绍了WHOI 公司的水声调制解调器，可以实现AUV间时钟同步，精确测量水声信号传播时间，为MLBL定位系统的实现提供了技术支持。文献［6］介绍了基于极大似然法研究MLBL 定位系统。文献［7］利用无人水面船(USV)辅助AUV 进行了一系列MLBL 定位试验。为了降低定位系统复杂度，学者提出了单领航者定位系统。文献［8 -9］基于相对位移和航位推算信息研究了单领航者定位系统，文献［9］进一步研究了量测数据的选取和定位系统的观测性。文献［10］利用线性时变系统观测性理论分别研究了无洋流、已知洋流及未知洋流条件下单信标测距定位系统的观测性。文献［11］基于转移损耗函数极小化法研究了单领航者定位系统，并设计单USV 辅助AUV 定位的试验，取得了较好的定位效果。

当前，国内外关于AUV 水下定位系统的研究多集中在定位算法设计以及试验平台开发上，关于AUV 队形结构与定位性能关系的文献较少，文献［12］研究了队形结构对异构机器人定位精度的影响，设计了最优编队经验规则。针对这一问题，本文基于距离量测提出多AUV 移动长基线定位系统，利用Cramer-Rao 下界(CRLB)和Fisher 信息矩阵(FIM)理论建立与AUV 队形结构参数有关的定位性能评价函数，通过评价函数极大化实现定位性能最优化，在不提高传感器配置前提下进一步优化定位系统的定位性能。重点研究了双领航者定位系统的最优队形，并基于EKF 设计对比实验验证AUV间的距离值与分离角对定位性能的影响。

1 多AUV 移动长基线定位系统

1.1 移动长基线定位

移动长基线定位是近年来随着水声通信技术的进步而发展起来的一种定位技术。通过将应答器布设在USV 或者大型AUV 上，充当可移动的长基线定位基阵，利用AUV 之间的探测或通信确定被定位AUV 的位置，极大地降低了安装复杂性，拓展了应用范围。多AUV 移动长基线定位系统的原理如图1所示。

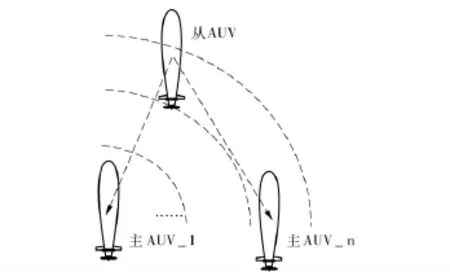
图1 多AUV 移动长基线定位系统原理图Fig.1 Cooperative localization based on MLBL of multi-AUVs

其中，领航AUV 可以利用自身携带的高精度惯性导航设备精确定位，而从AUV 仅装备低精度航位推算导航设备，需要通过协同方式进行定位，同时，二者外部均装备水声通信装置测量相对位置关系。从AUV 利用领航AUV 声信号脉冲传播时间解算二者间的相对距离，融合领航AUV 位置广播信息实现位置解算。

1.2 系统模型

航行过程中，AUV 的深度值可以由压力传感器直接测得，而且稳态运动时AUV 的俯仰角θ 较小，视作cosθ≈1.因此，可不考虑深度项，减小递推状态的维数，将AUV 在水下的三维定位问题简化为二维平面内的定位问题。本文假设领航AUV 与从AUV 均在同一深度平面内运动。

定义k 时刻从AUV 的平面运动状态为Xk=(xkykψk)T，其中，xk和yk表示k 时刻从AUV 在笛卡尔坐标系中的惯性坐标，ψk表示k 时刻从AUV的偏航角。建立采样周期为T 的从AUV 二维离散运动学模型为

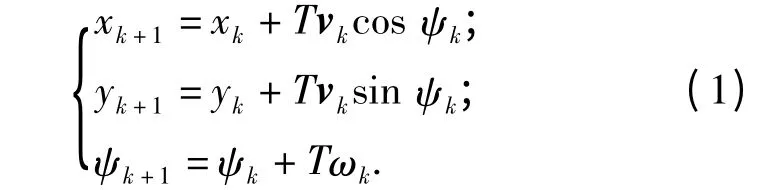
式中vk和ωk分别为k 时刻从AUV 的前向速度和偏航角速度，均受到高斯白噪声干扰，且噪声协方差

从而，AUV 的二维运动学方程可简写为

式中uk=(vkωk)T为k 时刻系统的控制输入。

建立从AUV 相对于第i(i =1…n)个领航AUV的距离量测方程:

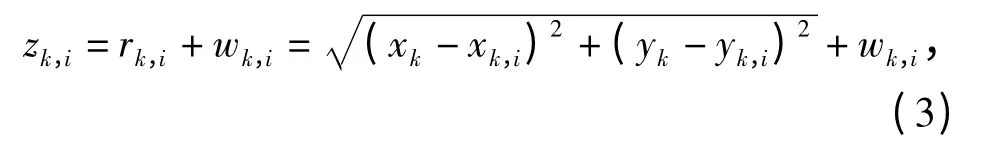
式中:rk，i为k 时刻从AUV 与第i 个领航AUV 之间的真实距离值;(xk，i，yk，i)T为第i(i =1…n)个领航AUV 在笛卡尔坐标系中的惯性坐标;wk，i为k 时刻的量测噪声。

试验证明，距离测量值误差仅仅弱相关于距离值，因此，假定k 时刻wk，i(i =1…n)为独立不相关的距离量测高斯白噪声，且其协方差为一个固定值［13］，即

式中wk=［wk，1… wk，n］T.

此时，距离量测方程(3)式的雅可比矩阵为

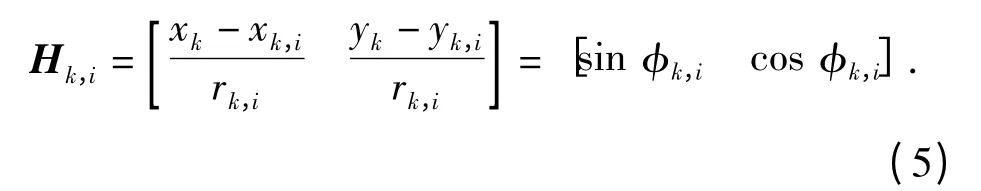
式中φk，i为k 时刻第i 个领航AUV 相对于从AUV的方位角，量测时选取顺时针方向为正，如图2所示。图中γij为第i、j 个领航AUV 与从AUV 间的分离角，γij=γji∈［0，π］.

图2 主从AUV 间相对结构示意图Fig.2 Relative geometry between leader AUVs and the follower

此处，从AUV 的系统状态只包括位置坐标(xk，yk)T，而没有考虑其偏航角ψk，这是因为在量测方程(3)式下偏航角参数不影响其位置误差，大大简化了系统模型。

2 双领航者定位系统最优队形

2.1 定位性能评价函数

定位过程实际上是一个状态预测过程，常用预测误差协方差来评价定位性能的优劣。克兰姆-罗不等式下界(CRLB)给出了未知参数无偏预测的协方差矩阵理论下界。因此，可以用CRLB 表征AUV队形对定位性能的影响。假设从AUV 位置状态xk的无偏估计为，则预测过程的CRLB 为

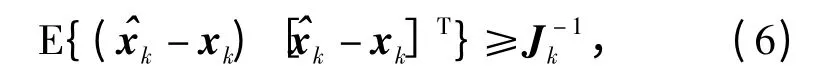
式中Jk为k 时刻的FIM，FIM 描述了预测过程中测量值所包含的状态变量信息量的大小。

预测过程中CRLB 值增大等同于FIM 值减小，也就意味着提高了预测性能，降低了预测不确定性。

k+1 时刻系统(2)式的FIM 可以写为如下递归计算形式［14］:

式中:Φk=xk-1f(Xk-1，uk-1);Rk，i和Hk，i的定义分别如(4)式～(5)式所示。

由于(7)式中没有从AUV 位置坐标的先验分布信息，Jk-1→∞，即→0.因此，可以将定位系统的FIM 简写为

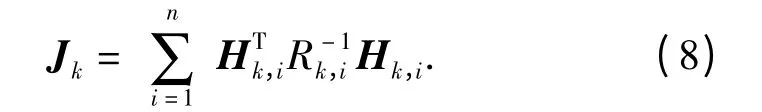
将Hk，i和Rk，i表达式代入(8)式，得到多AUV移动长基线定位系统FIM 为

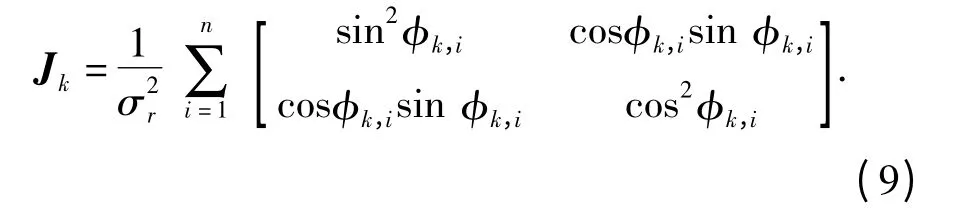
由于Jk是一个矩阵，很难通过最大化Jk解算最优队形，因此，考虑用一个基于(9)式的实值标量函数替代作为评价函数。综合计算量和评价效果等因素，选择FIM 的行列式(又称为D-最优准则)作为评价标准［15］。

计算(9)式的行列式，得到多AUV 移动长基线定位系统定位性能评价函数为

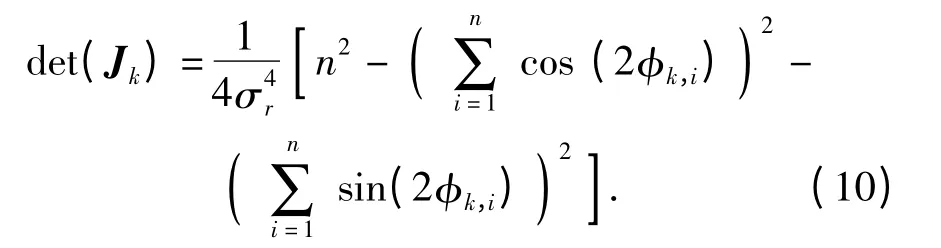
2.2 定位系统最优队形

由(10)式知，当n=1 时，det (Jk)≡0，因此，仅利用单一时刻AUV 间的距离量测无法实现从AUV位置状态的无偏估计。一般地，设计仅基于距离量测的多AUV 移动长基线定位系统时，至少需要n≥2 个领航AUV.文中多AUV 移动长基线定位系统选用两个领航AUV，即n=2.

当n=2 时，

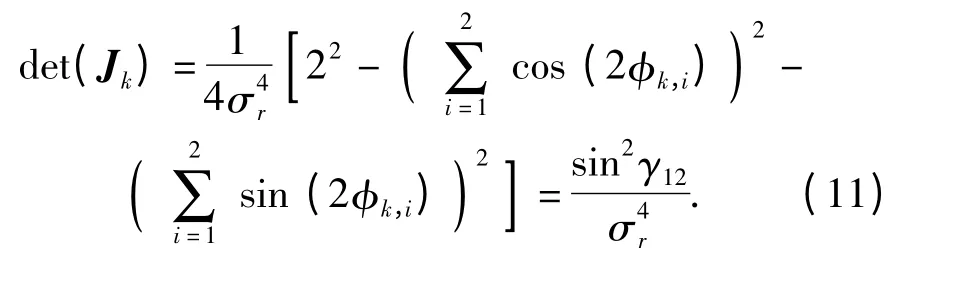
两个领航AUV 分别静止位于(-0.5 m，0)和(0.5 m，0)处，从AUV 在xk∈(-1.5 m，1.5 m)，yk∈(-1.5 m，1.5 m)区域运动，令σ2r=1，作双领航者移动长基线定位系统定位性能评价函数的三维网格图，如图3所示，图4为相应的等高线图。

由图3、图4知，从AUV 位置坐标在以(-0.5 m，0)和(0.5 m，0)为直径端点的圆的圆周上时，评价函数取得最大值，此时定位性能最优。

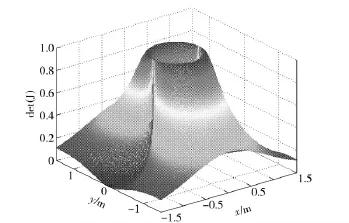
图3 评价函数三维网格图Fig.3 Three-dimensional mesh graph of evaluation function

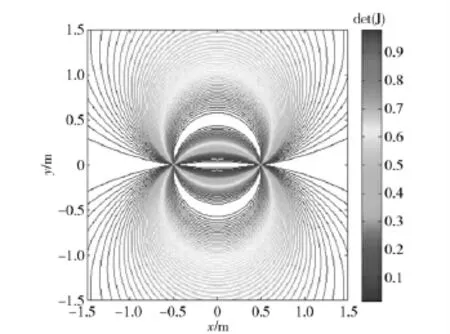
图4 评价函数等高线图Fig.4 The contour graph of evaluation function

综上所述，双领航者移动长基线定位系统最优队形为，两个领航AUV 与从AUV 保持90°分离角相对运动，且此最优队形与AUV 间的距离无关(实际操作中，为了避免AUV 之间发生碰撞等危险，需要设定AUV 间的最小允许安全距离)。

3 仿真分析

基于EKF 算法对基于双领航AUV 的移动长基线定位系统进行仿真实验，验证最优队形与分离角和间距之间的关系。实验设计中，假设AUV 之间最小安全距离为80 m，从AUV 距离量测方程高斯白噪声协方差σ2r=(10 m)2.采用蒙特卡洛法计算定位系统的定位误差，重复仿真计算100 次，取其统计平均值。

从AUV 从(20 m，20 m)处出发，以3 节的速度沿直线运动，偏航角为45°，两个领航AUV 分别从(100 m，20 m)和(20 m，100 m)处出发，以相同的速度和偏航角沿直线运动。领航AUV 与从AUV 之间的距离为80 m，分离角为90°，此时定位系统的运动队形最优。

在以上最优队形基础上改变两个领航AUV 的初始位置，使AUV 队形发生变化，验证分离角和间距的改变对定位性能的影响。

1)改变两个领航AUV 的初始位置分别为(100 m，20 m)和(89.3 m，30 m)，速度与偏航角不变。与改变前的最优队形相比，间距仍为80 m，只是分离角减小到30°。通过分析知，此时AUV 队形为非最优队形;

2)改变两个领航AUV 的初始位置分别为(160 m，20 m)和(20 m，160 m)，速度与偏航角不变。与改变前的最优队形相比，分离角仍为90°，只是间距增大到120 m.通过分析知，此时AUV 队形仍为最优队形。

图5和图6分别给出了队形改变前后定位系统平均定位误差的对比。由图5知，保持领航AUV 与从AUV 的间距为80 m 时，最优队形定位系统平均定位误差为3.037 m，非最优队形定位系统平均定位误差为4.312 m，最优队形提高定位精度约29.6%。由图6知，保持领航AUV 与从AUV 间的分离角为90°时，两种最优队形定位系统平均定位误差分别为3.032 m 和2.826 m，二者相差很小，间距对定位性能的影响并不明显。

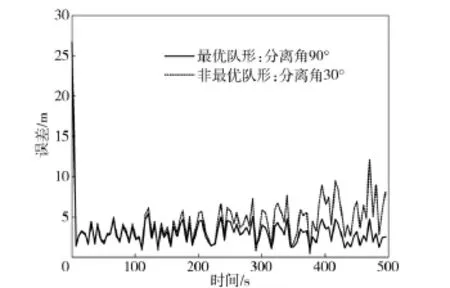
图5 变分离角定位系统平均定位误差Fig.5 The average localization errors with different separation angles

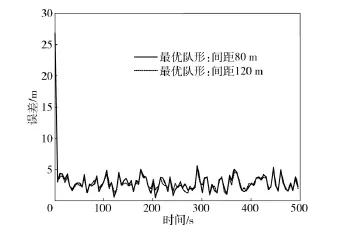
图6 变间距定位系统平均定位误差Fig.6 The average localization errors with different range

仿真实验进一步验证了最优队形受分离角的影响较大，而与间距无关。

4 结论

本文从CRLB 和FIM 的角度研究了双领航AUV 移动长基线定位系统。建立了定位性能评价函数，并通过评价函数极大化得到双领航者移动长基线定位系统的最优队形。仿真实验表明，保持分离角为90°基础上改变领航AUV 与从AUV 间的距离，对定位性能的影响很小，而保持间距为80 m 基础上改变领航AUV 与从AUV 间的分离角，则能显著影响定位性能。

References)

［1］ Stutters L，Liu H H，Tiltman C，et al.Navigation technologies for autonomous underwater vehicles［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part C:Applications and Reviews，2008，38(4):581 -589.

［2］ Jalving B，Gade K，Svartveit K，et al.DVL velocity aiding in the HUGIN 1000 intergrated inertial navigation system［J］.Modeling，Identification and Control，2004，24(4):223 -236.

［3］ Thomas H G.GIB buoys:an interface between space and depths of the oceans［C］∥Proceedings of The 1998 Workshop on Autonomous Underwater Vehicles，Cambridge:IEEE，1998:181 -184.

［4］ Leonard J J，Curcio J A，Willcox J S.Experimental validation of the moving long base-line navigation concept［C］∥Proceedings of 2004 IEEE/OES Autonomous Underwater Vehicles.Cambridge:IEEE，2004:59 -65.

［5］ Freitag L，Johnson M，Grund M，et al.Integrated acoustic communication and navigation for multiple UUVs［C］∥Proceedings of MTS/IEEE Oceans 2001 Conference and Exhibition.Honolulu:IEEE，2001:2065 -2070.

［6］ Eustice R M，Whitcomb L L，Singh H，et al.Recent advances in synchronous-clock one-way-travel-time acoustic navigation［C］∥Proceedings of the IEEE/MTS Oceans 2006 Conference and Exhibition.Boston:IEEE，2006:1 -6.

［7］ Curcio J，Leonard J，Vaganay J，et al.Experiments in moving baseline navigation using autonomous surface craft［C］∥Proceedings of the IEEE/MTS Oceans 2005 Conference and Exhibition.Washnigon DC:IEEE，2005:730 -735.

［8］ 张立川，刘明雍，徐德民，等.基于水声传播延迟的主从式多无人水下航行器协同导航定位研究［J］.兵工学报，2009，30(12):1674 -1678.ZHANG Li-chuan，LIU Ming-yong，XU De-min，et al.Cooperative localization for multi-UUVs based on time-of-flight of acoustic signal［J］.Acta Armamentarii，2009，30(12):1674 -1678.(in Chinese)

［9］ 李闻白，刘明雍，张立川，等.单领航者相对位移测量的多自主水下航行器协同导航［J］.兵工学报，2011，32(8):1002 -1007.LI Wen-bai，LIU Ming-yong，ZHANG Li-chuan，et al.Cooperative navigation for multiple autonomous underwater vehicles based on relative displacement measurement with a single leader［J］.Acta Armamentarii，2011，32(8):1002 -1007.(in Chinese)

［10］ Gadre A S.Observability analysis in navigation systems with an underwater vehicle application［D］.Virginia:Virginia Polytechnic Institute and State University，2007:39 -42，53 -56.

［11］ Papadopoulos G，Fallon M F，Leonard J J，et al.Cooperative localization of marine vehicles using nonlinear state estimation［C］∥Proceedings of 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems.Taipei:IEEE，2010:4874 -4879.

［12］ Yukikazu S H，Anastasios I M，Stergios I R.Optimal formation for cooperative localization of mobile robots［C］∥Proceedings of 2005 IEEE International Conference on Robotics and Automation.Barcelona:IEEE，2005:4137 -4142.

［13］ Bahr A，Leonard J J，Fallon M F.Cooperative localization for autonomous underwater vehicles［J］.The International Journal of Robotics Research，2009，28(6):714 -728.

［14］ Hernandez M L.Optimal sensor trajectories in bearings-only tracking［C］∥Proceedings of the Seventh International Conference on Information Fusion.Stockholm:Internation Society of Information Fusion，2004:893 -900.

［15］ Sameera S P，Richard M K，Emilio F.Trajectory optimization for target localization using small unmanned aerial vehicles［C］∥Proceedings of AIAA Conference on Guidance，Navigation，and Control.Chicago:AIAA，2009:1211 -1235.