基于考虑外生变量的SWARCH模型对中国股市波动性的实证研究
李金凤, 张德生, 井霞霞
(西安理工大学理学院, 陕西 西安 710054)
0 引 言
金融时间序列的波动性是金融研究中的一个热门课题,波动带来风险,实际生活中几乎所有的金融序列都具有波动性,因此,通过描述波动来控制风险仍是当前研究的热点.在股票市场,股票的正常波动使资本市场活跃,但过于频繁的波动却会增加市场风险,影响投资判断.
研究发现金融数据,尤其是股票数据,收益率序列数据的方差经常随时间变化,而且呈尖峰厚尾分布.从1982年Engle[1]提出了ARCH(q)模型一直到现在,人们对ARCH模型的改进不断在进行,出现了GARCH类模型等,这些模型对股票的波动性有很好的刻画,但也有不足,为此,Hamilton和Susmel[2](1994)结合Markov状态转移和ARCH模型提出了SWARCH模型,并验证了SWARCH模型较传统的GARCH类模型更能刻画股票的波动.国内学者利用 SWARCH 模型进行实证研究是从21世纪开始的.蒋祥林等(2004)[3]应用SWARCH 模型对我股市的波动性进行了分析;苏涛等(2005)[4]将SWARCH 引入到估计金融资产VaR 中;丁志国(2007)[5]基于向量SWARCH 模型,实证检验了我国GDP 增长率与证券收益率间的关联性.股市的波动受到很多因素的影响,如将影响因素直接加入到波动方程对股票的波动进行研究应该会有很好的效果,本文将就这一问题进行实证研究.
1 具有外生变量的SWARCH(SWARCHX)模型
用yt表示市场指数的收益率,Hamilton和Susmel(1994)[2]建立了如下模型
yt=φ0+φ1yt-1+…+φpyt-p+et
(1)
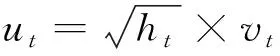
(2)
(3)
(4)
这里,vt-1为货币供应量,即本文所要考虑的外生变量;当δ=0时,该模型就为SWARCH模型,当δ≠0时就是本文要用的SWARCHX模型.st表示一个不可观测的区制变量,其可能取值为1,2,…,k,并假设其服从一阶Markov链过程:
p(st=j|st-1=i,st-2=k,…,yt-1,yt-2,…)=p(st=j|st-1=i)=pij
(5)
转移概率矩阵为:
(6)
矩阵中每一列各元素之和为1.
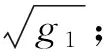
2 实证分析
2.1 数据分析处理
本文选取1996年1月至2011年5月的上证指数月度数据和货币供应量,共185个数据,用前180个数据建立模型,后5个数据进行预测检验,数据来源于凤凰财经网(http://app.finance.ifeng.com/data/).
在建立模型之前,先应用Eviews软件对数据进行相应的统计检验,结果如图1.

图1 原始数据的描述性统计特征

2.2 模型建立
本文借鉴文献[6]的研究结果——两区制的SWARCH模型对上证指数月度数据的描述更确切,建立两区制的SWARCH模型,利用GUASS软件编程得到表1所示参数的准确估计结果.
考虑外生变量的SWARCH(SWARCHX)模型表达式为:
其中,vt服从单位方差,自由度为10.896 7的t分布.
其转移矩阵为:
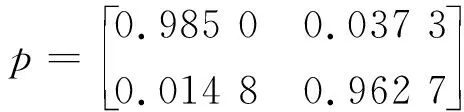
从表1可知外生变量显著,且模型达到稳定状态,说明模型建立合理.
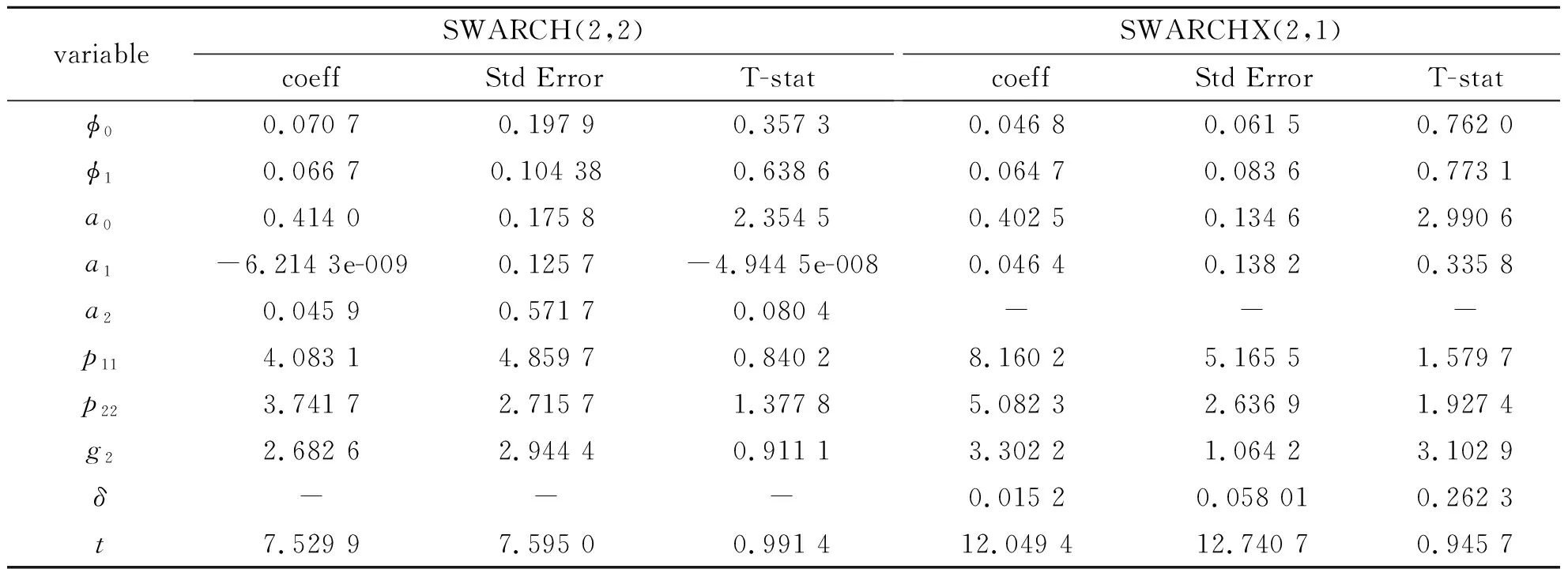
表1 系数估计结果
2.3 拟合效果对比
下面检验考虑外生变量的SWARCH模型是否对SWARCH模型有所改进,首先给出各模型估计结果比较,如表2所示.

表2 不同模型估计结果
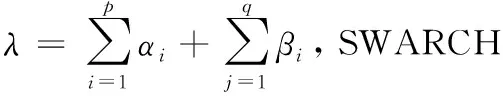
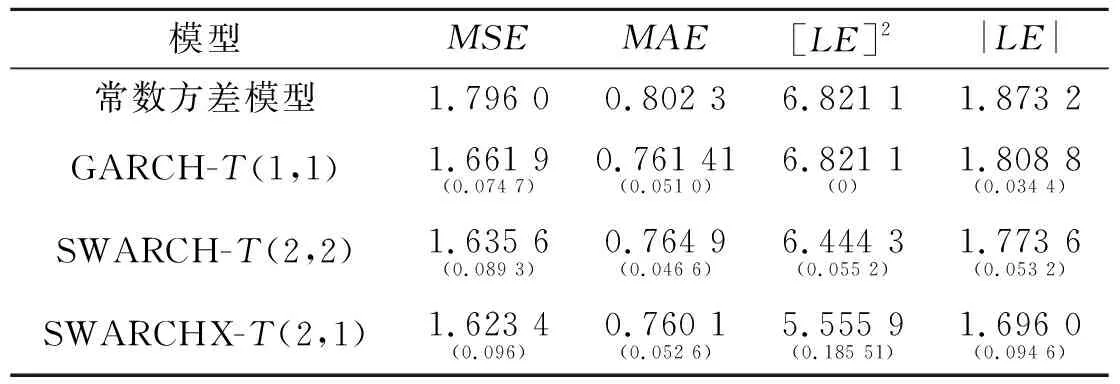
表3 数据波动样本内拟合结果对比

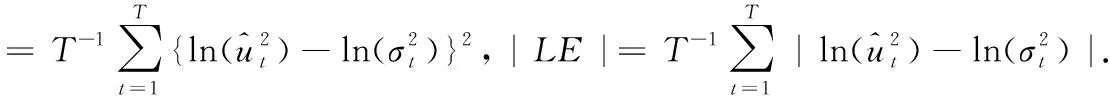
表2给出了不同模型估计结果比较,基于AIC、SC准则比较分析得出,SWARCH模型较GARCH模型更好的描述了收益率序列的特征;而SWARCHX模型较SWARCH模型的效果在这方面也有很好的提高,说明SWARCHX模型能更好的描述上证指数的特征.在持续性上可以很明显的看到,SWARCH模型较GARCH模型持续性明显降低,说明SWARCH模型很好的解决了GARCH模型在预测上的高持续性,而SWARCHX模型更是降低了冲击的持续性,相对于月的数据来说,低的持续性更适合用来描述序列的特征.
从表3知,加入外生变量的SWARCH模型(SWARCHX)在拟合效果上不仅比传统的GARCH类模型有很好的均方误差,更重要的是比不加入外生变量的SWARCH模型在均方误差方面有所改进.即便是按误差均值最小化标准来看,SWARCHX模型比不加入外生变量的SWARCH模型也有所改善,是本文所研究模型中最好的,从其他两个评价标准来看SWARCHX模型也是最合适的,所以,SWARCHX模型较SWARCH模型在各个方面都有所提高.
2.3.1 波动性描述
从图2知,3个模型所估计的波动性的走势是一致的,但GARCH类模型和SWARCH类模型最大的差别在于对一些大的事件冲击所作出的反应不同. GARCH模型以极慢的回复速度对大的事件冲击作出反应,而 SWARCH类模型能以极高的速度回归到与某一特定波动性状态相联系的趋势水平.SWARCH类模型预测性能的提高是由于其不需要对冲击强加上高的持续性效应就能够跟踪波动性的长期变动趋势,SWARCH类模型将波动性的持续性分解为波动性状态的持续性和某一波动性状态下波动性冲击的持续性,这样就更好地描述了波动性的特征.从第二行的两个图比较可以看出,SWARCHX模型表现出对冲击的反应更灵敏,更快速,不论是在初期,还是后来的低波动期和高波动期都比不考虑外生变量的SWARCH模型恢复速度快,即较低的持续性,这一点从表2所列的持续性参数就可以得到更确切的答案.
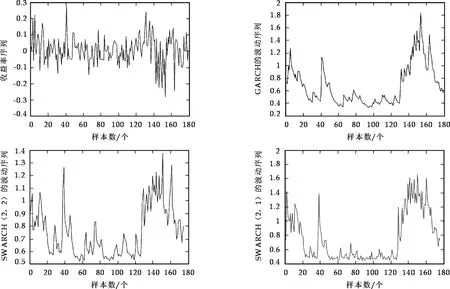
图2 基于不同模型的波动性估计结果的比较

模型MSEMAE[LE]2|LE|GARCH-T(1,1)0.095 90.060 8-0.062 40.002 9SWARCH-T(2,2)0.116 30.054 60.128 90.056 2SWARCHX-T(2,1)0.120 90.068 30.106 90.065 9
注:数值为相应模型相对于常数方差模型预测能力的提高比例,其值越大越好.
2.3.2 波动预测结果对比
建立模型对股票波动进行研究,更关注的是对未来情况的预测,表4给出了SWARCHX模型在预测方面的效果.
从表4可以看出,SWARCH类模型对波动的预测能力相对于GARCH类模型有显著的提高,说明SWARCH模型较好的解决了GARCH类模型在高持续性的波动和波动预测能力之间不协调的矛盾.同时可见,加入外生变量的SWARCH模型相对于不考虑外生变量的SWARCH模型在预测能力上也有所提高.
3 结束语
本文考虑了股票市场的波动受货币供应量的影响,对上证指数考虑外生变量的SWARCH模型进行了研究,实证研究结果表明:考虑外生变量的SWARCH模型在对股票市场波动性的拟合和预测方面都有所改进.
参考文献
[1] Engel R F.Autoregressive conditional hetero skedasticity with estimates of the variance of U K[C].Inflation Econometrics,1982:987-1 008.
[2] Hamilton J D, Susmel R. Autoregressive conditional heteroskedasticity and changes in regime[J]. Journal of Econometrics,1994,(64):307-333.
[3] 蒋祥林,王春峰,吴晓霖. 基于状态转移ARCH模型的中国股市波动性研究[J].系统工程学报,2004,(3):270-277.
[4] 苏 涛,詹原瑞. SWARCH模型下的VaR 估计[J].数量经济技术经济研究,2005,(12):143-149.
[5] 丁志国,苏 治,杜晓宇. 经济周期与证券市场波动关联性-基于向量SWARCH模型的新证据[J].数量经济技术经济研究,2007,(3):61-69.
[6] 王 晨. 我国金融市场波动的区制关联性与风险度量研究[D]. 长春:吉林大学硕士学位论文,2010.
——基于MS-VAR模型

