一种改进的蒙特卡罗定位算法研究
邵清亮,李玉峰,屈乐乐,王 鹏
(1.沈阳航空航天大学 沈阳110136;2.东软飞利浦医疗设备系统有限责任公司 沈阳110179)
1 引言
在无线传感器网络的许多应用中,节点位置至关重要,离开位置信息,监测事件或者感知数据也失去了实际应用价值。若仅为每个传感器节点均配置GPS收发器,其成本和能耗较高,不符合无线传感器网络各方面的约束,若没有位置信息,传感器节点所采集的数据几乎是没有应用价值的。因此,在无线传感器网络的应用中,节点定位成为关键的问题。
目前,节点的定位方法主要有基于测距(range-based)的定位和无须测距(range-free)的定位两种。测距方法利用接收信号强度指示(RSSI)、信号到达时间(TOA)[1],不同信号到达的时间差分(TDOA)[2]以及到达角度(AOA)[3]等测量相邻节点的距离。非测距定位算法则不需要距离和角度信息,算法根据网络连通性等信息来实 现 节 点 定 位,如 质 心 算 法、DV-Hop、Amorphous、MDS-MAP和APIT算 法 等[4~6],在以上的算法中没有很好的能够针对移动节点的定位,传统的蒙特卡罗方法能够较好地解决移动节点定位,但其估计误差较大,而且在采样的过程中,为了避免粒子退化,计算量非常大,造成传感器节点能量的大量消耗。
本文提出了一种基于接收信号强度的蒙特卡罗算法,缩小了传统蒙特卡罗算法采样的范围,降低了重复采样率以及节点的能量消耗。
2 RSS测量模型
测量节点的RSS[7]是一种指示当前介质中电磁波能量大小的数值。RSS值随距离增加而减小,锚节点可以通过RSS值计算出未知节点与它的距离。虽然传感器节点自身具备通信能力,借助的硬件设备较少,相对其他测距技术而言是一种低功率、廉价的测距技术,但是无线电传播过程中由于多径、绕射、障碍物等因素对RSS定位算法的定位精度有很大影响[8],所以单独使用RSS方法很难对节点进行较精确的定位。
在实际应用中,无线电传播路径损耗模型十分复杂,由于阴影效应的随机特性,接收功率的测量值不同于计算得到的平均接收功率,测量值与平均值之间的差可以由对数正态分布来描述,因而传感器i所接收到的来自传感器j的接收功率Pij(dBm)是遵循高斯分布的一个随机变量[9],这里是传感器i所接收到的总的平均接收功率(dBm),δdB是阴影衰落标准差(dB),它是关于距离的一个常量。设P0表示在参考距离d0时的接收功率(dBm),假设传感器j的发射功率Pt(dBm),P0可依据自由空间环境下路径损耗条件计算得到P0=Pt-20lg(4πd0λ),其中λ是信号载波的波长。根据上式,接收功率的期望值依赖于传感器节点i的位置mi=(xi,yi),用dij表示发射点(xi,yi)和接收点(xj,yj)之间的欧几里德几何距离,因而,传感器i在位置mi具有接收功率P的条件概率为:

式(1)给出了节点i在位置mi的接收功率。
假设在时刻k时某未知节点有L个邻居锚节点,通常得到的L×1的测量向量nk与未知节点的位置mk是相互独立的。在不同时刻,对不同的未知节点,其邻居锚节点的数量可能不同。因而,重新改写式(1)得到:

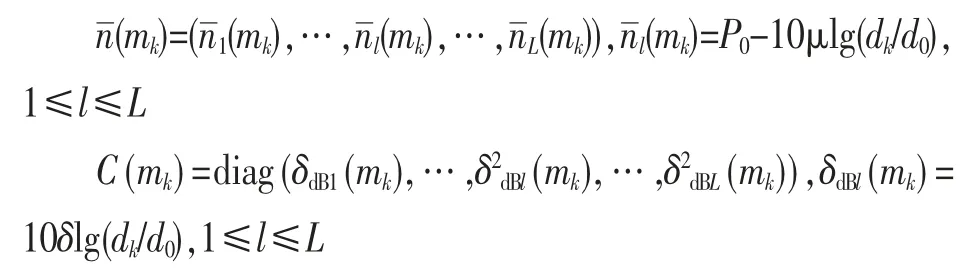
3 基于RSS的MCL方法
蒙塔卡罗定位MCL算法是一种无须测距的分布式算法,相对于其他算法而言有着较大的优势,但是在参考文献[10]中指出MCL仍存在不足,主要体现在:采样区域很大,导致采样的效率过低,同时也降低了定位精度。若MCL算法在以每个样本点为圆心、最大移动速度为半径的圆内随机采样,这样会导致很多采样点不符合过滤条件,在过滤阶段被过滤掉。为了取得足够的样本数,抽样过程需要不断重复,抽样次数大大增加,有时甚至达到设置的最大抽样次数后,还抽不到足够的样本,导致抽样失败,降低了定位效率和定位精度,采用改进的蒙特卡罗算法可以提高采样率,缩短采样时间。
3.1 位置预测
假设有一传感器网络,其中有N个未知节点和M个锚节点,锚节点的位置已知。未知节点处于移动状态,并且彼此之间的移动相互独立,基于传感器节点的移动特性和RSS测量模型,用mk~P(mk|mk-1),k≥0表示给定节点在前一时刻的位置为mk-1时,当前时刻在mk的概率,该方程称为转移方程。用nk~P(nk|nk-1),k≥0描述在给定位置时对RSS测量的似然度,该方程成为观测方程。
若未知节点随机地从最大速度vmax和最小速度vmin之间选取一个值进行移动,其移动方向随机地从[0,2π]选出,则给定未知节点在前一时刻的位置,其当前时刻位置估计的概率,即转移分布P(mk|mk-1),形成一个以mk-1为圆心、内半径为vmin、外半径vmax的圆环,如下:
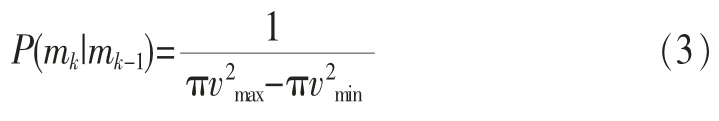
式(3)表示了在前一时刻的位置mk-1时,当前位置的分布情况。在蒙特卡罗算法预测阶段,基于前一时刻的位置估计,节点在任意时刻可能的位置即可从该圆中随机地采样,称该圆形区域为采样区域。由于并不知道未知节点的移动速度和移动方向,其位置的随机采样增加了不确定性,因而需要通过从RSS的观测信息中采样来减小其不确定性。
3.2 位置更新
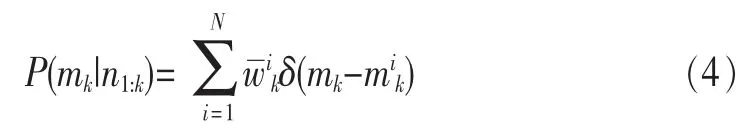

通过节点位置预测和权重值更新的反复计算,可得到后验分布p(mk|n1:k)。
3.3 重采样
在以上的计算过程中,若经过多次迭代后,所有归一化的权重值除其中的一个,其余的均非常接近于0。由于重要性权重的方差随着时间的推移而增长,退化现象无法避免[11]。退化现象意味着大量的计算资源花在了那些对后验分布估计贡献很小的粒子上面。因而,在采用重采样时结合RSS值,提高采样的有效性,同时设定有效样本数量为一固定阈值,低于此值则开始启动重采样。
4 仿真与分析
构建一个500 m×500 m的具有N个未知节点和M个锚节点的无线传感器网络。未知节点随机地分布于网络中,并且其移动特性遵循随机移动模型,其移动速度从l m/s(vmin)到20 m/s(vmax)中选择,移动方向未知,同时锚节点假定处于静止状态。
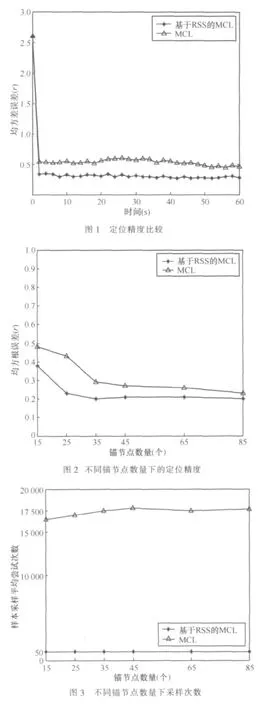
假定未知节点和锚节点的通信半径r均为100 m,样本数量设为50个,锚节点设为25个。通过仿真对比,从图1中可以看出,在单位时间内,基于RSS的MCL方法比传统MCL方法的定位精度高。
大多数基于锚节点的定位算法,定位精度通常受锚节点数量的影响。随着锚节点数量的增加,定位精度也增加,较高的锚节点密度可以产生较高的定位精度,但当锚节点数量到达一定数量,如图2所示,达到80个时,定位精度改善非常小。仿真表明,数量一定的锚节点情况下,基于RSS的MCL的定位精度比非测距的MCL定位精度要高。
由于蒙特卡罗定位算法多数的处理时间消耗在采样过程中,这里对不同锚节点和未知节点数量下的采样过程进行仿真,如图3所示。从图3可以看出,非测距MCL要花费大量的采样尝试次数才能采集到符合要求的样本,对任何数量的锚节点,该算法大概需要采样17 500次,这是由于从采样区域中采集的样本并不都是有效的,因而增加了重复采样次数。而基于RSS的MCL方法仅需要50次采样,就能够完成有效采样。从仿真结果可以看出,基于RSS的MCL方法需要的计算代价远小于MCL方法。
将节点位置在每次定位过程中所发送的消息作为定位通信开销。由于未知节点的两跳邻居锚节点的发现需要未知节点发送较多的消息,所以MCL方法比基于RSS的MCL需要更多的开销,仿真结果如图4所示。从图4可以看出,未知节点一定的锚节点变化的情况下,MCL方法比基于RSS的MCL方法多发送11个消息。

5 结束语
无线传感器网络的移动节点定位方法中,传统的蒙特卡罗算法的重采样增大了节点的计算量,增加了传感器节点能量消耗,本文在测得RSS值的基础上,利用MCL方法降低节点计算量,仿真表明,在锚节点和未知节点数量一定的情况下,基于RSS的MCL改进算法的定位精度高于传统的MCL方法,而且改进的算法样本采样次数少、通信开销小,对降低无线传感器网络能耗有着积极作用。
1 Harter A,Hopper A,Steggles P,et al.The anatomy of a con-textaware application.MobiCom,Seattle,Washington,USA,1999
2 Girod L,Estrin D.Robust range estimation using acoustic and multimodal sensing.Proceedings of the IEEE/RSJ Int'l Conf on Intelligent Robots and Systems(IROS 01),Maui,Hawaii,USA,2001
3 Niculescu D,Nath B.Ad Hoc positioning system(APS)using AOA.IEEE INFOCOM,San Francisco California,USA,2003
4 Niculescu D,Nath B.Ad Hoc positioning systems(APS).Proceedings of the 2001 IEEE Global Telecommunications Conference,IEEE Communications Society,2001
5 Niculescu D,Nath B.DV based positioning in Ad Hoc networks.Journal of Telecommunication Systems,2003,22(1):267~280
6 Bahl P,Padmanabhan V N.RADAR:an in-building RF-based user location and tracking system.Proceedings of the 19th Annual Joint Conference on IEEE Computer and Communications Societies,Aviv,Israel:IEEE Press,2000
7 Girod L,Bychovskiy V,Elson J,et al.Locating tiny sensors in time and space:a case study.IEEE ICCD,Freiburg,Germany,2002
8 Elnahrawy E,Li X,Martin R P.The limits of localization using signal strength:a comparative study.IEEE SECON,Santa Clara,CA,USA,2004
9 Neal Patwari,Nciycr S C,Robert J.Relative location estimation in wireless sensor network.IEEE Transaction on Signal Processing,2003,l51(8):2 137~2 148
10 Hu L,Evans D.Localization for mobile sensor networks.Proceedings of the 10th Annual International Conference on MobileComputingandNetworking,Philadelphia:ACMsociety,2004
11 Doucet A,Godsill S,Andrieu C.On sequential monte carlo sampling methods for bayesian filtering.Statistics and Computing,2000(10)

