改进的协同粒子群优化算法的研究与应用❋

陈如清, 杨 妍

(1.嘉兴学院机电工程学院 嘉兴,314001) (2.华东理工大学自动化研究所 上海,200237)

引 言

旋转机械的故障诊断对减少故障危害及增加设备安全性具有重要意义[1-2]。人工神经网络用于故障诊断,解决了多维空间模式或非线性模式的识别问题,适合于对多故障、多征兆等复杂对象进行故障诊断[3-4]。学习算法是神经网络研究的一项重要内容,其性能好坏直接影响到网络模型的性能,BP算法是前向神经网络广泛采用的学习方法。用于实际复杂故障建模时,BP神经网络存在结构复杂、收敛速度慢等不足,不利于完成实时性强的机械设备故障诊断。粒子群优化算法(particle swarm optimization,简称PSO)是基于群体的演化算法,其基本思想源于对鸟群捕食行为的研究。由于PSO算法原理简单易于实现,没有太多参数需要调整,且不需要梯度信息,目前已广泛用于神经网络训练、函数优化、模糊系统控制及其他遗传算法的应用领域。但PSO用于神经网络训练时也存在易陷入局部最优、进化后期收敛速度较慢、鲁棒性较差等不足。

笔者针对 BP和基本 PSO算法用于神经网络训练时存在的不足,基于现有算法提出了一种改进的协同粒子群优化算法(improved cooperative PSO,简称 ICPSO)。

1 改进的协同粒子群优化算法

1.1 算法原理

协同进化算法是对进化算法的一大改进[5]。为了克服 PSO算法的缺陷,提出了协同粒子群优化算法(cooperative PSO,简称 CPSO)[6]。 CPSO算法采用两层结构:底层用多个粒子群相互独立地搜索解空间以扩大搜索范围;上层用 1个粒子群追逐当前全局最优解以加快算法收敛。通过底层多个粒子群的独立搜索来保证寻优过程可以在较大范围内进行,同时利用上层粒子群追逐当前全局最优点保证算法收敛,兼顾了优化过程的精度和效率。CPSO是一个很有潜力的研究方向[7]。

CPSO使用方便,收敛速度较快,但操作要比PSO复杂。多粒子群协同优化是通过多个子粒子群对主粒子群的协同指导实现优化,主群与子群间采取何种协同策略是算法成功与否的关键。为进一步改善现有 PSO和 CPSO算法的优化性能,在原有方法基础上[8]提出了一种改进的 ICPSO方法。

如图 1所示,其基本原理为:整个粒子群体由m个子种群组成,各子种群均用标准 PSO算法搜索机制进化,更新群内粒子的速度和位置,相邻两个子种群周期性地进行信息交流。每当进化到第t=nT代时(T为更新周期,n为自然数),第i个子种群将其当前的群体最好解yi(t)传给第i+1个子种群(i=1,2,… ,m)。第i+ 1个子种群依据yi(t)和yi+1(t)的权平均值(即前一个子种群的群体最好解和本子种群的群体最好解的权平均值)进化,依次类推。最后一个子种群将其群体最好解ym(t)传回给第1个子种群。在每个nT更新周期,各子种群都将本分群的群体最好解传递给下一个相邻的子种群,同时判断yi(t)(i=1,2,… ,m)是否满足精度,若满足则停止,否则继续进化。

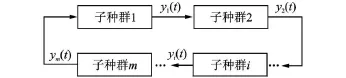
图1 ICPSO协同策略

迭代过程中,粒子(第i+ 1个子种群)根据如下公式来更新自己的速度和位置

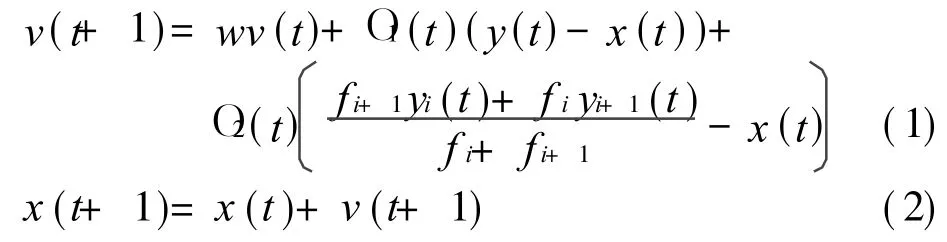
其中:O1(t)=c1r1(t);O2(t)=c2r2(t);c1和c2为加速因子;r1和r2为两个在[0,1]范围内变化的随机数;x(t),v(t)分别为t时刻粒子的位置和空间速度;y(t)为粒子历史最好解(个体极值点);w为惯性权值;fi为解yi对应的适应度值;fi+1为解yi+1对应的适应度值。

ICPSO算法在进化过程中,各子分群粒子能充分利用本分群搜索经验和整个种群搜索经验,既能确保在本子种群内部不断地搜索,不会迷失自己的寻优方向,又能周期性地共享整个种群最优值指导粒子找到最好解。此外,分解为多个子种群有利于维持种群的多样性,能有效抑制局部最优现象发生。

PSO算法产生的初期并没有对算法的收敛性进行详细分析,参数的选取主要依赖经验。一些学者[9]从数学的角度对算法的收敛性进行了分析。采用类似方法分析表明,笔者提出的 ICPSO算法的每个粒子最终收敛于一平衡点,即群体中粒子最终收敛于个体最优解和群体最优解的权平衡点。

1.2 ICPSO算法流程

算法流程为:

1)设定整群粒子规模N,子种群数量m,则子种群包含粒子数目为N/m,设置更新周期T。初始化各分群粒子的位置、最大迭代次数、优化精度及 PSO算法的相关初始参数,计算所有粒子的初始适应值并保存各分群最好适应值及相应位置。

2)迭代开始,在第1个迭代周期内 (第1～T次迭代过程),各分群粒子按基本 PSO搜索机制产生粒子新位置并计算新适应值,更新个体历史最好适应值及分群历史最好适应值。第j个迭代周期(其中j=2～n,n=最大迭代次数 /更新周期T)内,所有粒子完成前j-1个迭代周期的搜索。

3)各子种群接收与之相邻的上一个子种群的当前最好解,并将其传递给下一个子种群(如图1所示),各分群粒子根据式(1)和式(2)来更新自己的速度和新的位置。

4)同步骤2,各分群粒子按基本 PSO机制进行搜索,直至本周期结束。

5)记录各分群的历史最好适应值及对应粒子的空间位置。

6)令j=j+1,若满足停止条件(适应值误差达到设定的适应值误差限或迭代次数超过最大允许迭代次数),搜索停止,输出全群历史最优位置和最优适应值;否则,返回步骤3继续搜索。

2 仿真研究

为验证 ICPSO算法的有效性,模拟试验选取多峰值、存在许多局部最小点且自变量之间相互独立或互相影响的 4个经典函数(Rastrigrin,Griewank,Ackley和Rosenbrock函数)作为寻优测试对象。采用ICPSO算法和基本 PSO算法对其进行寻优测试。

用Matlab软件编写相关程序,两种算法在仿真过程中,函数维数、粒子规模、最大迭代次数和最大最小惯性权值等基本参数均设置相同。优化时用两算法对每一测试函数都进行 200次独立测试,ICPSO算法参数设计见表 1。

仿真结束后对测试结果进行统计分析。为全面比较算法性能,采用相对通用的指标评价来优化算法性能。笔者采用的评价指标包括:寻优率、平均精度、最大迭代次数和平均迭代次数[10]。统计结果见表2。

由表 2可知,在算法基本参数设置相同的情况下,ICPSO算法整体寻优性能明显优于基本 PSO算法。其中,Griewank,Rastrigrin和 Ackley函数在低维数情况下局部最优点就很多。随着维数的增高局部最优点的数量也迅速增加,增加了最优解的寻找难度。对这3个高维函数,基本PSO算法较易陷入局部最优,而改进算法能准确快速地找到全局最优解,算法的稳定性也较好。此外,多维Rosenbrock函数的最优解分布非常复杂,ICPSO算法表现也强于基本PSO算法。

综上所述,对几个复杂函数的寻优测试表明,改进的 ICPSO算法的收敛速度、收敛精度和全局搜索性能显著高于基本 PSO算法,与理论分析相符合。

表1 ICPSO算法参数设计

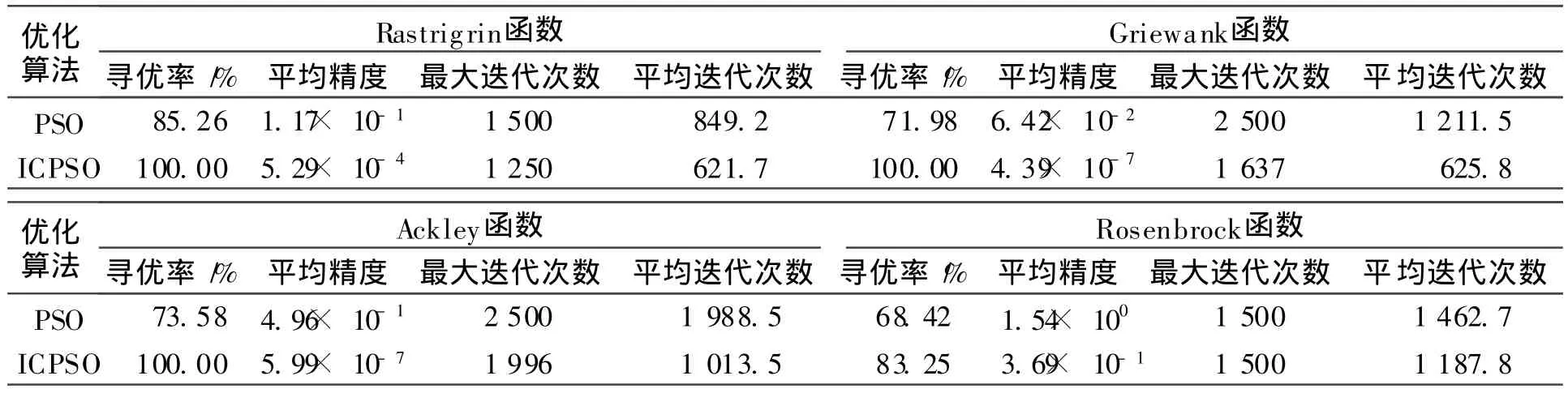
表2 两种寻优算法寻优性能对比(200次试验)

3 旋转机械故障诊断中的应用

3.1 故障建模及故障样本设计

某旋转机械构成部件主要有转子轴、定子、轴承座及叶轮等。常见的故障主要有转子不平衡、转子不对中、轴承座松动、摩擦故障等 10类故障。研究表明,旋转机械振动信号的频谱能较敏感地反映各种故障状态[1-4]。基于神经网络的故障诊断系统是用神经网络构建故障特征与故障状态之间的映射关系。

振动信号中含有丰富的故障信息,通过对其进行频谱分析可分离出振动信号的主要频率部分,得出各种振动频率的幅值。不同故障情况其频率分布及幅值大小各有不同,据此可推断故障原因。如转子不平衡故障其谱峰能量主要集中在f频段上(f为基频,A为振幅);转子不对中故障下谱峰能量主要集中在f,2f,3f频段上;其他故障也有类似征兆。故障分析时分别以频谱中 9个频段(0.01f～ 0.39f,0.40f～ 0.49f,0.50f,0.51f～ 0.99f,1f,2f,3f～ 5f,奇数次f,高频段)上的不同频率的谱峰能量值作为特征向量。这样以9维故障特征量作为神经网络的输入,输出为 10维故障编码,共有 10类故障样本。目标输出为“1”表示相应故障发生,为“0”则不发生。 10类典型故障样本如表 3所示。

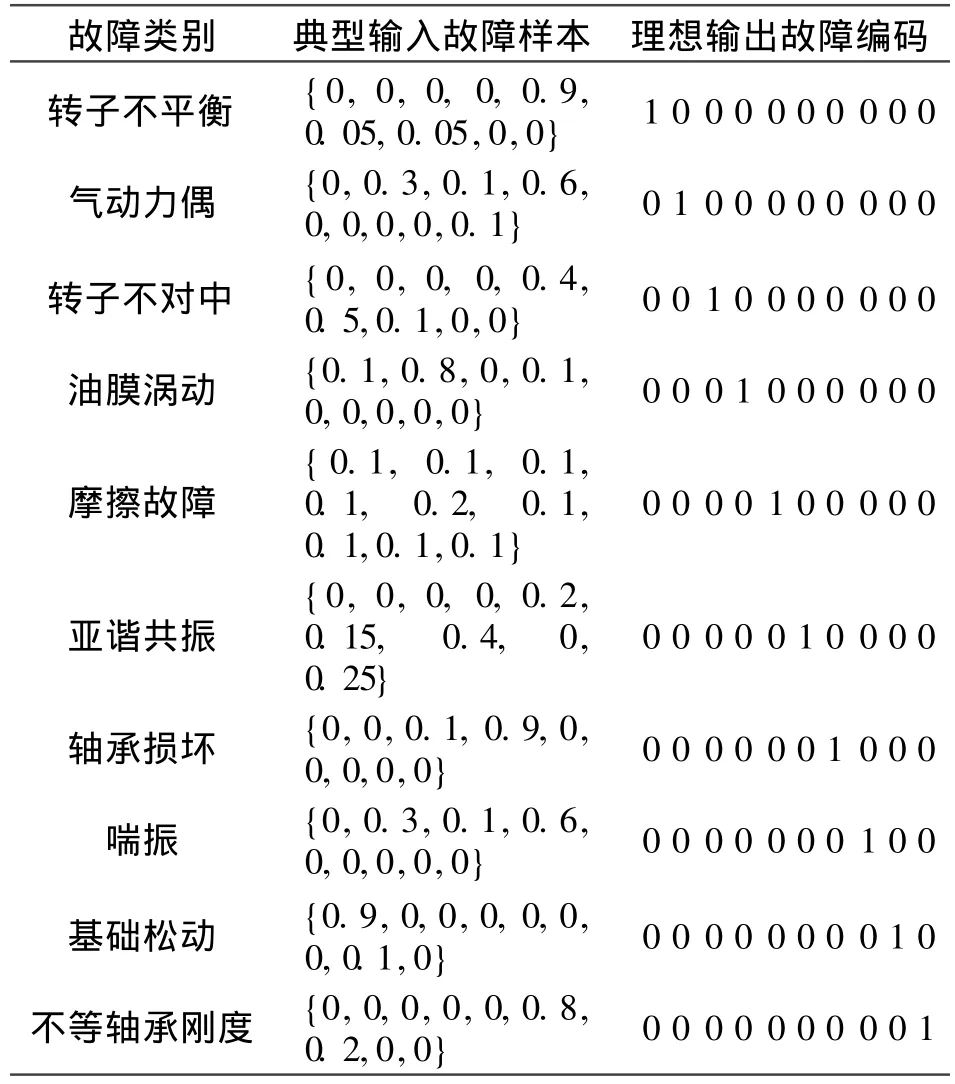
表3 典型故障征兆表

设Xi为加入噪声前的典型故障样本,X′i为加入噪声后的仿真故障样本,仿真样本数据为

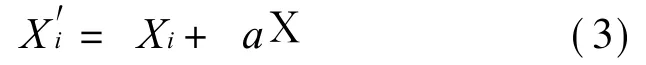
其中:X为人为加入的均值为0、方差为1的随机噪声;a为噪声控制系数,可取a=0.05,0.08,0.12,0.15。

利用式(3)分别对每种典型故障情况产生 60组带噪声的样本,归一化处理后共600组样本。

3.2 仿真研究

基于以上故障样本分析,构建 3层神经网络故障诊断模型,以 ICPSO作为学习算法,称该神经网络为 ICPSO NN。输入层和输出层神经元的个数分别为 9和 10,对应 9维故障模式向量及10位输出故障编码。隐含层的选取根据样本的复杂性及所需达到的泛化能力通过仿真调整,最终节点数定为 12。

从600组样本集中,随机选择180组作为网络训练集(包含 10种故障样本),另选 60组作为测试集。ICPSO的主要参数为:c1=c2=2.0,kmax=0.80,kmin=0.02,最大迭代次数为 3 000,粒子规模为 40,子种群数量为 5,更新周期T=50。训练结束后故障向量及故障编码的映射关系保存在神经网络中。

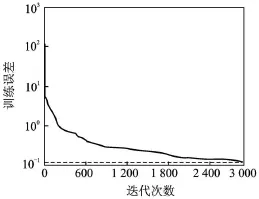
图2 ICPSO NN训练误差曲线

仿真过程引入标准 BP算法和 PSO算法训练相同结构的神经网络(称之为BP NN和PSO NN,其中PSO基本参数与 ICPSO相同),构建同样故障映射,与之形成对比。最大迭代次数都设为3 000,BP网络采用 Matlab6.5中的 TRAINBP函数训练网络。

ICPSO网络的训练误差曲线如图 2所示,BP NN和PSO NN的训练误差曲线如图3所示。ICPSO NN,BP NN和PSO NN的训练误差在3 000次迭代后分别为 0.125,0.421和 0.357。对比结果表明,ICPSO NN表现优于另外两种网络。

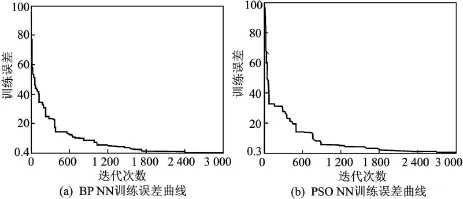
图3 BP NN和 PSO NN训练误差曲线

3.3 试验结果

保存训练好的神经网络的结构、权阈值等数据,人工模拟上述几种故障情况,进行旋转机械在线故障诊断。对故障情况下振动信号进行频谱分析,分离出振动信号的主要频率部分,得出各种振动频率的幅值。预处理后得出相应的故障特征值。将其输入ICPSO神经网络故障诊断系统,网络完成在线计算后得到故障编码(即相应位的值大于 0.5视为“1”,否则为“0”),指示具体故障状态。

表4为部分待诊断数据及诊断输出,结果分别指示为第10,4和6类故障,即不等轴承刚度故障、油膜涡动和亚谐共振故障,与实际相符。采用 ICPSO神经网络可以实现旋转机械的在线故障诊断。

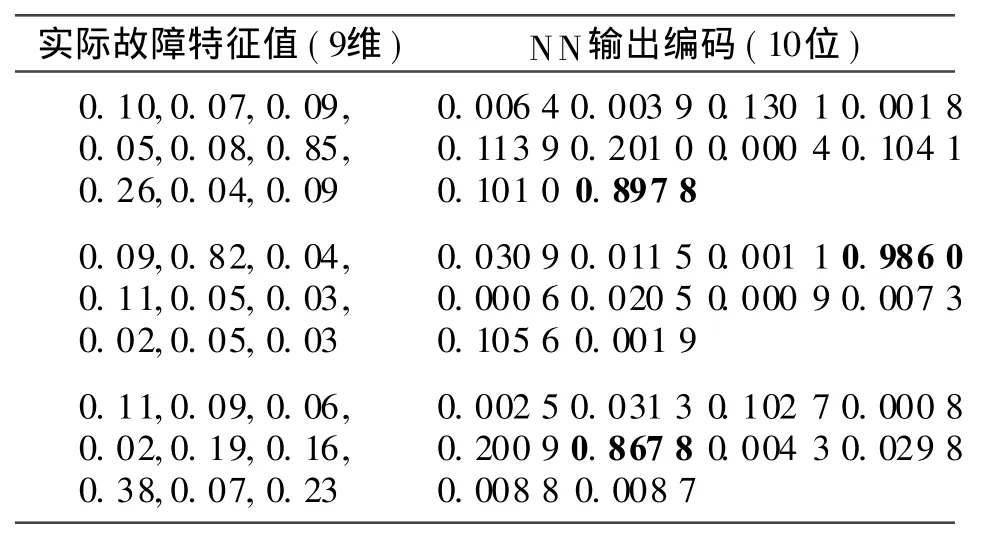
表4 部分试验数据

4 结 论

笔者对 ICPSO方法进行了收敛性分析,以几个经典复杂函数为对象进行了寻优测试并与基本PSO算法进行了比较,分析表明改进算法整体优化性能有显著提高,有效克服了基本 PSO算法在多峰函数寻优时出现的微粒“早熟”现象,为大量非线性、不可微和多峰值复杂优化问题的求解提供了一种新的思路和解决方法。将本方法用于旋转机械神经网络故障诊断建模,设计了相应的在线故障诊断系统。结果表明,该系统具有诊断速度较快、精度较高等特点,适合于旋转机械的在线故障诊断。

[1] 虞和济,陈长征,张省,等.基于神经网络的智能诊断[M].北京:冶金工业出版社,2000:131-136.

[2] 赵冲冲,廖明夫,于潇.基于支持向量机的旋转机械故障诊断 [J].振动、测试与诊断,2006,26(1):53-57.

Zhao Chongchong,Liao Mingfu,Yu Xiao.Application of support vector machine to fault diagnosis of rotation machinery[J].Journal of Vibration,M easurement&Diagnosis,2006,26(1):53-57.(in Chinese)

[3] 唐贵基,向玲,朱永利.基于 HHT的旋转机械油膜涡动和油膜振荡故障特征分析 [J].中国电机工程学报,2008,28(2):77-81.

Tang Guiji,Xiang Ling,Zhu Yongli.Fault analysis of oil whirl and oil whip based on Hilbert-Huang transform for rotor system[J].Proceedings of the CSEE,2008,28(2):77-81.(in Chinese)

[4] 陈如清,沈士根.基于递归神经网络的旋转机械故障诊断方法 [J].振动、测试与诊断,2005,25(3):233-235.

Chen Ruqing,Shen Shigen.Fault diagnosis for rotating machinery based on RNN[J].Journal of Vibration,Measurement& Diagnosis,2005,25(3):233-235.(in Chinese)

[5] 刘静,钟伟才,刘芳,等.组织协同进化分类算法 [J].计算机学报,2003,26(4):446-453.

Liu Jing,Zhong Weicai,Liu Fang,et al.Classification based on organizational coevolutionary algorithm[J].Chinese Journal of Computers,2003,26(4):446-453.(in Chinese)

[6] Frans V D B,Andries P E.A cooperative approach to particle swarm optimization[J].IEEE Transaction on Evolutionary Computation,2004,8(3):225-239.

[7] 王俊年,申群太,沈洪远,等.基于多种群协同进化微粒群算法的径向基神经网络设计 [J].控制理论与应用,2006,23(2):251-255.

Wang Junnian,Shen Quntai,Shen Hongyuan,et al.Evolutionary design of RBF neural network based on multi-species cooperative particleswarm optimizer[J].Control Theory& Applications,2006,23(2):251-255.(in Chinese)

[8] 王元元,曾建潮,谭瑛.多种群协同进化的微粒群算法[J].计算机工程与设计,2007,28(15):3661-3664.

Wang Yuanyuan,Zeng Jianchao,Tan Ying.Cooperative evolutionary particle swarm optimization algorithm with multi-populations[J].Computer Engineering and Design, 2007,28(15):3661-3664. (in Chinese)

[9] Bergh F V D,Engelbrecht A P.A study of particle swarms optimization particle trajectories[J].Information Sciences,2006,176:937-971.

[10]杨妍.智能计算算法的若干研究与应用 [D].上海:华东理工大学,2009.