AGS结构的损伤定位仿真❋

陈振英, 徐志伟, 苟欢敏

(南京航空航天大学智能材料结构航空科技重点实验室 南京,210016)

引 言

格栅结构是美国麦道公司提出的一种新型轻质结构。它具有很多优点,比如三角形格栅结构满足平面点阵结构拉伸主导型几何构形要求,结构承载力高,自稳定性高,抗屈曲能力强,比强度和比刚度高,可以进行多功能设计,便于检测和补修。格栅结构的加强筋相对独立,在冲击荷载作用下,产生的裂纹不易传播,整体性能好[1]。随着先进复合材料的广泛应用及结构先进制造工艺的发展,已成为当代航空、航天、船舶和高速运载机械中最有竞争性的先进结构形式之一。

格栅结构在制造和使用过程中,由于制造工艺的不完善或外来物的冲击等因素,会导致其面板与筋之间出现脱胶,筋板开裂,面板破损。损伤极易导致面板和筋板的局部失稳,乃至整体失稳,最终造成结构的失效。AGS的损伤既有复合材料损伤的一般特质,如复合材料自身的脱层、内部纤维断裂等微观情况下的损伤,又有其特殊性,如组成格栅部分的筋板的宏观结构处的损伤。周期分布的胞元结构的存在,使得损伤的检测变得复杂,因此,实现对这些损伤的检测具有重要的意义。

N.Takeda等对飞机方向舵的格栅结构进行了健康监测研究,提出了针对周期性碳纤维格栅结构的布拉格光栅的埋入和布置的方法,并建立了分布式光纤传感网络对格栅进行监测,应用 FBG传感网络研究了低速冲击下损伤缺陷的监测和定位,并将试验结果和预报模型进行了比较[2-5]。陈浩然等对格栅结构面板的分层损伤进行了研究,采用有限元数值模拟方法,研究了面板内含分层损伤复合材料格栅结构的稳定性问题,以及多种因素对格栅的稳定性特征的影响,实现了分层损伤的扩展动态可视化过程,研究了面板的铺层方式对格栅结构的分层起裂和扩展过程的影响[6-8]。

笔者采用有限元数值模拟方法对等三角形格栅结构进行了模态分析,得到结构损伤前、后的模态振型,针对格栅结构出现的几种典型的宏观损伤,采用模态曲率差法对其进行损伤位置的识别,分析了格栅结构损伤定位分析的可行性和优缺点。

1 模态曲率差方法

针对复合材料结构的损伤检测可分为两大类:局部法和整体法。通常由整体识别法识别出损伤的大致位置,然后由局部法对该处的各部件进行具体的损伤检测。局部法主要有目测法、射线法、超声脉冲法等;整体法大致分为动力指纹分析法、遗传算法、小波分析法和神经网络法等[8]。笔者主要探讨采用整体识别法中的模态曲率方法实现对损伤位置的检测。

利用模态振型来识别损伤有两种途径:一是直接利用结构损伤前、后的振型变化来识别损伤;二是由振型构造结构损伤标识量,由标识量的变化或其取值来识别损伤。

基于曲率反映结构中性面的变形模态与构件的截面弯曲刚度成反比的原理,如果结构发生损伤,损伤处的局部刚度会下降,并导致曲率增大。因此,根据振型曲率的变化可有效地定位损伤[9-11]。

利用中心差分方法可求得结构的模态振型曲率

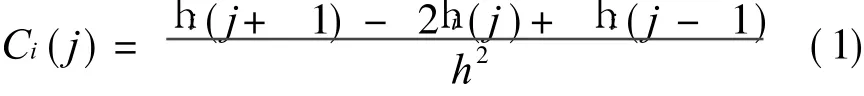
其中:hi(j-1),hi(j)和hi(j-1)分别为第i阶模态在j-1,j,j+1点的模态位移值;h为两节点间的距离。

对于第i阶模态有

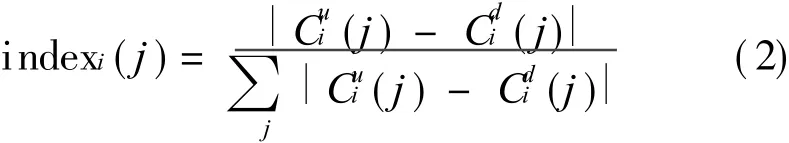
其中:,为损伤前、后的模态曲率。

对于多阶模态,可取index的平均值来检测损伤发生的位置 ,即

MSC最大的地方就是最有可能发生损伤的位置,通过 MSC的变化可确定结构的损伤位置。

2 格栅结构典型损伤定位的仿真

选取图 1所示的等三角形格栅结构为研究对象,结构的一侧附有面板[12]。尺寸为:L×B×H=104 mm×320 mm×15 mm,胞元的边长a=80 mm,筋板和面板厚度均为t=1 mm。材料参数为:弹性模量E= 15.9 GPa,泊松 比 _=0.3,密度 d=1 750 kg/m3,尺寸如图 2所示。

选取如图 3所示格栅结构筋板的交叉点以及筋的中点作为计算节点,这些节点均位于格栅结构的面板上。图3中标记了所分析筋板的编号,共31个筋板,49个节点。对于每条筋板,通过选取两端和中点处的模态位移值,计算在中点位置处的模态曲率,以 31个筋板中点位置处的模态曲率差作为损伤标识指标。

仿真分析时,图 1中结构左端固支,右端简支,进行模态分析。

图1 格栅加筋结构示意图

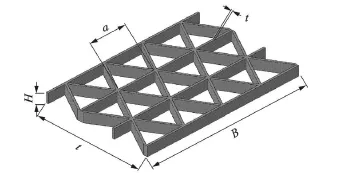
图2 格栅结构尺寸示意图

图3 关键点及筋板编号的示意图

2.1 单损伤状况分析

笔者针对复合材料结构常见的 3种损伤形式:面板与筋板的脱层、筋板开裂和面板的破损,对它们单独在某一个位置处发生时的情况进行分析。

2.1.1 面板与筋板的脱层损伤

有限元结构建模中,在筋与面板的连接处,去掉1 mm宽度的筋板以模拟该损伤形式,如图 4所示,所计算的损伤在筋板L13处。损伤前、后格栅结构模态频率的变化如表 1所示。

图4 脱层损伤示意图

表1 L13处发生脱层损伤时的频率变化 Hz

出现局部较小的损伤时,结构频率的变化不会很大,但表 1中的某些频率发生了较大的变化,通过振型分析发现:损伤后第3阶、第5阶模态频率对应的是局部模态,与损伤前的模态不对应,因此不能用于对比计算。将损伤前的 1,2,3,4阶模态与损伤后的1,2,4,6阶模态振型相对应,各对应阶次的频率变化均不超过 1%,用这些数据做计算分析,结果如图5所示。

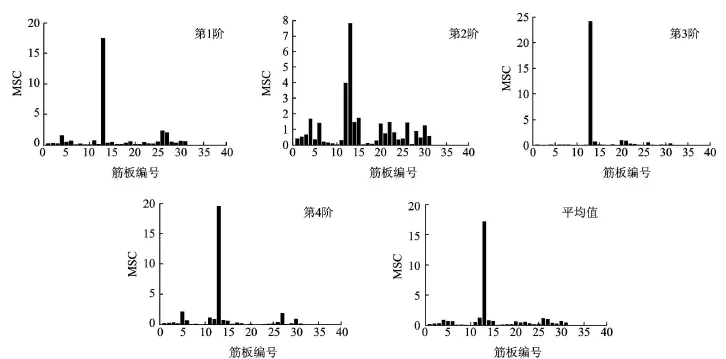
图5 L13单脱层损伤时 M SC的计算结果

由以上结果可以看出,所有 4阶模态MSC最大值均在 L13所对应的位置处。第1,3,4阶模态MSC最大值均大于 15,其余无损伤处的值均小于2。第2阶模态 MSC最大值为 7.8,在与其相邻的 L12处的值是4.1,其余无损伤处的值均小于 2。

在 L13处,前 4阶模态 MSC平均值的最大值为17.1,而其余无损伤处的值均小于2,远远小于17.1,损伤的位置可确定下来。

2.1.2 筋板开裂损伤

当筋板出现损伤时,对结构的性能有较大的影响。笔者采用2 mm宽的缺口(在L10筋板的中间位置处)来模拟这种损伤,如图6所示。结构模态频率的计算结果如表 2所示。

图6 开裂损伤示意图

从损伤前、后频率的变化来看,各对应阶次的频率变化均小于3%。对比振型后发现,没有局部模态产生,因此将前4阶模态值作为计算数据,计算结果如图 7所示。第1,2阶模态的M SC最大值在 L10处,均大于10,其余筋板处的MSC值均小于3。第3,4阶模态的 MSC最大值也在 L10处,分别是 8和 5.5。前4阶模态 MSC平均值的最大值为 9.6,在 L10处,远大于其他筋板处所对应的 MSC平均值,因此可以确定损伤的位置。

表2 L10处发生开裂时的频率变化 Hz

2.1.3 面板损伤

面板上的损伤通过一圆孔来模拟,半径为10 mm,如图 8所示,损伤在 L18,L19和 L29这 3个筋板所围成的三角区域内。结构模态频率的计算结果如表3所示。

表3 面板损伤时结构频率的变化 Hz

和表 2的状况类似,没有局部模态产生,且各对应阶次的频率变化均不超过 1 Hz,面板出现损伤对于结构的性能影响较小。取其前 4阶模态值进行计算,计算结果如图 9所示。在 1阶模态的结果中,MSC值最大的3个值于L18,L19,L29处分别为5.7,3.2,7.3,由这 3组数据可确定损伤所在的区域。但是第2阶到第4阶以及平均值的计算结果却不能辨识出损伤所在区域,而且前4阶MSC的平均值也很小,除 L21处为 3.6,其余均小于 3。

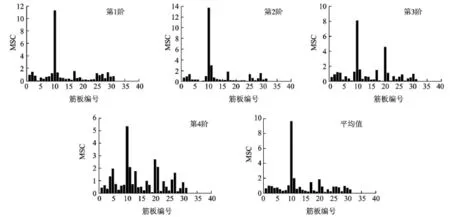
图7 L10筋板开裂损伤时M SC的计算结果

图8 面板损伤示意图

2.2 多损伤状况

从前面结果可以看出,在单个损伤发生时,采用1阶模态值进行模态曲率差的计算,可得到比较好的辨识结果。当出现多损伤时,采用1阶模态的计算不能得到满意的结果,下面通过算例来分析多损伤发生时的计算情况。

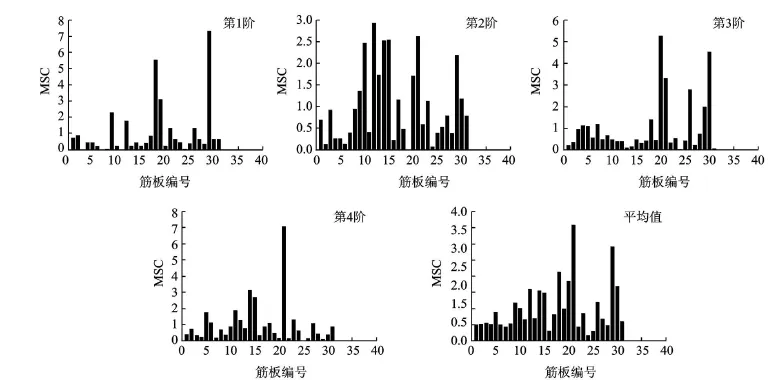
图9 L18-L19-L29面板损伤时 MSC的计算结果

笔者共计算了 4种多损伤状况:两处脱胶、两处筋开裂、一处脱胶一处开裂、破损脱胶开裂同时存在。损伤程度与前面所述的3种单独损伤的程度一致。下面给出第1阶模态计算和前3阶模态平均计算的结果比较,在计算中已经排除了局部振动时的数据。

由图 10可看出,脱层损伤的两处位置 L13和L24的 MSC的值分别为 20.1和 6.2,远大于其他位置处的值,两处损伤的位置可以确定。其余3种损伤状况只能识别出位于纵向筋板(L25～ L31)位置上的1个损伤。

图10 多损伤时 1阶模态下 MSC的计算结果

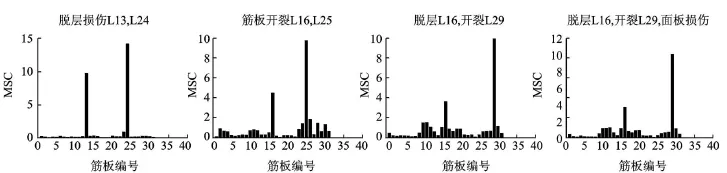
图11 多损伤时前 3阶模态 MSC的平均计算结果

前3阶模态平均值结果如图11所示。图11中,脱层损伤 L13和 L24处的 MSC值分别为 9.9和14.5;开裂损伤 L16和 L25的 MSC值分别为 4.7和9.8;脱层开裂同时存在时,L16和 L29的 MSC值分别为3.7和10.0;最后 3种损伤同时存在的状况下,L16和 L29的 MSC值分别为 3.9和 10.1。若采用 3阶模态平均计算的结果,4种损伤情况都能得到正确辨识。

当前的约束条件下,在结构的纵向筋板(L25～L31)处发生损伤时,作为结构的承弯部分,其模态曲率的变化也是最大的。在 1阶模态(弯曲)的计算结果中,斜向筋板上的损伤会被掩盖掉,这在3阶平均(考虑了扭转)的计算结果中有了一定的改善。从数值上看,斜向筋板上的MSC的值虽然仍小于纵向筋板上的值,却远大于无损伤处的 MSC值,因此可以确定损伤的位置。

3 结 论

1)采用曲率差方法能够对结构筋板上的损伤进行识别,在前3阶模态的平均值结果下,通过MSC值的分析可确定筋板上损伤的位置所在。

2)在前 3阶模态中,当出现损伤时,损伤处的MSC值一般远大于无损伤处的,通常MSC值大于 3时,就有发生损伤的可能,因此需要对可能出现的误判加以注意。

3)对于面板上的损伤,其定位效果较差,在多损伤状态下无法做出有效判断。但是,面板的损伤对结构的刚度影响不大,因此,对于结构本身不会有太大的影响。

[1] Takeya H,Ozaki T,Takeda N.Structural health monitoring of advanced grid structure using multipoint FBG sensors[J].Proceedings of SPIE,2005(5762):204-211.

[2] 杜善义,章继峰,张博明.先进复合材料格栅结构(AGS)应用与研究进展 [J].航空学报,2007,28(2):419-424.

Du Shanyi,Zhang Jifeng,Zhang Boming.Overview of application and research on advanced composite grid structures[J].Acta Aeronautica et Astronautica Sinica,2007,28(2):419-424.(in Chinese)

[3] Amano M,Takahashi I,Okabe Y,et al.Identification of damage location in advanced grid structures usingfiber Bragg grating sensor[J].Proceedings of SPIE,2005(5765):644-655.

[4] Amano M,Okabe Y,Takeda N,et al.Structural health monitoring of advanced grid structure with embedded-fiber Bragg grating sensors[J]. Structural Health Monitoring in Press,2007,6(4)::309-324.

[5] Amano M,Arai T,Takeda N.Guided wave diagnosis in composite grid structure with embedded FBG sensors[J].Proceedings of SPIE,2007(6530):65300.

[6] 白瑞祥,王蔓,陈浩然.含损伤复合材料 AGS板的屈曲特性[J].复合材料学报,2008,22(4):136-141.

Bai Ruixiang,Wang Man,Chen Haoran.Buckling behavior of composite AGS with delamination[J].Acta Materiae Compositae Sinica,2008,22(4):136-141.(in Chinese)

[7] 于瑾,陈浩然,白瑞祥.含分层损伤 AGS起裂和扩展过程数值模拟 [J].大连理工大学学报,2008,48(4):469-474.

Yu Jin,Chen Haoran,Bai Ruixiang.Numberical simulation of delamination onset and growth process for advanced composite grid stiffened structures[J].Journal of Dalian University of Technology,2008,48(4):469-474.(in Chinese)

[8] 陈浩然,于瑾,白瑞祥.含分层损伤复合材料等三角形格栅加筋板的起裂和扩展过程研究 [J].复合材料学报,2008,25(2):173-177.

Chen Haoran,Yu Jin,Bai Ruixiang.Study on delamination onset and growth process for composite advanced isogrid stiffened structures(AGS)[J]. Acta Materiae Compositae Sinica,2008,25(2):173-177.(in Chinese)

[9]易登军,韩晓林.损伤结构的实验曲率模态研究 [J].振动、测试与诊断,2004,24(3):234-237.

YiDengjun, Han Xiaolin. Experimental curature modal analysis of damaged structures[J].Journal of Vibration,Measurement& Diagnosis,2004,24(3):234-237.(in Chinese)

[10]罗晓健,于国有.几种模态分析方法在结构无损检测中的应用 [J].中国海洋平台,2006,21(5):44-49.

Luo Xiaojian,Yu Guoyou.Application of modal analysis methods in non-destructive damage evaluations[J].China Offshore Platform,2006,21(5):44-49.(in Chinese)

[11]姜峰.模态曲率差技术在薄板损伤检测中的应用 [D].西安:西安理工大学,2008.

[12]苟欢敏,徐志伟,李飞,等.复合材料格栅结构的力学性能研究[J].兵器材料科学与工程,2009,32(6):19-22.

Gou Huanmin,Xu Zhiwei,Li Fei,et al.Research on mechanical properties of composite grid structures[J].Ordnance Material Science and Engineering,2009,32(6):19-22.(in Chinese)