异常载荷剔除中幅值与梯度门限的联合应用❋
王宏健, 王继新, 王乃祥
引 言
工程机械传动系测试载荷数据处理中,异常数据的剔除是较为棘手的问题。对原始信号奇异值的处理可以转化为求解轨道矩阵的最佳逼近问题,降噪效果由逼近情况而定[1]。除了小波理论应用在载荷谱信号中奇异信号的剔除与降噪外[2-3],现有的解决途径一般是基于正态分布、指数分布或Weibull分布假设,以残差为分析对象[4-5],以样本数据标准差为尺度进行异常数据的判别与剔除,样本量不同时对数据或其残差所假设的分布也不相同[4]。这样就会遇到两个问题:a.实际数据是否真的为假设分布类型;b.即便分布类型准确,以样本数据为基础确定的标准差,极有可能己经受到异常数据的很大影响,那么以此标准差作为剔除数据尺度,必然会产生非期望误差,大大降低异常数据剔除的有效性。文献[6]指出了最小二乘法中用残差大小来判断异常值是不可靠的。为了解决上述问题,可以将异常数据排除在统计分析样本数据之外,或者在估计统计分析结果时排除异常数据的影响。文献[7]引入锐化因子,通过对梯度门限和锐化参数强度适当选取,改进了传统滤波器。文献[8-10]对Perona-Malik模型进行了改进,基于图像空间坐标,使用同一个梯度门限进行扩散除噪。文献[11]提出了一种基于平稳小波域去噪方法,在低频子带和高频子带上分别采用不同的梯度门限进行各向异性扩散滤波后的重建。
由于数据的承载体是机械构件,笔者以装载机为例,除了对数据进行分析外,还从异常数据的产生机理、实际载荷分布形态以及物理量限值等多角度对异常数据进行了分析和识别。通过对其传动系载荷特点的分析,指出了综合运用幅值门限法与梯度门限法剔除异常数据的优势。
1 传动系载荷特性分析
工程机械的作业环境与作业方式决定了其构件的受载特性。以轮式装载机的“V型六段”的作业方式为例,可以看出在不同作业段的载荷差异十分明显,分段作业的特性非常显著,如图1所示。因此,对于装载机传动系载荷来说,进行载荷数据分析时不仅要在不同工况框架内进行,而且对于单一工况下的一个作业循环内的载荷数据也要区分开来,并将相同作业段的载荷数据编排到一起,这样才使数据具有合理稳定的统计分布规律,异常数据的有效剔除才成为可能。
在样本量n>50的条件下,其统计推断的结果较接近于总体统计特性。本次以小石方工况为例,测得了 74次循环作业下的传动系中间法兰载荷,铲掘作业段载荷编排连接后的局部如图 2所示。
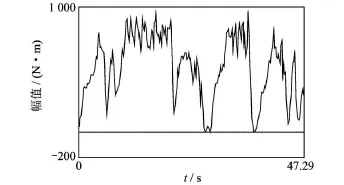
图1 装载机循环作业时的典型扭矩时间历程
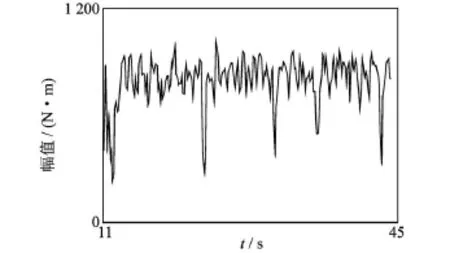
图2 中间法兰铲掘作业段连接后局部扭矩时间历程
2 异常载荷数据剔除方法
2.1 载荷信号的测取
采用近程遥测技术获取本次试验的载荷数据。正式测试前先进行扭矩测试系统标定工作,将扭矩信号与测得的电压信号建立起连接。测试时,采用遥测仪将应变片式扭矩传感器获取的扭矩信号发射出来,信号采集系统同步记录,采样频率为100 Hz,载荷信号的测取方式如图 3所示。

图3 载荷信号测取框图
2.2 异常数据常规剔除方法
异常数据又称奇异点或野点。仔细观察采集到的信号时间历程,可以看出夹杂着大量的奇异点。这些奇异点的产生原因是多方面的,例如测试元件的电压变化、电磁干扰或者测试系统受到异常振动等。这些非实际载荷的异常数据必须剔除或将其影响排除掉,否则对实际载荷大小估计及以后的构件疲劳寿命估计都有很大影响。当前剔除异常数据已有多种方法:3e准则、格拉布斯(Grubbs)准则、肖维勒(Chauvenet)准则、狄克逊 (Dixon)准则和t检验法等。
3e准则表达式为
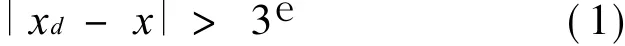
其中:xd为样本数据;x为样本均值。
当某个样本数据符合上式时,则认为它是异常的,应予剔除。
格拉布斯准则表达式为

其中:s为该系列数据的标准偏差;G(a,n)为格拉布斯检验临界值;a为检出水平;n为测量次数。
另外几种检验异常数据的原理基本相似,都是假设样本数据服从某种分布(多数认为是正态分布)的前提下,通过概率统计分析等途径求得标准差等界限标定,进而进行异常数据的剔除。实际上,测试所得到的随机信号并不一定真实服从正态或其他分布,因而剔除效果并不理想。有些方法过于敏感,在剔除奇异点的同时也去掉了一些有用的数据。
3 幅值门限法与梯度门限法的联合应用
3.1 门限检测方法基本原理
幅值门限检测法适用于幅值相对正常载荷大的奇异点。门限值主要通过观察幅值概率分布图来选取,一般情况下,奇异点位于主要分布区域以外。
梯度门限检测法主要通过对原始信号的差分求导,得到信号的梯度,再由梯度的概率分布确定门限值的选取。通常它所识别的奇异点的梯度要高于正常信号的梯度。根据这一特点,可设定一个梯度门限值,将小概率、梯度较大的信号剔除。
3.2 异常数据剔除方法的比较
将中间法兰扭矩载荷信号分别进行幅值门限检测、梯度门限检测以及传统的基于概率密度分布的标准差检测,检测分析的结果分别如图4、图5和图6所示。

图4 奇异载荷的幅值门限检测结果
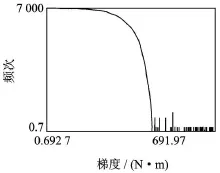
图5 奇异载荷的梯度门限检测结果
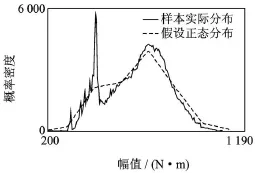
图6 奇异载荷基于概率密度分布的标准差检测结果
由幅值门限法、梯度门限法以及基于概率密度分布的标准差检测的基本原理可以看出,因判别异常数据的原理不同,其适用范围也不同。进行载荷信号异常数据处理时,要具体问题具体分析,选择与信号特点相适应的方法进行处理,才能收到较好的效果。如图6所示,如果按假设估计值进行统计,其所得数据的均值、方差等参数,将明显与实际载荷数据分布特征不符。同时,nSoft软件检测的奇异点列表也表明,即使在选择 9倍方差进行门限值滤波的情况下,检测出的奇异点仍明显偏多,这说明标准方差法不大适用于这种测试信号的处理。
3.3 门限值的选定
应用门限检测对载荷数据奇异点进行处理时,关键在于门限值的选取。不同的门限值得到的处理结果有所差异。如图 4所示,幅值门限检测时,幅值分布可分为两部分,即连续部分与断续部分,断续部分又分为低幅断续和高幅断续。因此这里选定双门限将奇异点剔除,设定高门限和低门限分别为v1和v2,其中v1<v2。处于低幅断续的数据由于其数量相对数据总量小几个数量级,且其值很小,对传动系寿命影响甚微,故令v1等于最小连续分布幅值。而v2的选取,考虑到实际工况的复杂性,即使高断续幅值的出现频次很低,也不能简单以幅值分布的连续、断续分界点为门限阀值。这里令v2=min[p×Gcontinue],其中:p为门限值系数;Gcontinue为最大连续分布幅值,大小依工况而定。
梯度门限检测时,一般考虑用最大梯度的百分比自动决定门限,即TG=pGmax,其中:p为百分比;Gmax为整个载荷梯度的最大值[12]。这一梯度门限的选法是有缺陷的:实际载荷数据会出现个别梯度极其异常的极端情况,导致百分比的选择波动较大,检测结果的稳定性较差。为此改用以最大连续梯度为基准作为更稳定的梯度门限,即TG=pGcontinue,p>1。传动系载荷样本数据量一般在50 000以上(本试验数据量为 82 796),个别数据以极大梯度逃出此量级的连续梯度分布离散形式出现,依数理统计理论可知,此种情况出现概率甚微。由大量试验统计数据证明,p值选在 1~1.1之间最为合适,既实现了梯度基准剔除异常数据的期望准确度,又与实际工况载荷状况相吻合。
3.4 异常数据的有效剔除
3.4.1 幅值门限法检测异常数据
检测结果如图 7所示,其中所标识出的异常数据即为图 4中幅值大于 1 133 N◦ m不连续扭矩的幅值,共计10个点。按其中最大幅值的1 193 N◦ m计算,也仅仅超出连续幅值 5%,并且从装载机实际工作状况来看,这些数值完全可以在样本数据中产生,故这里不认为是异常数据,不予剔除。

图7 幅值门限检测法测得的扭矩载荷异常数据
3.4.2 梯度门限法检测异常数据
检测结果如表 1所示,在时间历程中的位置如图8所示。经时间历程局部放大后发现,这些点的分布似乎符合某种规律。在图中获取精确坐标即可知,均为不同作业循环连接的交界处。因为无论信号的采集多精确,客观的实际载荷均不能保正前一铲掘作业段末点与后一铲掘作业段始点相一致,故此处幅值的梯度超限机率非常大。本例中梯度超限点占总连接数的81%,可见剔除工作是必要的。
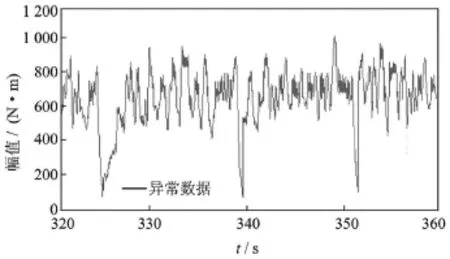
图8 梯度门限检测法测得的扭矩载荷异常数据
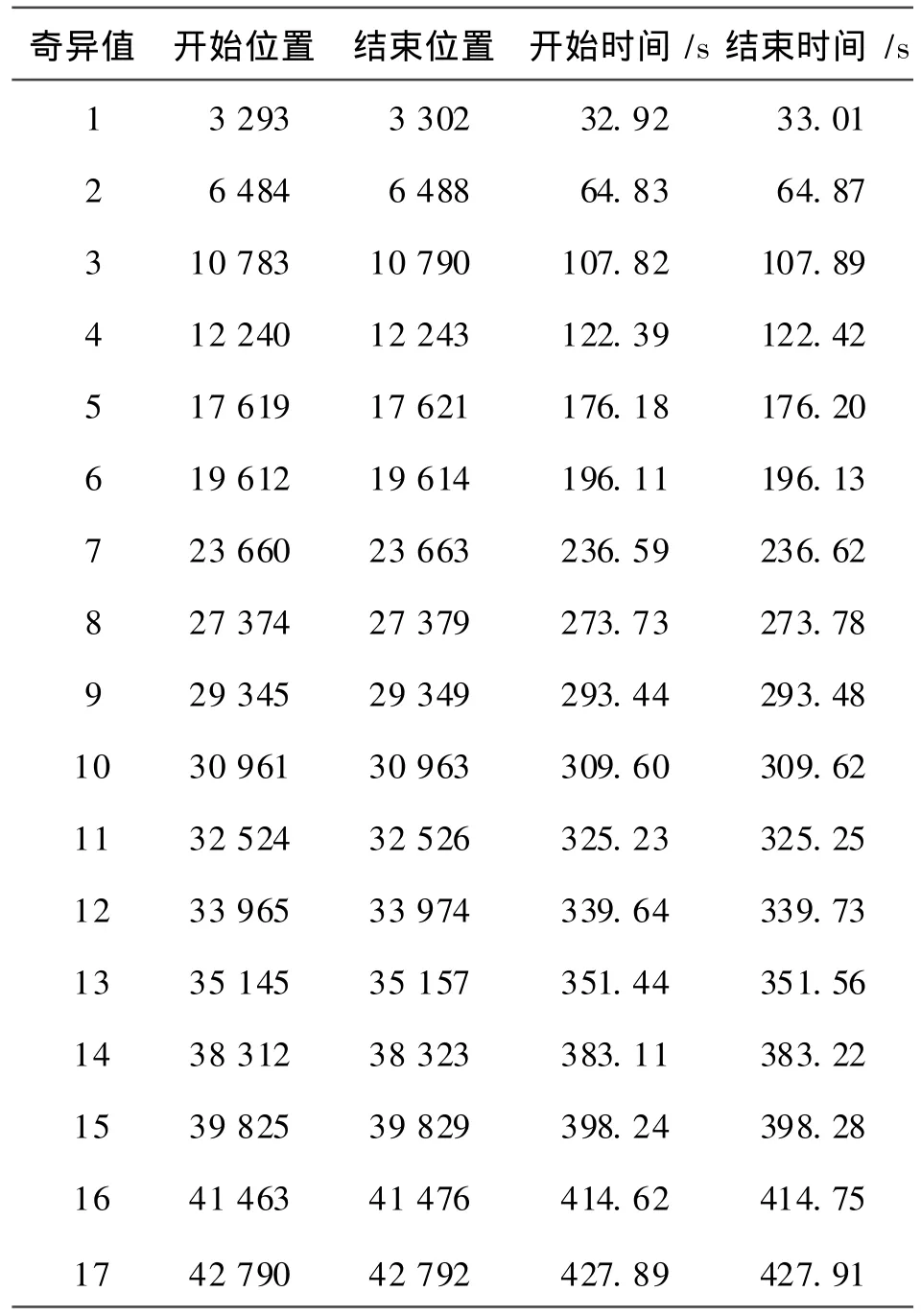
表1 梯度门限法剔除的异常数据(采样频率为100 Hz)
3.4.3 幅值门限法与梯度门限法的综合运用
综合运用幅值门限法与梯度门限法剔除异常数据后的时间历程如图 9所示。幅值门限法对于大误差的和超数量级的异常数据具有良好的识别性,梯度门限法对于小幅值的奇异点检测能力强,这两种方法结合去除奇异值的满意度是传统的概率统计方法很难达到的。
4 结束语

图9 幅值门限与梯度门限综合运用下载荷异常数据的剔除
针对传统方法基于假定样本数据服从某种典型概率分布,利用标准差剔除异常数据的方法存在的固有局限性,提出了幅值门限和梯度门限综合运用去除奇异值的方法。由试验数据处理结果可知,此方法不仅可以去除大幅值奇异值,还可以对小幅值的奇异值成功去除。对于隐含在正常数据中的小偏差异常数据,同样具有良好的检测性。同时,幅值门限和梯度门限的联合应用不以数据服从哪种具体的概率分布假设为前题,避免了人为主观判断和对概率分布函数进行参数估计,也就避免了由于样本含有异常数据而导致求得的分布参数的不准确性。
[1] 孙鑫晖,张令弥,王彤.基于奇异值分解的频响函数降噪方法 [J].振动、测试与诊断,2009,29(3):325-328.
Sun Xinhui,Zhang Lingmi,Wang Tong.Noise reduction of frequency response function using singular value decomposition[J].Journal of Vibration,Measurement& Diagnosis,2009,29(3):325-328.(in Chinese)
[2] 王国军,蒋美华,王俊.载荷谱信号奇异值剔除与降噪处理 [J].仪器仪表学报,2009,30(6):311-313.
WangGuojun,JiangMeihua,WangJun.Remove spike and noise in the load spectrum method[J].Chinese Journal of Science Instrument,2009,30(6):311-313.(in Chinese)
[3] 向东阳,吴正国,胡文彪,等.改进的小波变换系数相关去噪方法 [J].振动、测试与诊断,2010,10(5):561-565.Xiang Dongyang,Wu Zhengguo,Hu Wenbiao,et al.Improved denoising algorithm using correlation of wavelet coefficient[J].Journal of Vibration,Measurement& Diagnosis,2010,10(5):561-565.(in Chinese)
[4] 林洪桦.剔除异常数据的稳健性处理方法[J].中国计量学院学报,2004,15(1):20-24.
Lin Honghua.The robustness data processing method about eliminating outlier[J].Journal of China Jiliang University,2004,15(1):20-24.(in Chinese)
[5] Wilcox R R.Introduction to robust estimation and hypo thesis testing[M].San Diego: Academic Press,1997:34-36.
[6] 孙士兵,赵欢.一种异常数据诊断应用的稳健回归算法[J].科学技术与工程,2007,7(15):3728-3730.
Sun Shibing,Zhao Huan.Steady return algorithm in the abnormity data diagnoses and application[J].Science Technology and Engineering,2007,7(15):3728-3730.(in Chinese)
[7] 汪伟,吴秀清,程蕾,等.基于平稳小波域的各向异性扩散图像去噪方法 [J].计算机工程与应用,2010,46(4):180-182.
Wang Wei,Wu Xiuqing,Ceng Lei,et al.Image denoising based on stationary wavelet-based anisotropic diffusion[J].ComputerEngineering and Applications,2010,46(4):180-182.(in Chinese)
[8] Black M J,Sapiro G,Marimont D H,et al.Robust anisotropic diffusion[C]∥IEEE Transactions on Image Processing.Palo Alto:IEEE,1998:421-432.
[9] Voci F,Eiho S,Sugimoto N,et al.Estimating the gradient in the Perona-Malik equation[C]∥IEEE Signal Processing Magazine.Kyoto:IEEE,2004:39-46,65.
[10]Catte F,Lions P L,Morel JM,et al.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal on Numerical Analysis,1992,29(1):182-193.
[11]程哲,胡茑庆 ,冯占辉,等.基于动力学仿真的行星轮系损伤检测方法 [J].振动、测试与诊断,2010,30(4):379-383.
Cheng Zhe,Hu Niaoqing,Feng Zhanhui,et al.Detection of damage in planetary gear sets based on dynamical simulation[J]. Journal of Vibration,Measurement& Diagnosis,2010,30(4):379-383.(in Chinese)
[12]闰成新,范波涛.基于梯度门限的图像过渡区提取与分割 [C]∥第一届中国图学大会论文集.烟台:中国学术期刊电子出版社,2007:318-320.

