一般非线性离散系统P－D 型迭代学习收敛性研究

刘长良，贾万根

0 引言

迭代学习控制 (Iterative Learning Control，ILC)作为学习控制的一个重要研究方向，是智能系统中具有严格数学描述的一个分支。自Arimoto开创性的提出迭代学习控制概念以来，研究人员针对不同类型的对象［1～6］，提出了形式多样的迭代学习控制律［7～11］，并在一定的前提假设条件下，利用微积分不等式、Lyapunov 理论、λ 范数、2 －D 理论等各种数学工具，分析得到了收敛性的条件。虽然迭代学习控制一直是控制界的研究热点领域之一，但大多只是针对一类特定的系统。对于一般的非线性系统，由于结构、参数等很不确定而且非线性环节的存在使得系统控制器的研究变得复杂，所以针对一般的非线性系统的研究成果相对较少。文献［12］给出了一般非线性离散系统开环PID 的迭代学习控制收敛性的充分条件及实现条件，并做了严格的数学证明。然而，理论研究表明［13］:闭环迭代律的控制性能比开环控制性能要好，收敛速度也较快。因此，文献［14］在文献［12］的基础上应用范数和归纳法理论，证明了一般非线性离散系统闭环P 型迭代学习控制的收敛性。为了同时利用系统当前运行和前次运行的信息，以便进一步改善控制性能，本文针对一般的非线性离散系统给出了P-D 型开闭环迭代学习控制收敛性的充分条件。

1 问题描述

考虑一般的非线性离散系统

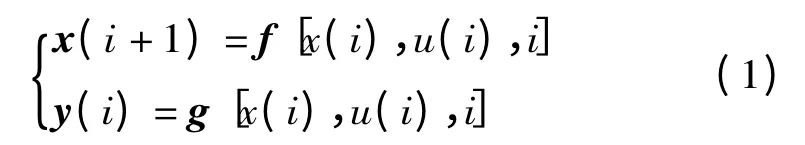
其中，

x(i)∈Rn×1;u(i)∈Rm×1;y∈Rr×1;f，g 为矩阵函数。系统结构和参数未知。所要解决的问题是:要求系统在给定的时间区间［0，N ］上跟踪期望输出yd(i)。假设期望控制ud(i)存在，即:在给定状态初值x (0)下ud(i)是上述方程组的解，则迭代控制的目的是通过多次重复的运动，在一定的学习律下使

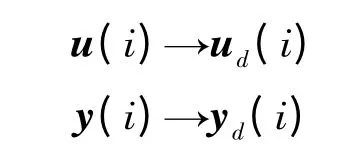
第k 次运行时离散系统表达式为

输出误差为

2 非线性离散的P-D 型开闭环迭代学习收敛性

取开闭环P-D 型控制律，即其开环采用D 型ILC，闭环采用P 型ILC。

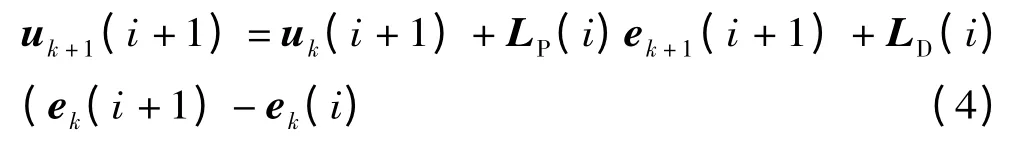
式中:k 为迭代次数;LP(i)为闭环迭代系数;LD(i)为开环迭代系数。

定义1 定义误差函数的λ 范数为

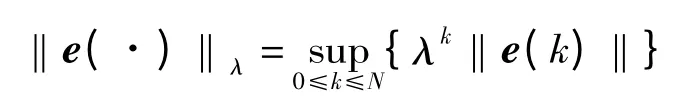
其中，0 ＜λ ＜1。

定理1 如果系统(1)满足条件:

(1)f，g 是连续的函数矩阵。

(2)f，g 关于x，u 的偏导数存在，且满足Lipschitz 条件。记f，g 在第k 次迭代时关于x，u的偏导数分别为fxk，fuk，gxk，guk。

(3)每次学习时的初始状态、初始控制量都相同xk(0)=x0，uk(0)=u0。

(4)矩阵(I + gukLP(i))－1存在 (I 为单位阵)。则非线性离散系统 (1)采用学习律 (4)进行迭代学习控制，输出y (i)以任意精度跟踪期望输出yd(i)的充分条件为

证明:取第k+1 次迭代时的误差函数

将开闭环P-D 型迭代学习控制律(4)代入上式得

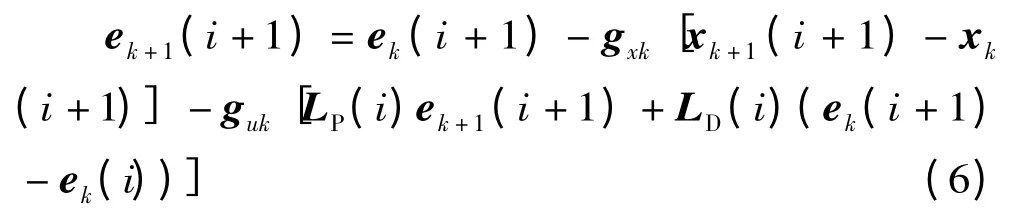
即

由条件(4)

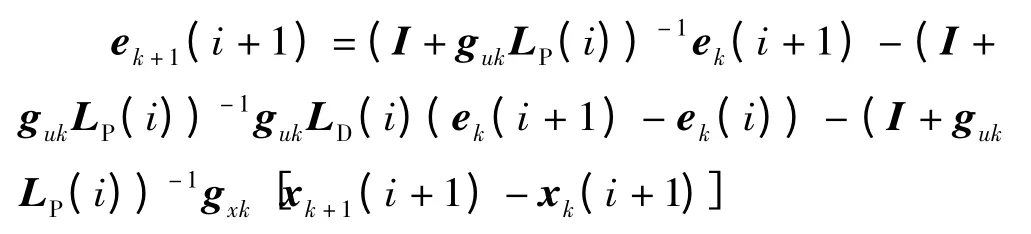
两边同乘λi+1，(0 ＜λ ＜1)

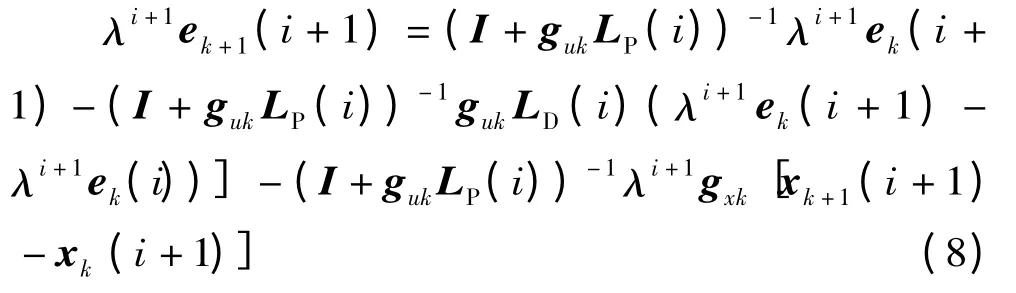
两边同取范数，有

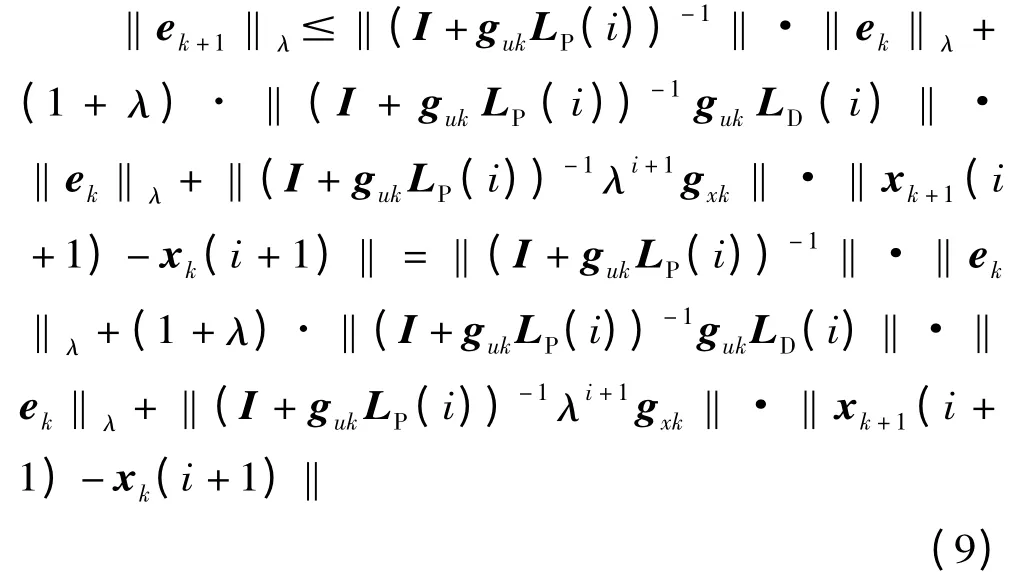
下面用数学归纳法证明:

当i+1 =0 时，据定理1 中条件(3)得

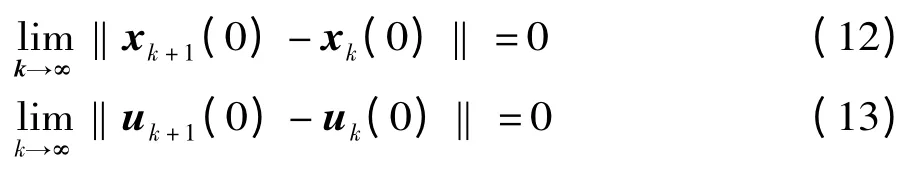
假设当i+1 =n 时，有

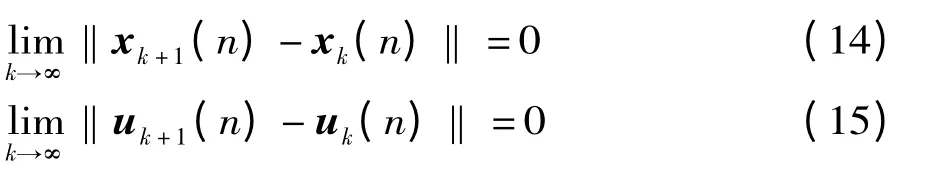
成立，则

当i+1 =n+1 时，

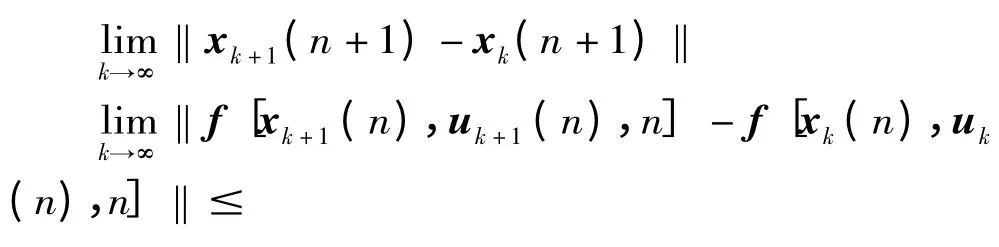
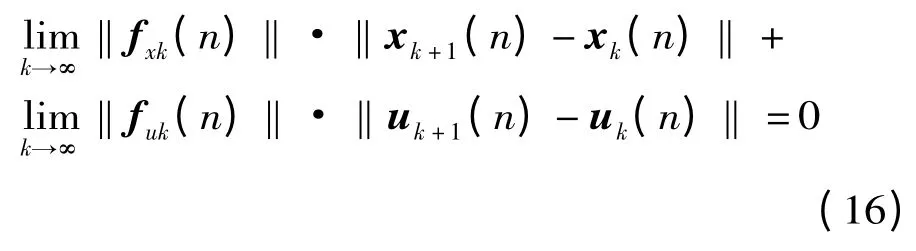
因为0 ＜λ ＜1，故

由定理1 的充分条件式(9)、式(16)及上式，有

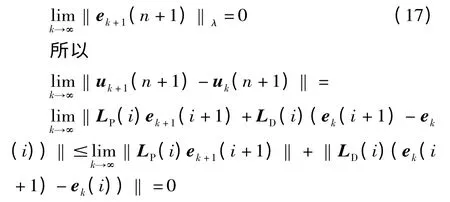
所以，式(10)，(11)成立，定理得证。

3 仿真实例

根据针对一般非线性离散系统的开闭环P-D型迭代学习控制算法的收敛性证明，为了表明该算法的有效性，特此考虑如下非线性离散系统:

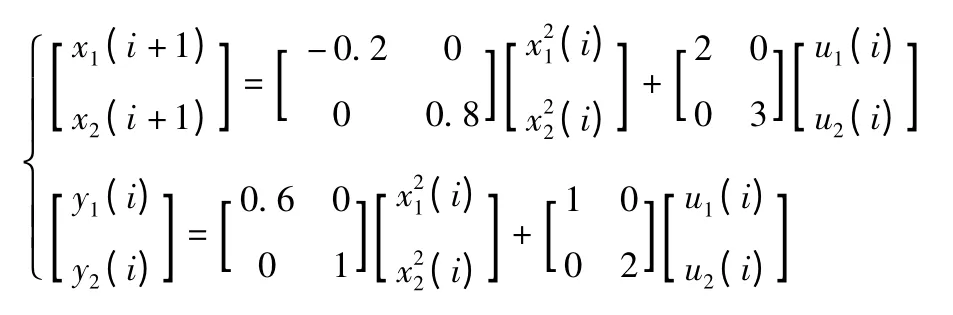
应用上述开闭环P-D 型控制律

设期望输出

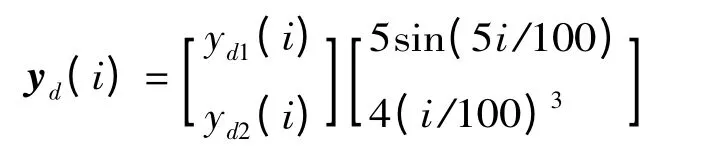
控制律(4)中LP(i)，LD(i)分别取

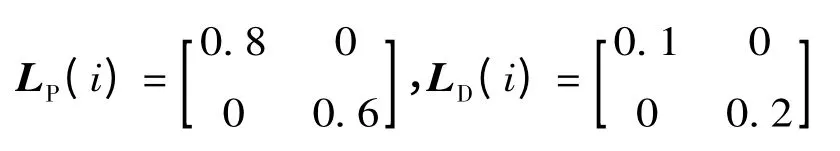
满足条件

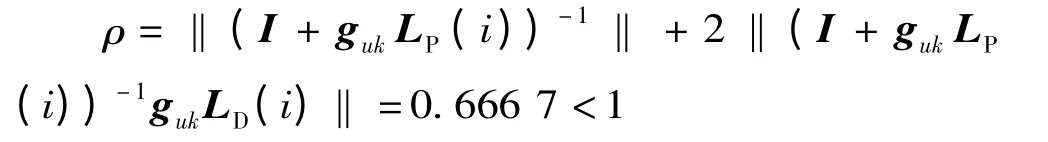
在初始状态为零的条件下，算法(4)跟踪期望轨迹的仿真结果如图1 和图2 所示。图1 是算法(4)在第3 和第5 次时关于期望轨迹第一分量的跟踪情况，而图2 是算法(4)在第3 和第5次时关于期望轨迹第二分量的跟踪情况。从图1和图2 可以看出，当第5 次迭代时算法(4)几乎已经能实现完全跟踪。从图3 和图4 可以很清楚地看出误差最大值随迭代次数的变化情况。

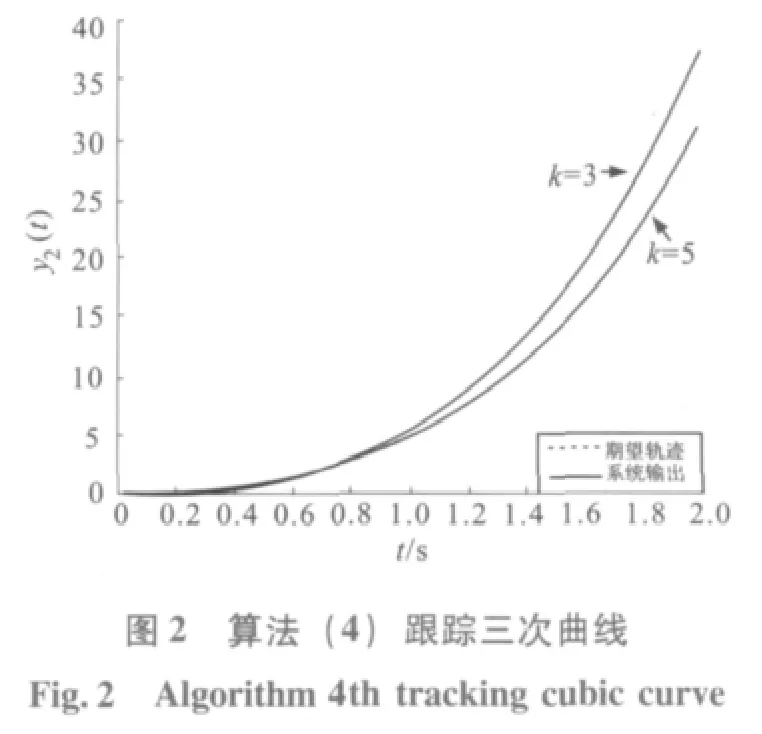
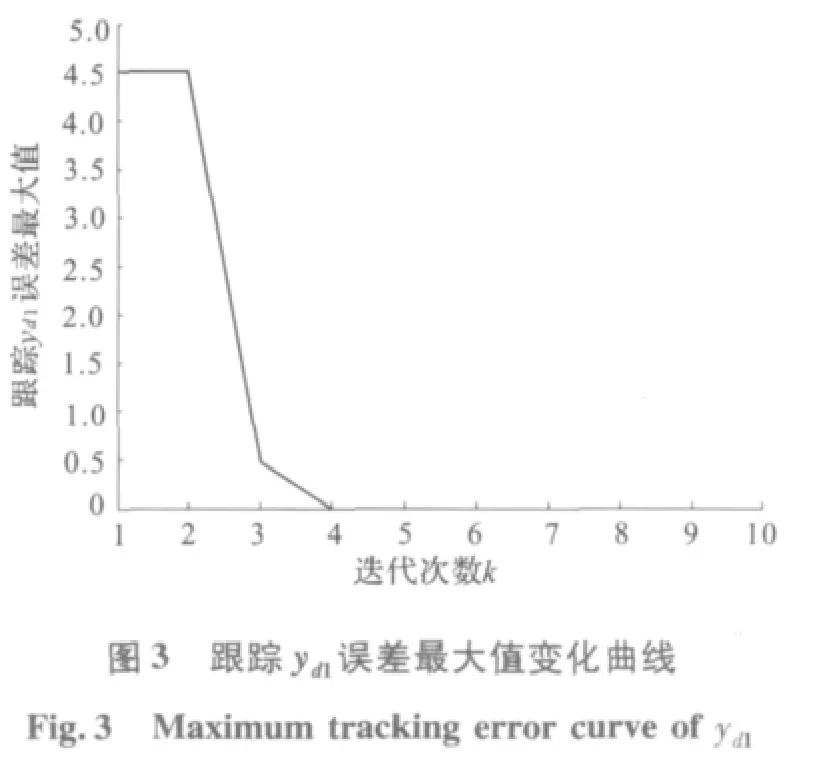
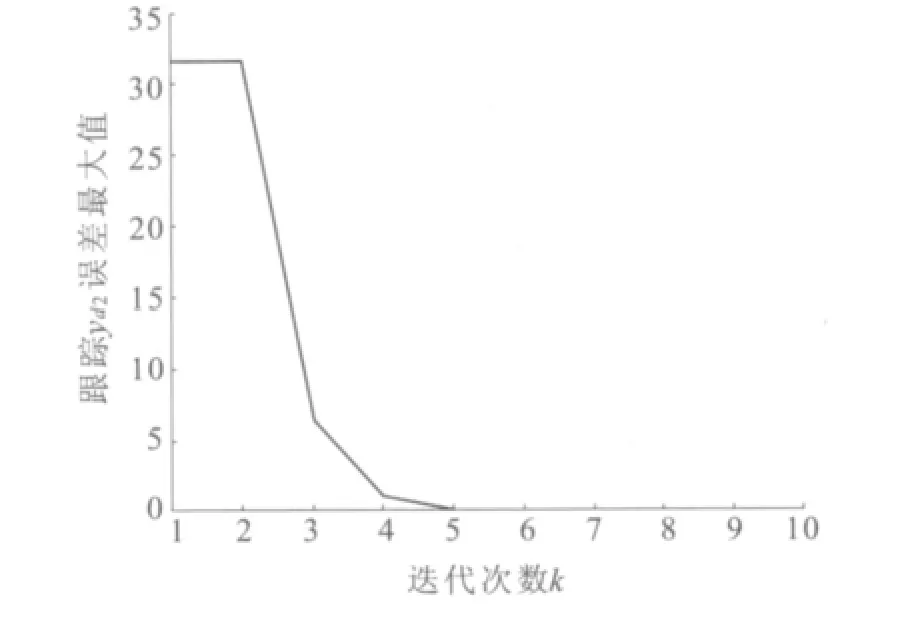
图4 跟踪yd2误差最大值变化曲线Fig．4 Maximum tracking error curve of yd2

4 结论

针对一般非线性离散系统结构、参数等很不确定而且非线性环节的存在使得系统控制器的研究变得复杂的特点，在充分利用系统上次和当前运行得到的信息及闭环控制效果要优于开环的结论的条件下，本文给出了对于一般非线性离散系统的开闭环P-D 型迭代学习收敛的充分条件，仿真结果表明了该充分条件的正确性。

［1］谢振东，刘永清．分布参数系统目标跟踪的二阶P －型学习 算 法［J］．暨 南 大 学 学 报，1998，19 (1):60-64．Xie Zhendong，Liu Yongqing．Two order p-type learning control algorithm of distributed parameter systems ［J］．Journal of Jinan University ［J］.1998，19 (1):60-64．

［2］田森平，谢胜利，傅予力．连续非线性系统的迭代学习控制 算 法［J］．中 山 大 学 学 报，2000，39 (6):313-317．Tian Senping，Xie Shengli，Fu Yuli．Iterative learning control algorithms for nonlinear continuous systems ［J］．Acta Scientlarum Naturalium Universitatis Sunyatseni，2000，39(6):313-317．

［3］谢胜利，谢振东，田森平．非线性系统的迭代学习控制及其算法实现［J］．控制理论与应用，2002，19 (2):167-172，177．Xie Shengli，Xie Zhendong，Tian Senping．Iterative learning control and algorithm realization of nonlinear systems［J］．Control Theory ＆ Applications，2002，19(2):167-172，177．

［4］Tayebi A，Zaremba M B．Iterative learning control for nonlinear systems described by a blended multiple model representation ［J］．International Journal of Control，2002，75(16):1376-1384．

［5］谢振东，谢胜利，韦岗．非线性学习控制理论及其在机器人系统上的应用［A］．中国控制会议论文集［C］．北京:国防大学出版社，1998．957-961．Xie Zhendong，Xie Shengli，Wei Gang．Nonlinear learning control theory and its application on the robot system ［A］．Paper Collection Chinese Control Conference ［C］．Beijing:National Defense University Press，1998．957-961．

［6］李洋，谷俊杰，支保峰，等．加权闭环PD 型迭代学习控制在重复扰动时的应用［J］．电力科学与工程，2008，24 (1):48-50．Li Yang，Gu Junjie，Zhi Baofeng，et al．Application of the weighted PD-type closed-loop iterative learning control in the repeated disturbances ［J］．Electric Power Science and Engineering，2008，24 (1):48-50．

［7］Tian Senping，Xie Shengli．A nonlinear algorithm of iterative learning control based on vector plots analysis ［C］．Wuhan:Procceedings of the Second International Symposium on Intelligent and Complex Systems，2001.17-20．

［8］田森平，谢胜利，傅予力．一种新的迭代学习控制快速算法［J］．华 南 理 工 大 学 学 报，2002，30 (5):37-40．Tian Senping，Xie Shengli，Fu Yuli．Fast algorithm of iterative learning control ［J］．Journal of South China University of Technology，2002，30 (5):37-40．

［9］Qu Z．An iterative learning algorithm for boundary control of a stretched moving string ［J］．Automatica，2002，38(5):821-827.

［10］Xie Shengli，Tian Senping．A fast algorithm of iterative learning control based on the geometric analysis［C］.Xiamen:Proceedings of the 2002 International Conference on Control Theory and Automation，2002. 472-476.

［11］谢胜利，田森平，谢振东．基于几何分析的迭代学习控制快速算法［J］．控制理论与应用，2003，20 (3):419-422.Xie Shengli，Tian Senping，Xie Zhendong．Fast algorithm of iterative learning control based on geometric analysis［J］．Control Theory ＆ Applications，2003，20 (3):419-422．

［12］史忠科．非线性离散系统的迭代学习控制方法及其应用［J］．控制理论与应用，1998，15 (3):327-332 Shi Zhongke．Iterative learning control method for nonlinear discrete-time systems ［J］．Control Theory ＆ Applications，1998，15 (3):327-332．

［13］曾南，应行仁．非线性系统迭代学习算法［J］．自动化学报，1992，18 (2):168-176．Zeng Nan，Ying Xingren．Iterative learning control algorithm for linear dynamical system ［J］．Acta Automatica Sinica，1992，18 (2):168-176．

［14］高卫华，谢剑英．一般非线性离散系统的闭环迭代学习控制研究［J］．系统仿真学报，2001，13 (1):73-74，109．Gao Weihua，Xie Jianying.Closed-loop iterative learning control for general nonlinear discrete system ［J］．Journal of System Simulation，2001，13 (1):73-74，109．