城市综合承载力评价研究——基于三角模糊层次分析法
○ 徐 骁 赵富强 李东序
(武汉理工大学管理学院 湖北 武汉 430070)
城市可持续发展是在经济、社会、环境等能够自我调节和自我恢复的阈值范围内的可持续发展,城市发展的阈值就是城市承载力,这个阈值会随着时间推移、科技进步以及行为方式和价值观念等的不断改变而发生变化。当今世界,城市化在给现代城市带来繁荣的同时,也使其面临前所未有的承载压力,故提升城市综合承载力、实现可持续发展已成为人类共同的战略需求。
一、城市综合承载力评价模型构建
1、城市综合承载力的内涵界定
笔者认为,城市综合承载力即一定时期、一定区域和一定社会、经济、生态与科技条件下,城市资源在自身功能完全发挥时所能持续承载的城市人口各种活动规模和强度的阈值。城市综合承载力包括两方面的含义:一是对载体而言,城市不仅包括硬件,而且包含文化、政策、制度、精神、管理、开放等软件;二是对承载对象而言,由于城市发展的目标是使人类社会经济活动与环境相协调,所以承载对象是人类的各种社会经济活动,如人口规模、经济产值、交通规模、纳污能力等。因此,城市综合承载力是社会、经济、环境协调程度的表征。
2、城市综合承载力弓弦箭模型
笔者认为城市承载力是个复杂的系统,其众多要素和子系统以不同方式存在,共同耦合构成城市综合承载力,从而支撑城市人口社会经济活动的协调发展。根据城市综合承载力内涵,结合城市发展实际,借鉴城市发展相关理论,特构建城市综合承载力评价模型,即城市综合承载力力=F(硬件承载力,软件承载力,软硬结合力);硬件承载力=环境承载力+土地承载力+设施承载力+水源承载力+能源承载力;软件承载力=文化承载力+制度承载力+管理承载力+科技承载力+学习承载力+开放承载力;软硬结合力=产业承载力。

表1 城市硬件要素承载指数界定

表2 城市硬件要素承载状态划分

表3 城市软件要素承载指数界定

表4 城市软件要素承载状态划分
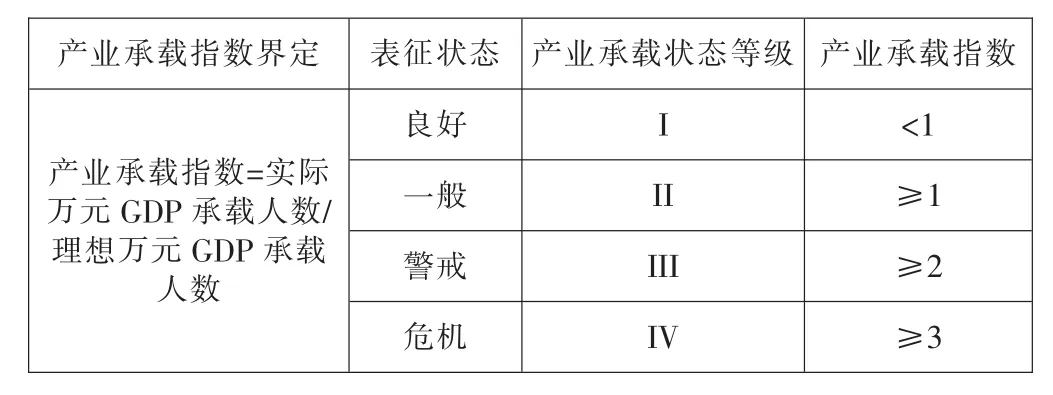
表5 城市软硬结合要素承载指数界定及状态划分
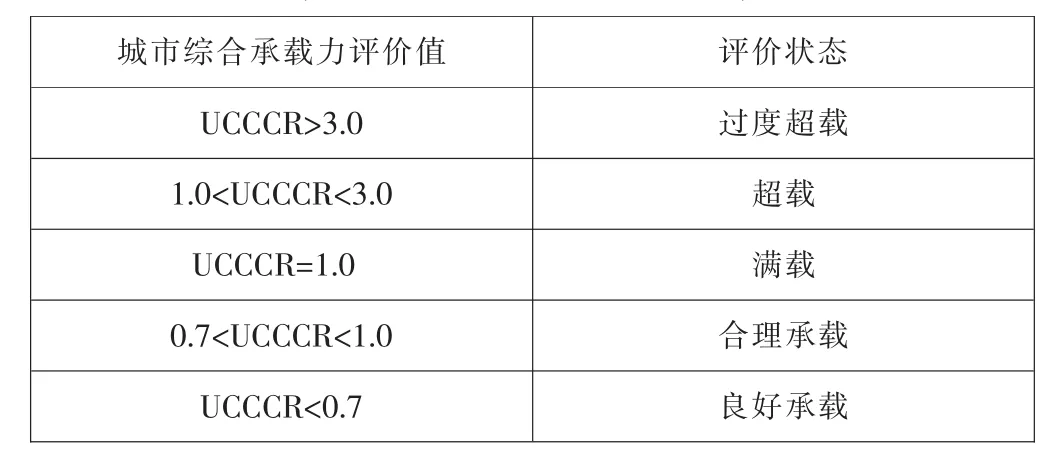
表6 城市综合承载力判别表
二、城市综合承载力评价指标设计
由于城市综合承载力的测度是个相对量,故用承载指数衡量。承载指数是通过现有要素承载力水平与预警性指标比较而得出的城市承载力,其中预警性指标是指要素承载能力的警戒标准。如现有要素承载力数值大于预警性指标,则承载力负荷较大,潜在承载力发展空间较小,城市发展受限,城市就会出现问题;如要素承载力数值小于预警性指标,则城市承载力发展有一定空间;如要素承载力数值等于预警性指标,那么城市承载力空间等于零。承载状态与承载指数保持一致,即承载指数越高,承载状态越好。根据承载指数情况,可将承载状态分为良好、一般、预警和危机等状态。硬件要素承载指数界定如表1所示,硬件要素承载状态的划分如表2所示,软件要素承载指数界定如表3所示,软件要素承载状态的划分如表4所示,软硬结合力承载指数界定和承载状态如表5所示。
三、城市综合承载力评价方法选择
1、TFAHP的方法提出
由于客观事物的复杂性和人们对事物认识的模糊性,因此在两两权重比较赋值上,把本来就模糊的量明显化显然是不合适的。1983年荷兰学者Van Laargoven提出用三角模糊数表示Fuzzy比较判断的方法,并运用三角模糊数的运算和对数最小二乘法求得元素排序,即用三角模糊数M(l,m,u)来表示AHP中两两比较判断矩阵中的重要性值,其中m为专家判断的最可能值,l与u则为m的两个上下边界,可理解为最悲观值与最乐观值。显然,当l=m=u时,M退化成一个实数。TFAHP的一般步骤:首先,构造模糊判断矩阵;其次,进行一致性检验;再次,计算综合层次度;最后,进行层次排序。
AHP方法定性与定量结合的特点,使其非常适合粗略的城市承载要素量化与分析工作。根据城市综合承载力特点,充分尊重决策的模糊性,采用TFAHP法对城市综合承载力要素进行量化分析和选择判断。在构建判断矩阵时采用三角模糊数,并在一致性判断时采用近似计算方法,得出要素权重大小可能性程度后按相关公式进行排序,最终得出各承载要素指标的权重排序。从应用效果看,该方法在主观量化分析领域有较强实用价值。
2、TFAHP的应用原理
(1)三角模糊数的定义。人们在处理复杂的决策问题,进行选择和判断时都会不自觉地使用模糊判断。三角模糊数模型考虑到这一特点,利用三个元素来表示一项判断的准确性,即设有因素X={x1,x2,…,xn},在模糊比较判断时,因素xi比因素xj明显重要,可用三角模糊数 rij=(l,m,u)表示,其中左右扩展 l、u表示判断的模糊程度。当u-l越大时,则比较判断的模糊程度越高;当u-l=0时,则l,m,u判断是非模糊的,rij为一实数。当给出个模糊判断后,可得到由三角模糊数组成的模糊判断矩阵R={rij}n×n。
(2)构建三角模糊判断矩阵。根据总体目标要求,通过两两比较得到评价准则的模糊判断矩阵,记为:

式(1)中n为评价准则个数。
当ri比rj重要时,令rij=(lij,mij,uij),其是一个三角模糊数,lij和uij为其上下界,mij为两个判别准则的重要性数字量度,其值应该在 1 和 9 之间。当 ri比 rj重要时,令 α=mij-lij,β=uij-mij。当ri没有 rj重要时,令 α=mji-lji,β=uji-mji。当 0<α,β<1/2,模糊度过小,无法完全反映人们认识的模糊性。当α,β>1,模糊度过大,置信度减小。实践结果表明,当1/2<α,β<1时结果比较理想。我们可以通过模糊判断矩阵获得其模糊互补矩阵。
(3)计算评价准则的综合重要程度值。称xi对其他因素的模糊综合程度为:

aij≥akj的可能性程度为K(aij≥akj):

(4)计算评价准则的归一化权重值。将三角模糊数aij大于m个三角模糊数akj(k≠i,k=1,2,…,m)的可能性程度定义为:
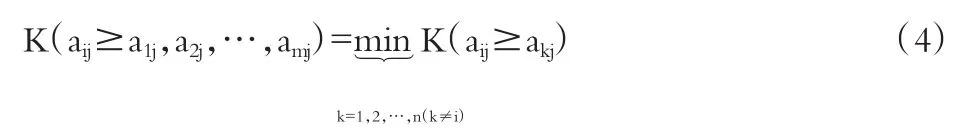
d(xi)为xi与其他因素比较的综合重要程度,即:

则权重 W=(d(X1),d(X2),…,d(Xn)),归一化得 W1=(d1(X1),d1(X2),…,d1(Xn))。
(5)计算总体目标评价值。将每个评价准则进行分级,每一等级都有一个分数范围,整个分数范围为0—100。计算得分时,首先确定某个评价准则的等级范围,再根据等级范围的分数上下界计算出该准则的得分。假设某次评价时,针对评价准则Ci的得分为Pi,可得到总体目标的评价值:

四、和谐视角下城市经营绩效状态判别
1、城市综合承载力理论模型
城市综合承载力是一定条件下能够支持城市人类社会经济活动的综合利用阈值。因此,城市综合承载力可以表示为:UCCC=F(H,S,I),其中 H 为硬件承载力变量,S 为软件承载力变量,I为软硬承载结合力变量。H=F(e,l,f,w,r),其中 e 为环境承载力变量,l为土地承载力变量,f为设施承载力变量,w为水源承载力变量,r为能源承载力变量。S=F(c,p,m,t,s,o),其中c表示城市文化承载力变量,p表示制度承载力变量,m表示管理承载力变量,t表示科技承载力变量,s表示学习承载力变量,o表示开放承载力变量。软件承载力不能独立对城市综合承载力起作用,只能通过与硬件承载力有机融合才能充分发挥其作用。I=F(i),其中i为产业承载力变量。
2、城市综合承载力计量模型
3、城市综合承载力判别
根据承载力的计算值城市综合承载力可分为:过度超载,城市承载要素己受到严重破坏或对干扰的调控能力很弱,自动恢复很难甚至已无自动恢复能力,部分承载功能己丧失;超载,城市承载要素已受到破坏或对干扰的调控能力弱,自动恢复难;满载,城市承载要素己处承载临界点,城市承载要素生产力已被全部利用,对干扰的调控能力一般,自动恢复能力不佳;合理承载,城市承载要素受人为不合理影响较小,对干扰的调控能力较强,自动恢复能力较快;良好承载,城市承载要素受人为不合理影响很小,对干扰的调控能力强,自动恢复能力快,环境生产支持力强。根据专家德尔菲法,结合不同城市实际和以往评价分级标准,在考虑各承载力权重的基础上,对城市综合承载力评价采用5级分法如表6所示。
[1]李涛:城市规划在城市和谐构建中的地位[J].中华建设,2008(4).
[2]闵庆文、余为东、张建新:区域水资源承载力的模糊综合评价分析方法及应用[J].水土保持研究,2004(3).
[3]Rees W E.Revisiting Carrying Capacity:Area Based indicators of Sustainability[J].Population and Environment,1996(3).
[4]程枫、廖建新、朱晓民等:基于三角模糊数层次分析法的彩铃业务服务质量评价[J].重庆邮电大学学报(自然科学版),2008(1).
[5]徐泽水:三角模糊数互补判断矩阵排序方法研究[J].系统工程学报,2004(4).

