利用基于密度函数的随机模拟滤波测算流通中的货币量

○ 李洪雨 曹 莉 顾维清

（重庆大学数学与统计学院 重庆 401331）

一、引言

众所周知，适度的流通中货币量有利于经济发展，而货币流通速度可以告诉我们货币政策能否有效地引起经济扩展。Hudson B.Hastings（1923）曾为它们定义：流通中的货币量是通货和某一时期由个人、协会、政府机构立即支付的银行存款的和；货币流通速度是在某一时间段内流通中用来消费的每一分货币的平均周转次数。

Irving Fisher（1909）是第一位用定量分析法来计算速度，并间接估计流通中的货币量依赖从非存款人（主要是未被统计的工资领取者）中流入银行与流出银行的货币量的和，流通速度等于上面的和除以流通中的货币量。同时，教授Fisher指出在他这篇文章中有误差较小。但是，David Kinley（1910）认为改进后的存款估计值有可能会很大而且对在农业和国内其他行业的工作人员的薪水很难得到可靠的估计。John P.Gould and Charles R.Nelson（1974）收集了观察到的速度根据随机游走模型来预测未来的速度，但是他只是单独地关注速度这一变量而没参考其他的经济变量。结果是大部分人对这种方法的可信度持很深的怀疑态度。

B.B.Dunaev（2010）提出真实的货币流通量等于M1和货币平减指数的比值，与投入到生产领域的成本成比例，货币流通速度则等于名义GDP与M1的比值。另外，他指出货币投放只能在短期内缓解市场上货币的不足，随着价格增加，流通中货币数量又变回投放前的数量。与此同时，大部分中国学者常利用货币供应量的划分和货币数量论作为理论依据来测量速度。实际上，大部分研究仅限于速度的测量，主要是针对M0、M1、M2相对应的速度的计算和分析。但是，在本文中我们将抛开这些划分，构建经济模型来计算货币流通量和相应的速度。

Irving Fisher（1909）提出在相同时间内容器中水的净流出量一定等于容器中的净减少量这一原理，为我们提供了可靠的理论基础。并且，货币流出量与流入量是调节经济的重要手段。结合货币流通量，三者形成了动态变化。我们可以从本质上描述这种动态变化：某一季度的货币流通量等于这一季度的流出量与流入量的差值和前一季度的货币流通量的和。基于这样的变化，我们可以考虑状态空间模型。因为流通中的货币流通量是不能观察到的，所以我们选择基于密度函数的随机模拟滤波来测量流通中的货币量。Tanizaki，H.（1996）详细地描述了这种可以最大减少估计量误差的方法。这种方法的目标是数据点出现时，它能更新状态变量的信息。然后，考虑到最大化，我们利用最大似然函数的方法来获取流通速度的最优值。通过处理近十年的数据，我们得出了有意义的结论：计算的货币流通量能较好地解释CPI的变化。

p（z1｜z0）=p（z1），Zt=｛z1，z2，…，zt｝，即Zt包含了t时刻的所有信息。已知Mt在给定Zt-1条件下的条件分布和新数据Zt+1，我们想求出Mt+1在Zt条件下的条件分布，这就是基于密度函数的随机模拟滤波。

从等式（1）可知，zt｜Zt-1是独立同分布的随机变量且zt｜Zt-1～N（μt｜t-1，σ2t｜t-1），μt｜t-1=vMt｜t-1，σ2t｜t-1=σ2w，Mt｜t-1=E[Mt｜Zt-1]。

我们只有求出Mt｜t-1才能得到上面的似然函数，接下来我们将分两步来求。

先求Mt｜Zt-1的密度函数：

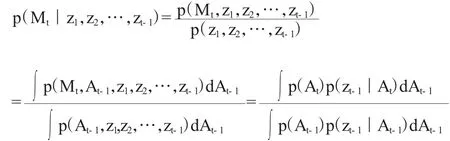
二、状态空间模型

因为货币流通量的流动性较强，所以在本文中我们只考虑现金这一形式。我们现以季度为一个计时点，定义货币流出量为每季度从银行流进市场上的新贷款，如商业贷款、工业贷款、外汇占款；定义货币流入量为每季度从市场流入银行的新存款，如个人储蓄存款、商业存款。

状态方程：Mt=Mt-1-Dt+Lt+ut。

Mt是在时刻t的货币流通量且不能观察到的，Dt是在时刻t的货币流入量，Lt是时刻t的货币流出量，ut是扰动项且独立同分布，服从均值为0，方差为σ2u的随机变量。

转变方程：PtYt=vMt+wt。

令 zt=PtYt，就有：

zt是GDP与物价指数在时刻t的乘积，wt是扰动项且独立同分布，服从均值为0，方差为σ2w的随机变量。

在这两方程中，Dt，Lt，zt均为可观察变量，而Mt为所求变量。我们这篇文章主要目的就是求出t时刻的货币流通量（即Mt）及此时刻的流通速度v。因为Mt是不能观察到的，所以我们选择用基于密度函数的随机模拟滤波来测量Mt。这种方法的目标：当获得一个新的数据点时递归地更新状态变量的信息。

考虑zt的似然函数：

记At=｛m1，m2，…，mt｝。

再利用Mt｜Zt-1的密度函数来求Mt｜Zt-1的期望：

我们可以利用模拟轨道来得到期望的样本形式：

其中，mj，t为第j条轨道上的mt，Aj，t=｛mj，1，mj，2，…，mj，t｝。

得到：

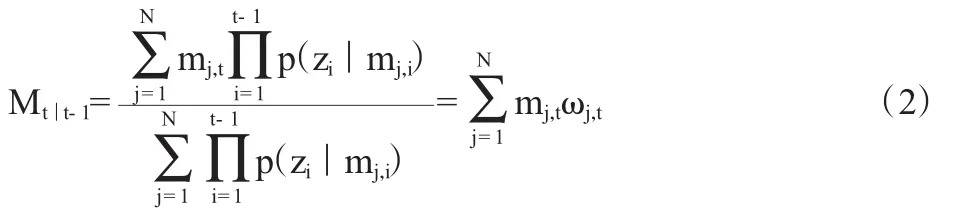
ωj，t=我们得到ωj，t的递推公式。

其中，zt｜mj，t～N（vMj，t，σ2w），我们知道它的密度函数。

p（Zt｜Mj，t）=，我们的目的是要求出z1，z2，…，zn的联合密度函数：

p（z1，z2，…，zn），而 Mt｜t-1可以由（2）求得，所以联合密度函数也可求出。根据滤波方法的思想，当密度函数的对数取最大值时，求出相对应的v及Mt｜t-1。

三、实证分析

首先，我们从国家统计局收集了1999年第一季度到2010年第三季度的GDP和CPI数据，从人民银行每月公布的金融机构信贷收支表中选取了每月的货币投放量（各项贷款和外汇占款）和货币回笼量（各项存款），并通过求和转为季度的。其次，我们利用Matlab软件计算出流通速度v=36.98和每季度的流通量 Mt｜t-1，如图 1 所示。

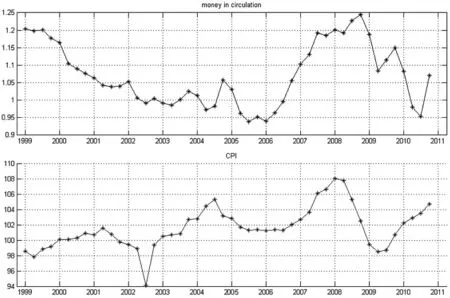
图1 流通速度和每季度的流通量

我们结合中国人民银行每季度公布的《货币政策执行报告栏目》来探讨这个结论。从1999年第二季度开始，货币回笼量与货币投放量之间的差值持续变大，市场上流通的货币量在下降，CPI在上升，到了2001年第二季度，CPI上升到最高点。随着货币紧缩的加剧，从2001年第三季度开始，CPI显著下降。2002年到2003年，流动性继续紧缩，CPI在2002年第三季度降到历史最低点。2004年4月份央行上调了法定存款准备金率，流通性紧缩，后两季度贷款增量稳步回升，新增贷款结构进一步改善，流通中的货币出现了先少后多。2005年前三季度，金融机构存款较快增长，流通性紧缩，市场上流通的货币呈减少趋势。2004年到2005年的CPI也出现了先上后降的趋势。2006到2007年，货币投放量与货币回笼量之间的差值持续变大，市场上的货币量在持续增加，CPI也出现递增的趋势，在2008年的第一季度上升到了最高。2008年前两季度央行4次上调存款类金融机构存款准备金率，流通中的货币量减少，而后两季度央行3次下调存款类金融机构存款准备金率，流通中的货币量增加。2009年前两季度，美国2008年次贷危机对中国的影响开始显现出来，从2008年第四季度到2009年的第二季度，流通中的货币量一直在减少，CPI也一直减少并在2009年第二季度降到最低。2009年，为应对经济危机，保证经济的平稳运行，银行降低了存贷款利率，金融机构贷款的增速较快，在后两季度流通中的货币量开始增加，CPI也出现上升。2010年，前两季度央行3次上调存款类金融机构存款准备金率，货币回笼量增加，市场上的货币量减少，但是CPI从2009年第二季度就持续上升，这一种现象可能有两种原因：一是政策的效果还没有显现，还需要后来的数据；二是仅有货币政策还不够，还需要有其他政策辅助。

四、结论

本文利用基于密度函数的模拟随机滤波测算了流通中的货币量和流通速度。在模型中，我们详细地推导了GDP和CPI乘积的似然函数以及货币流通量在它的条件分布下的期望。我们得到过去近十年每一季度的货币流通量，并与CPI进行了较为详尽的对比。对比表明货币流通量的多少对CPI的变动起了一定的影响作用。换句话说，调节流通中的货币量对控制物价上涨有一定的帮助，当然，我们还需要其他的货币政策，如利率，期望得到通货膨胀率，所要巩固的经济效率等。要想获得准确的经济效果，我们必须考虑更多的经济因素。本文的不足之处就是在建立模型时，我们一开始就假定扰动项是独立同分布的随机变量。不管怎样，我们期盼对货币供应量有更多的研究。

[1]B.B.Dunaev：Money supply and interest rate in economic equilibrium [J].Cyberneticand SystemsAnalysis,2010，46（1）.

[2]Hudson B.Hastings：The Circuit Velocity of Money[J].The American Economic Review，1923,13（2）.

[3]David Kinley：Professor Fisher's Formula for Estimating theVelocity oftheCirculation of Money[J].Publications of the American Statistical Association，1910,12（89）.

[4]John P.Gould and Charles R.Nelson：The Stochastic Structure of the Velocity of Money[J].The American Economic Review，1974，64（3）.

[5]Irving Fisher：A Practical Method of Estimating the Velocity of Circulation of Money[J].Journal of the Royal Statistical Society，1909,72（3）.