一种基于交通视频的摄像机标定方法

朱小平，付洋

（长安大学 信息工程学院，陕西 西安 710064）

视频检测技术在交通信息检测中有着重要的应用，主要利用图像处理技术对获取到的交通视频图像进行一系列处理，提取出有用的信息，完成交通参数、交通状况和交通事件的检测，是 ITS（Intelligent Transportation System）中的一个热点研究方向。视频检测技术在摄影测量、计算机视觉等领域的应用，一个基本的问题是摄像机的标定问题。在实际的图像视频处理中为确定实际空间物体的三维坐标与图像上的对应点的映射关系，需要通过建立相应的几何模型，求解几何模型的参数，几何模型的参数就是摄像机参数，这个参数的求解过程称为摄像机的标定[1]。在视频检测技术中，摄像机的标定是最基础的和最重要的一步，它的精度和准确度直接影响后续工作的结果。因此提高摄像机标定的准确度和算法的简洁度是研究工作的重点所在。

摄像机的标定可以采取在特定的试验条件下，基于形状、尺寸已知的参照物，利用图像变换和数学计算的方法来获得摄像机的参数，称为传统的摄像机标定方法。此类标定方法大体有以下几种：利用最优化算法的标定方法，典型代表有摄影测量学中的传统方法和线性变换法，这两种方法是由Faig在文献[2]和A bdel-Aziz在文献[3]中提出；利用摄像机变换矩阵的标定方法[4]；考虑畸变补偿的两步法[5]；双平面方法[6]；改进的张正友标定法[2]等。这些方法利用特定的参照物获得实际空间物体与图像上对应点的映射关系，算法简单，但有一定的试验条件要求。

此外还可以采取不依赖参照物，利用不同帧图像上物体之间的对应关系的方法进行标定，即自标定方法。主要有利用绝对二次曲线和极线变换性质解Kruppa方程的摄像机自标定方法[8]；基于二次曲面的自标定方法[9]；基于主动视觉的摄像机自标定技术[10]等。此类方法灵活实用，但精度有待进一步提高。

在以前这些方法的基础上，现在有很多改进的方法，例如一种利用Hough变换提取矩形棋盘格的角点，求出摄像机参数初始值，运用Levenberg-Marquardt算法对初始解进行非线性迭代优化[11]。一种以渐变圆形为特征的摄像机标定模板的检测算法[12]等。针对上述方法的特点，本文是在交通视频检测技术的实际应用中提出的摄像机标定问题，可以利用路面上标线作为参照物，提供一种线性模型下的摄像机几何标定方法，该方法根据摄像机成像原理抽象出几何模型，推算出图像像素段变化时对应的路面实际距离变化的函数关系式，从而建立视频图像像素行与路面实际距离的映射关系，然后采取多级求解的方法减小误差，采用该方法不用考虑摄像机内部参数，几何推导出外部参数，该方法简单易行，计算量小。

1 标定方法

1.1 建立几何模型

由公路路面上架设的摄像机采集到的视频原图像为基准，手动画定至少3个点（文中选择3个点进行说明），这些点的选取的条件是它们之间的距离在实际路面上是相等的。如图1所示，3个点形成两个像素段m和n，它们在实际路面上的距离是相等的。取n段的下端点分别向下和上延伸代表图像上的像素段的变化，同样的取m的上端点分别向下和上延伸代表图像上的像素段的变化（如图1中的L）。

图1 参照物的选取Fig.1 Selection of reference

依据图像变换的基础知识再结合摄像机成像的原理抽象出图像上像素距离与实际路面的距离之间的几何模型，抽象出的几何模型如图2所示，其中①②③④代表视频图像上的4个不同的求解区域；m，n表示视频图像上的两个像素段，这两个像素段对应的实际距离相等，假设都是A；在区域①里，L表示在视频图像上以n的下端点为基准向下延伸的像素段；在区域②里，L表示在视频图像上以n的下端点为基准向上延伸的像素段；在区域③里，L表示在视频图像上以m的上端点为基准向下延伸的像素段；在区域④里，L表示在视频图像上以m的上端点为基准向上延伸的像素段；K代表当L移动时对应的路面实际距离的变化量。如图2可以清楚地看到m、n所代表的路面实际距离相等，L变化的同时K也跟着做相应的变化，下面进行推导得到L和K的4个函数关系式。

1.2 一维标定算法的几何推导

如图3是一维标定算法的几何推导图。在视频上找一个点M，M点所对应的路面上的点为N，关键问题是找出视频图像中像素距离MD所对应的实际距离NA。其中O点是摄像机的焦点，最下面的一条线（NC）是实际路面中的车道线，上面一条（MF）是摄像机拍摄的交通视频图像中对应的车道线，4 条斜竖线（ON、OA、OB、OC）是摄像机光线，D、E、F 是选择的3个点，n=DE，m=EF，它们对应的实际路面分别是AB和BC，其中 AB=BC=h。做两条辅助线：AG和NH，且AG和NH分别平行于MF。

已知条件为：

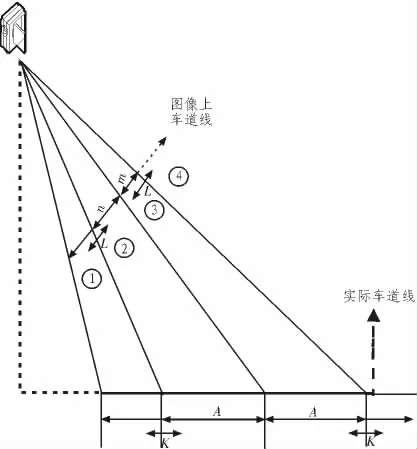
图2 几何模型Fig.2 Geometric model

DE、EF和 MD像素距离已知；AB=BC，并且都已知；MF∥NH∥AG（∥表示平行，△表示三角形，～表示相似）。求NA的实际距离。

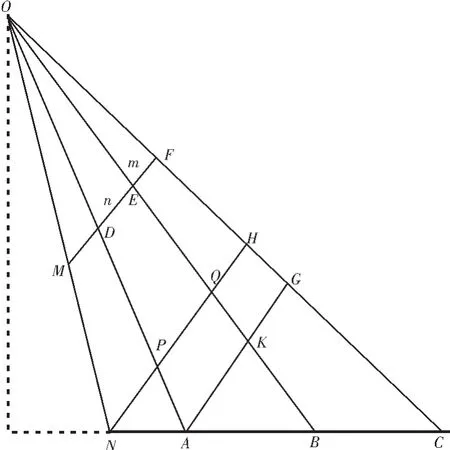
图3 几何推导图Fig.3 Fig of the geometric derivation

求解过程如下：

对于①区域的求取：

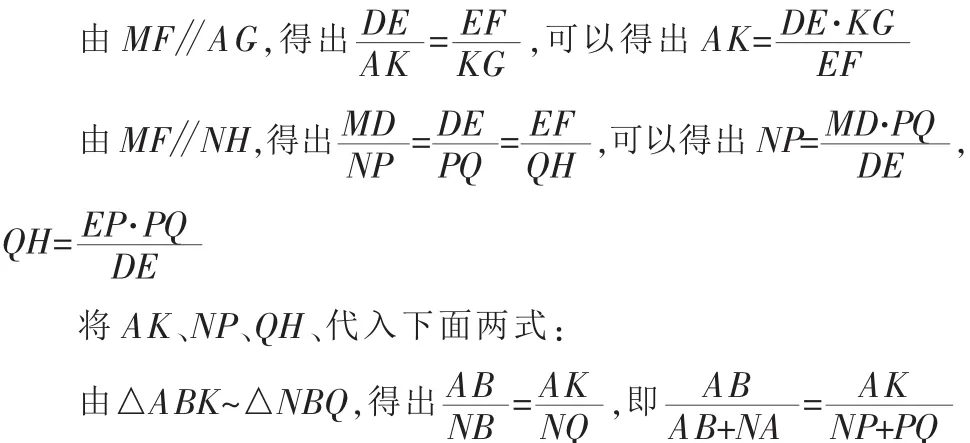
1.3 算法结果分析

下面对这4个公式进行分析，它们都符合一个函数模式，即：

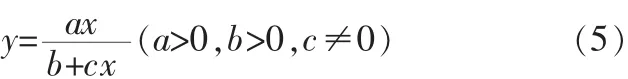
式（5）可以变形为：

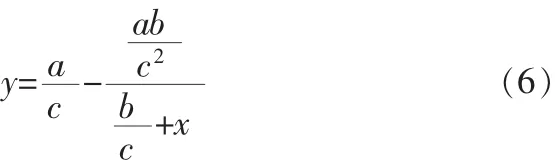
当 c＞0 时，式（6）的函数如图 4（a）所示，当 c＜0 时，式（6）的函数如图 4（b）所示。 由图 4 可见，式（6）的函数根据 a、b、c的不同有极值，所以x不能无限地增大或减小，如果无限地增大或减小x实际求得的值可能和真实情况不相符。

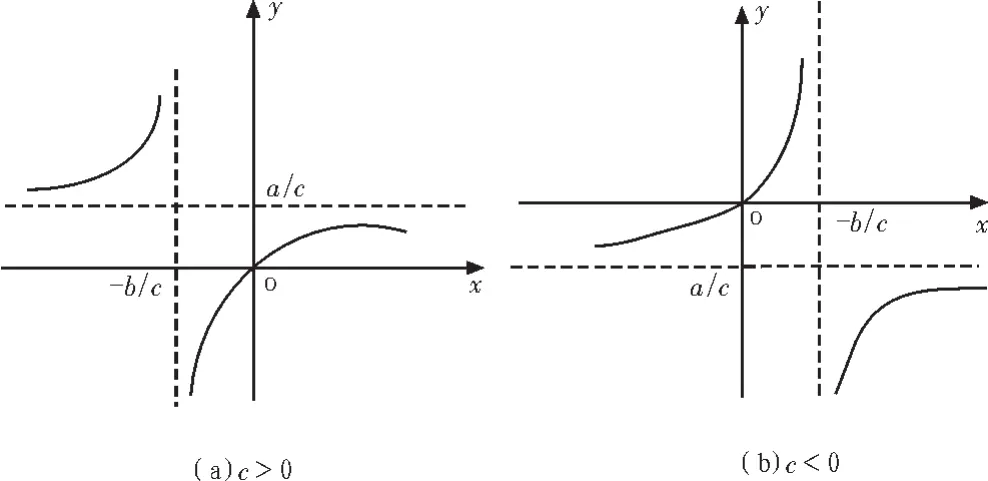
图4 （4）式函数Fig.4 Function image of（4）

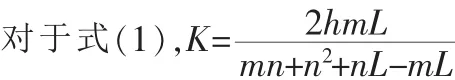
a=2hm，b=mn+n·n，c=n－m，c＞0，a/c=2hm/（n－m）， 若 m＜=n/3，则 a/c＜=h，若 m＞n/3，a/c＞h，一般情况下 m＞n/3，所以 a/c＞h，当 L=n（m+n）/（3m－n）时，K=h。所以在区域①里 L 的取值范围是（0，∞），函数是单调递增的，函数值 K的范围是（0，2hm/（n－m））。

同理可以分析式（2）、（3）和式（4），这里省略。 由此可见，如果只把一整幅视频图像划分为4个区域，如图2所示，那么有可能区域①的范围过大，当区域①的实际距离大于 a/c=2hm/（n－m）时，这时候用式（1）求解的结果有一定的误差，因此实际应用时将一整幅图像划分为多个递推的四区域如图5所示，以减少这些因为函数的极限问题带来的误差。

图5 多个四区域标示Fig.5 More than four labeling

2 试验结果分析

在Visual C++6.0集成开发环境上进行软件的编程实现上述的算法，得到试验结果如下。

参看图6，手动定位图像上的14个点生成和分析映射关系。点0到点6，这7个点相邻两个点之间的实际距离都等于1 500 cm，点7到13这7个点之间的距离也是1 500 cm。（其中7到13为生成映射表所用的点，0到6为分析映射表误差所使用的点）。

图6 试验标定图Fig.6 Diagram of the test calibration

下面所列为0到6这7个点y方向的值，也就是像素的行值。实验数据如表1所示。

将整个图像分为一个四区域求解基本的行到距离的映射表（实验使用 11，12，13这 3个点生成），那么图 6中手动定位的7个点在映射表中的映射距离值如表2所示（temp[]表示对应于图像上的每一行的实际距离，单位是cm）。

表1 手动定位的点Tab.1 Point of the manual position

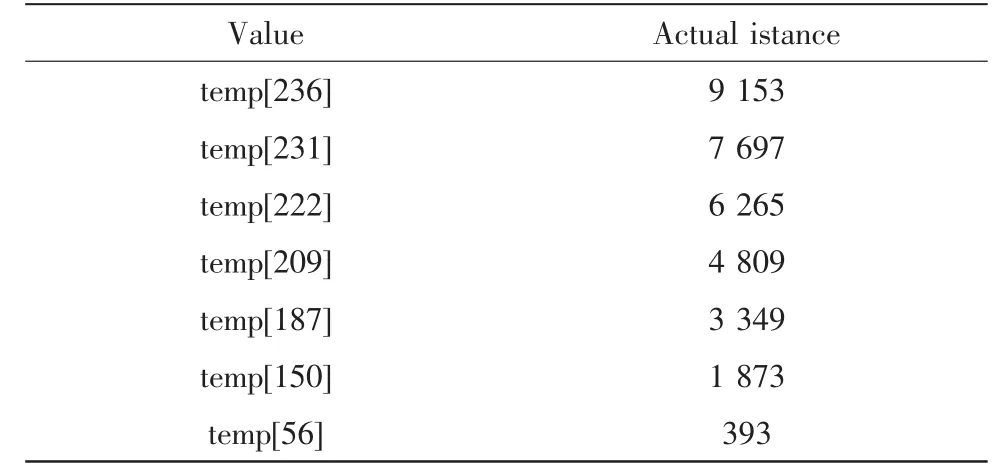
表2 行到距离的映射表中的7个点值（一个四区域）Tab.2 Seven point value of line to distance in the mapping table（a four regional）

若采用多点递推，利用点7到点13将整幅图像划分为多个四区域的temp表示图像上每一行的实际距离，单位是cm，如表3所示。

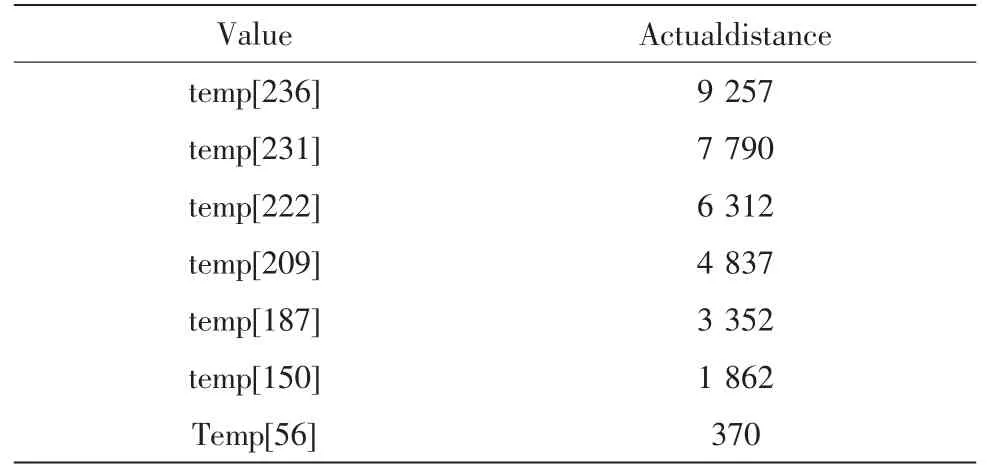
表3 行到距离的映射表中的7个点值（多个四区域）Tab.3 Seven point value of line to distance in the mapping table（more than four regional）

下面用手动确定的这几个点对这两种结果进行比较和误差说明:令 X1=56，X2=150，X3=187，X4=209，X5=222，X6=231，X7=236，Y（n）=|1 500－（temp[X（n+1）]－temp[X（n）]）|，Y 表示手动确定的7个点之间的差值与理想值（1 500）之间的差值（其中n=1，2，3，4，5，6，单位为 cm），如图 7 所示，a 表示一个四区域的Y值与n的关系曲线，b表示多个四区域的Y值与n的曲线。

下面对两种情况下的方差进行计算，利用

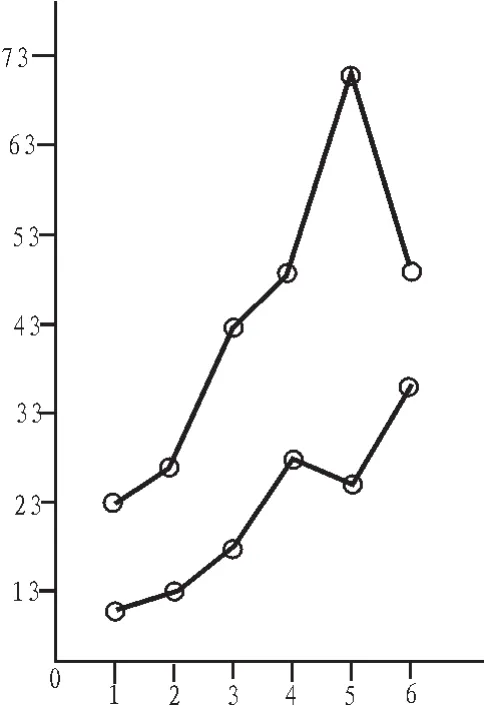
图7 对比图Fig.7 Comparison chart

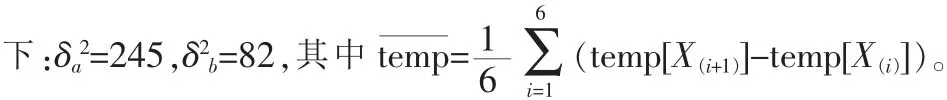
通过对图7的分析可以得到以下几点结论:

1）曲线b的值比曲线a的值小，即多个四区域的误差比一个四区域的误差小；

2）a、b曲线的值都大体呈现逐渐变大的趋势，即靠近摄像机的一边的误差小，远离摄像机的一边的误差大；

3）因为 δa2＞δ2b，得到多个四区域的结果的波动性小，精度更高。

综述实验结果可以看出靠近摄像机的一边的误差小，映射关系准确。曲线b的结果小，方差小，所以多个四区域得到的一维表的精度高，可以避免函数极限问题带来的很多误差。

3 结 论

文中讨论了一种线性模型下的摄像机标定方法，并对此进行了实际的试验，试验结果较为准确，能够实现图像上像素行到实际路面距离之间的转换关系，算法简单，计算量小，适用于视频交通系统中。在建立几何模型时采取的是线性变换，有一定的误差，在实际工程应用中进行了一些修正，影响不大，但是在需要高精度的条件下，还需要进一步的改进。

[1]马颂德，张正友.计算机视觉－理论与算法基础[M].北京:科学出版社，1998.

[2]Faig W.Calibration of close-range photogrammetric systems:mathematical formulation.photogrammetric eng[J].Remote Sensing，1975，41（12）:1479－1486.

[3]Abdel-Aziz Y I，Karara H M.Direct linear transformation into object space coordinates in Close-Range Photogrammetry[C]//Proc Symposium on Close-Range Photogrammetry，1971:1－18.

[4]Luh J Y，Klaasen J A.A three dimensional vision by off shelf system with multi-cameras[J].IEEE Trans PAMI，1985，7（1）:35－45.

[5]TsaiRY.Anefficientand accuratecameracalibrationtechnique for 3D machine vision[C]//Proc CVPR’1986:364－374.

[6]Martins H A，Birk J R，Kelley R B.Camera models based no data from two calibration planes[J].Computer Graphics and Imaging Processing，1981（17）:173－180.

[7]ZHANGZheng-you.A Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//Proceedings of 7th International Conferenceon Computer Vision，Corfu，1999:666－673.

[8]Moons T，Van GL，Proesmans M，et al.Affine reconst-ruction from perspective image pairs with a relative object-camera translation in between [J].IEEE Transaction on Pattern Analysisand Machine Intelligence，1996，18（1）:77－83.

[9]Triggs B.Auto-calibration and absolute quadric[J].Proceedings of Computer Vision and Pattern Recognition，1997:604－614.

[10]Ma SD.Aself-calibration technique for activevision system[J].IEEE Trans Robotics and Automation，1996，12（1）:114－120.

[11]孙杰，朱世强，赖小波.一种高效的视觉导航摄像机标定方法[J].计算机工程，2010，36（21）:212－216.SUN Jie，ZHU Shi-qiang，LAI Xiao-bo.An efficient visual navigation camera calibration [J].Computer Engineering，2010，36（21）:212－216.

[12]梁力，尹东斐，王川.高精度摄像机标定模板的设计及识别算法[J].西安交通大学学报，2011，45（4）:82－85.LIANG Li，YIN Dong-fei，WANG Chuan.Design and recognition algorithms of high-precision camera calibration template[J].Newspaper of Xi’an Jiaotong University，2011，45（4）:82－85.