钢构打字路径优化中旅行商问题的解决

刘 萍，高 军，丁筱玲

（1.山东信息职业技术学院 计算机系，山东 潍坊 261061；2.大庆油田电力集团 电力营销公司配网检修所，黑龙江 大庆 163451；3.山东农业大学 机械与电子工程学院，山东 泰安 271018）

随着经济的发展，各种机械产品的制造量大幅增加，产品信息标记的必要性和重要性愈加突出，铭牌成为机械产品信息的载体，而钢构打字亦渐渐成为国内外该行业的一个重要标志。钢结构打字技术即在要标识的钢件上用冲压动力冲击成型字模，冲压的字体清晰，深度容易控制，并且字头刀具寿命长，成本低。在该过程中，刀具路径的优化起着至关重要的作用，高效的刀具路径优化算法能够减少换刀次数和优化刀具移动轨迹，从而提高加工效率。刀具轨迹描述了加工过程中刀具和工件相对运动的具体位置与方式，包括有效的冲压运动轨迹和辅助运动轨迹；辅助运动轨迹主要用于刀塔转位、刀具定位等，虽不直接参与工件的成型，但却是加工中不可缺少的过程，需要花费一定的时间，因而对辅助运动轨迹进行优化极其必要。一般钢构打字属于多点位加工，由于辅助运动轨迹数量多，其排列顺序与加工路径的类型密切相关，用传统的路径量计算方法寻找最优路径非常困难。因此，该研究将工业钢构打字路径的优化问题抽象为基于旅行商问题（traveling salesman problem，TSP）的多项式数学模型。文中在深入研究当前刀具路径优化算法的基础上，提出应用遗传算法（genetic algorithm，GA）进行路径寻优的解决方案。

1 钢构打字路径寻优方案设计

由于数控机床加工中，换刀所用的时间相对于快速走刀时间要长很多，所以要提高加工速度，就要优先减少换刀次数。刀具路经优化一般需要考虑换刀次数、刀具移动的长度、加工时间、夹钳干涉等四方面因素。这里假定：不考虑机器故障以及刀具的磨损，机床最多只分配一把同一规格的刀具；同时，在生成数控代码的过程中，对字符加工的点位进行优化，尽可能缩短换刀、走刀路径，减少空行程的时间，以提高加工效率。基于上述原因，该组合优化系统采用一次换刀就不重复、不遗漏地加工完所有相同字符，再通过刀塔就近转位换刀加工其他字符的加工方式，这就存在如何安排字符的加工路线，从而使刀具空行程最少的问题。该文选择采用基于TSP的GA求解方法来规划辅助运动轨迹，以期从一个全新的角度探讨和研究关于工业钢构打字最优路径换刀技术问题。

2 路径寻优中TSP数学模型的建立

该文所涉及的钢构打字路径优化问题，可归结为带附加约束（即换刀次数最少）的旅行商问题（TSP）。TSP问题可描述为：一名商人欲到n个城市推销商品，如何选择一条路径使得商人经过每个城市一次且仅一次后回到出发点，并且所走的回路路径最短。TSP是一个典型的、易于描述却难于处理的问题，是许多领域内出现的多种复杂问题的集中概括和简化形式。它的数学模型可建立如下：

式（1）表示总行程最短；式（2）、（3）要求某人从 i货位出入货位j只有一次；式（4）约束机械手在任何一个货位子集中不形成圈；式（5）中Xij=1表示机械手选择从货位i到货位j的路线，Xij=0表示机械手不选择这条路线。设D=[dij]是货位距离的邻接矩阵，则表示货位i、j之间距离的元素dij具有以下特征：

1）非负性：dij≥0；1≤i；j≤n；

2）对称性：dij=dji；

3）对角线元素为 0：dij=0；

4）任意 3 个元素满足三角不等式：dij+djk≥dik，1≤i，j，k≤n.

3 路径寻优TSP的一般求解

TSP是一个世界性的难题，人们曾提出了许许多多近似的解法试图找到一个次优的近似解。这些算法虽然求出的是近似最优解，却大大降低了计算量。传统求解中，曾用优化方法主要有以下几种。

1）长度优化法 优先考虑刀具移动路径的长度，使其最小化。如图1中的（a）所示；

2）刀具优化法 优先考虑刀具的换刀次数，使其最小化。如图1中的（b）所示；

3）混合优化法 综合考虑路径长度与换刀次数，使加工时间最短。如图1中的（c）所示。

图1 长度优化法、刀具优化法和混合优化法Fig.1 The length optimization，the tool optimization and the hybrid optimization

4）X或Y单向优化法 将待加工孔按照中心的X或Y坐标排序，此方法较适合冲孔中存在直线均布或阵列分布，其排序按照仅沿着X向或Y向进行刀具路径的规划，则又可分为X向路径法和Y向路径法2种。X向路径法：将所有待加工孔中心按照其坐标值进行排序，排序原则是按X值从小到大的顺序，当X值相等时，按Y值排序，Y值的排序原则取决于上一点的Y值，当上一点的Y值大于等于当前点的Y值时，则按照从大到小的顺序，否则按从小到大的顺序。Y向路径法：同样也是将所有待加工孔的中心按照其坐标值进行排序，只是排序原则中首先按Y值排序，Y值相同时再按X值排序，其余的思想完全相同。X向冲孔路径优化实例如图2所示，Y向冲孔路径优化实例如图3所示。由于数控冲床本身的原因，机床结构的几何误差导致在加工点处产生三维位置误差，对加工工件精度影响很大。数控机床轴线的反向间隙会影响坐标轴的定位精度，而定位精度的高低在孔群加工时，不但影响各孔之间中心距，还会由于定位精度不高，造成加工余量不均匀，引起几何误差。如果在加工过程中，刀具不断地改变趋进方向，就会把坐标轴反向间隙带入加工中，造成定位误差增加，为提高加工精度，要求刀具的移动是单向的，应尽可能单向趋进目标点进行加工，避免空回程误差的引入。

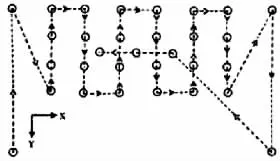
图2 X向冲孔路径优化法Fig.2 X-direction optimization

图3 Y向冲孔路径优化法Fig.3 Y-direction optimization

5）邻近优化法 当待加工孔的位置在二维平面内任意排布时，为了简便易行，采用最近点路径法，其基本步骤如下：以待加工孔中任一孔位为原点，先走到与其最邻近的1点，然后继续在没有走过的点中选最邻近点，直至将所有点都选过为止。 例如某零件上有 n个待加工孔 P1，P2，…，Pn，首先以 Pl作为起始点，在剩余的n－1个点中寻找距离Pl最近的点作为第2点，再在剩余的n－2个点中寻找距离P2最近的点作为第3点，依此类推直至将所有的点排序完为止，得到一条刀轨路径；然后再分别以 P2，P3，...，Pn为起始点进行排序，得到另外n－1条路径。该方法在应用于待加工孔分布密度比较均匀的情况下，能够获得比较理想的解。但当待加工孔分布不均匀时，会出现刀具的跨越现象，增加空行程。邻近优化法实例如图4所示。

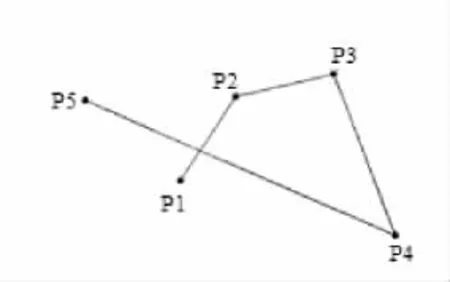
图4 邻近优化法Fig.4 Nearest neighbor optimization

最近邻居点算法容易理解，编程简单，可靠性较高，是目前解TSP问题中最广泛采用的方法。但这一方法的近似精度在组合数学中已被证明为n≤1/2（1n N+1），它在算法计算复杂性为。从近似精度看，这种方法有时也可能很差，远达不到次优，应用于多孔加工时具有较高的计算复杂性。

6）亲近点优化法 采用邻近算法时，由于最后一点没有与任何点进行比较，故而需对最后一点进行测试。例如有n个点 Pl，P2...，Pn，以 Pl作为起始点得到最近邻居路径后，比较Pn－1Pn（表示点 Pn－1到点 Pn距离， 方向为点 Pn－1指向点 Pn）与P1Pn，如果 Pn－1Pn远大于 PlPn，则修改最近邻居的路径，将 Pn分别与 P1和 P2相连，即得到 PlPn与 PnPn－1，从而产生亲近点优化路径，当出现多个跳跃点时，亲近点优化法将失效。

7）蚁群算法 是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法。蚁群在觅食时即使环境不断改变，总能找出一条从食物到巢穴的最优路径。这是因为蚂蚁在寻找路径时会在路径上释放一种特殊的信息素，当他们遇到一个还没有走过的路口时，就随机地挑选一条路径前行，同时释放与路径长度有关的信息素，路径越长，释放的信息素浓度越低。当后来的蚂蚁再次遇到这个路口时选择信息素浓度较高的路径概率就会相对较大，这样大量蚂蚁组成的蚁群集体行为便形成了一种信息正反馈现象，最优路径上的激素浓度越来越大，而其它路径上的信息素浓度却会随时间的流逝而消减，最终整个蚁群会找到最优路径。

在以上算法中长度优化法、刀具优化法、混合优化法、最近邻居点优化法、亲近点优化法对冲压特征较少的情况下比较适用，当特征较多时容易陷入局部最优解。

4 路径寻优TSP的GA求解

当前经典遗传算法及各种改进的遗传算法作为解决TSP的一类有效方法，已经得到不少应用。它具有全局搜索能力和广泛的适用性等优点，解决的问题无论是否凸性的，理论上都能获得最优解，避免落入局部极小点。因此，该文采用改进的遗传算法寻找最优换刀路径，将选择、交叉、变异等概念引入到算法中，通过对包含可能解的种群反复使用基于遗传学的操作，这个过程将导致种群像自然进化一样，其后代种群比前代更加适应于环境，种群中的最优个体经过解码，可以作为问题近似最优解。

4.1 GA在路径寻优中的优势

GA就其本质来说，主要是处理复杂问题的一种鲁棒性强的启发式随机搜索算法，与传统优化方法相比，具有如下的优点：1）遗传算法的搜索过程不是直接作用在问题的变量上，而是作用在将变量编码后的字符串上，即遗传算法是一种间接的优化方法而非直接的优化方法；2）遗传算法的搜索过程不是从一个点到另一个点，而是从一个群体到另一个群体，不易陷入局部最优解；3）遗传算法使用概率规则而非确定性规则指导搜索方向，属于随机性优化方法而非确定性优化方法；4）遗传算法属于非数值计算优化方法，对所求解的问题的数学模型无特殊要求，既不要求问题的可行域是连通的、凸的，也不要求问题的目标函数可微，只要求问题是可计算的；5）遗传算法的搜索过程只依赖于个体的适应度函数，不需要其它的辅助信息，具有很好的鲁棒性和广泛的适应性；6）遗传算法虽然每次处理的个体数量有限，但每次处理的数量远多于个体数量，即遗传算法具有隐含并行性。

4.2 GA路径寻优工作流程

钢构打字过程中，需要对刀塔加工用的加工代码文件进行分析，将每次换刀后的路径段作为一个路径组，加工过程如下：从某一个给定的字符开始，换上对应的刀具后，沿着该刀具总的空行程最短的轨迹，从一个字符点位移动到另一点位，直到所有该字符都被加工完毕，再进行下一字符的加工，如此循环。在这里，刀具实际上充当了旅行商的角色，字符点位充当了城市的角色，目标为加工过程中刀具的空行程最短。该研究正是把打字点位看做TSP问题，利用遗传算法特殊搜索方式，对工业钢构打字的刀具移动轨迹进行寻优求解，得到了满意的结果。图5所示为遗传算法的工作流程图，表示一个迭代的过程，其需要完成的工作内容和步骤如下：1）选择编码策略，随机产生初始种群P；2）定义适应度函数f（x），计算各染色体的适应度值，以适应度值对染色体进行评价；3）选择高适应度值的染色体进入下一代；4）按照遗传策略，运用选择、交叉和变异算子作用于群体，产生下一代群体；5）按照终止准则判断群体性能是否满足某一指标，或者已完成预定迭代次数，不满足则重复2）～4）步，直到满足性能要求或达到预定的进化次数。

5 应用GA求解TSP的实例仿真

图5 遗传算法的工作流程Fig.5 Flow chart of GA

Matlab系列软件是工程数学计算特别是线性数学计算的得力工具，为检验该研究的正确性及实用性，这里选择使用Matlab7.0作为算法的运行环境，用 Matlab工具箱对遗传算法求解钢构打字过程中TSP问题的效果进行验证。图6所示即为某钢板打字过程中，对其中某一字符进行路径寻优的效果图。经仿真实验测得，未加改进GA优化后的路径长度为1 933.955 413 mm，用该研究选取的改进型GA优化后的路径长度1 803.558 802 mm，路径缩短6.742 482%，优化效果明显。

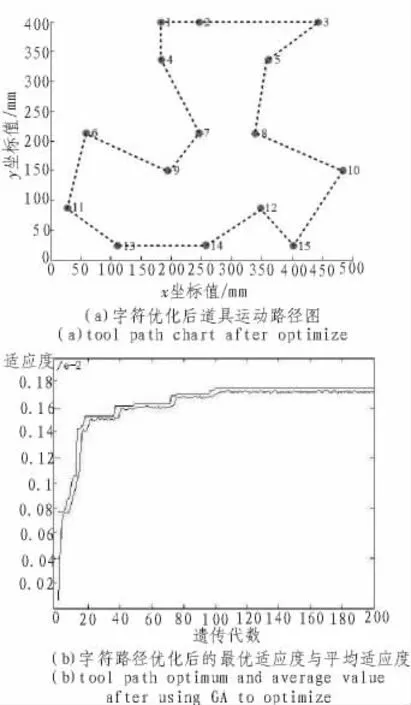
图6 路径寻优效果图Fig.6 Path optimization rendering

6 结 论

研究基于TSP的数学模型和字符点群加工路径优化模型，结合转塔打字实例，以刀具的非加工行进成本最低为目标建立了字符点群单目标路径优化模型，采用Matlab遗传算法程序进行了优化求解，最终找到了最短路径，实现了路径优化。而对于空间字符点群的加工，既要保证刀具行进路径最短，又要保证设备的空间变向次数最少，这样才会最大限度地减少刀具的行进时间、变向时间，从而大大地降低成本。

[1]边霞，米良.遗传算法理论及其应用研究进展[J].计算机应用研究，2010，27（7）:2425-2429.BIAN Xia，MILiang.Development on genetic algorithm theory and its applications[J].Application Research of Computers，2010，27（7）:2425-2429.

[2]谭跃，谭冠政，叶勇，等.具有混沌局部搜索策略的双种群遗传算法[J].计算机应用研究，2011，28（2）:468-470.TAN Yue，TAN Guan-zheng，YE Yong， et al.Dual population genetic algorithm with chaotic local search strategy[J].Application Research of Computers，2011，28（2）:468-470.

[3]张艳琼.改进的云自适应粒子群优化算法[J].计算机应用研究，2010，27（9）:3250-3252.ZHANGYan-qiong.Improved adaptive particle swarmoptimization algorithmbased on cloud theory[J].Application Research of Computers，2010，27（9）:3250-3252.

[4]吕明明，王平江.高速转塔冲床专用数控系统的研究及开发[J].组合机床与自动化加工技术，2011（5）:51-54.LV Ming-ming，WANG Ping-jiang.The research and development of the numerialcontrol system for high-speed turretpunch press[J].Modularm Achine Tool&Automaticm Anufacturing Technique，2011（5）:51-54.

[5]罗宏保，董红召.车削中心转塔刀架布刀的GA优化方法[J].农业机械学报，2007，2（38）:172-175.LUO Hong-bao，DONG H ong-zhao.GA-based approach to optimize cutters arrangement on the turret post of turning center[J].Agricultural Machinery，2007，2（38）:172-175.

[6]朱林杰.基于TSP的遗传算法优化研究[D].大连：大连理工大学，2007.

[7]侯建花.TSP遗传算法的改进及其并行化研究[D].成都：成都理工大学，2004.

[8]张雁，黄永宣，魏明海.一种求解最大团问题的自适应过滤局部搜索算法[J].信息与控制，2011，40（4）:445-451.ZHANGYan，HUANGYong-xuan，WEIMing-hai.An adaptive filtered local search algorithmfor the maximumclique problem[J].Information and Control，2011，40（4）:445-451.