水下爆炸作用下舰船总纵强度模型实验方案研究

张海鹏，岳永威，苏罗青，张阿漫，姚熊亮

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

提高舰船的抗爆抗冲击性能和生命力是保证舰船发挥其作战能力［1］的一项重要前提，各国海军十分重视该方面的研究。对舰船进行实船爆炸实验是评估舰船总纵强度最准确有效的方式，但需要耗费大量的资金，且实施较为困难。因此，许多发展中国家在评估舰船水下爆炸作用下的总纵强度［2-3］方面，基本上采用舰船缩比模型开展水下爆炸实验来评估，此时会产生这样的矛盾:若缩尺比较大，则实验费用居高不下，开展缩比模型实验的意义大为降低;若缩尺比较小，缩比模型的尺寸会非常小，模型在制造工艺上存在较大困难，且换算到实船上结果的准确性也得不到保证，我国虽然开展了一些缩比模型的水下爆炸实验，但其缩尺比均较小，模型与实船既未能达到完全几何相似，也不存在畸变相似关系，因此其实验结果难以评估与考核实船的抗爆抗冲能力。

在评估舰船总纵强度水下爆炸实验中，若采用合适的缩尺比，再以此舰船缩比模型为基准模型，根据弹性结构畸变准则，选择合适的畸变参数对基准模型中几何尺寸较小的板梁进行畸变，使用畸变模型进行实验。这样，不仅能解决模型在制造工艺中的困难，还可以在降低实验成本的前提下实现准确预测舰船原型总纵强度的目的。本文的加载方式考虑了水下爆炸冲击波和气泡载荷的一次相似律，并利用弹性结构畸变准则对基准模型进行畸变，通过数值计算手段得到满足工程精度、制造工艺、经济性等要求的舰船总纵强度模型实验方案。

1 缩比模型水下爆炸相似规律

多年来，国内外许多学者一直致力于水下爆炸“相似律”的研究和探索，寻求通过缩比模型实验预测原型结构动响应特性的方法，现今也取得了许多具有学术价值［4］的成果。水下爆炸是一个很复杂的物理过程，分为冲击波和气泡脉动两个阶段，流体的特性也会在不同的阶段发生变化，如果简单的将模型加载方式用同一个冲击波、气泡脉动相似准则处理，得到的模型实验数据结论将与原型发生偏差，甚至背离。因此需要对水下爆炸产生的冲击波和气泡的相似律分别讨论。另外在工程实际中，某些时候缩比模型的相似条件不能满足，如模型中的板或梁的几何尺寸按缩尺比进行缩尺，缩比后的模型在制作中会产生诸多问题，如焊接难度大、所需规格市场上不存在，因此就必须利用弹性结构的完全相似理论及畸变准则对基准模型的结构进行改造得到畸变模型，最终实现对原型总纵强度的准确预测。

1.1 冲击波载荷相似律

自由场中水下爆炸冲击波现象区别于一般水动力学现象，它的作用力是瞬态的并且具有很强的冲量，水动力学中一些相似常数(如Fr数)可以不必讨论。本文仅考虑自由场中的水下爆炸问题，要使自由场水下爆炸中冲击波阶段的过程相似，必须使各基本相似量间满足一定的相似条件，即:

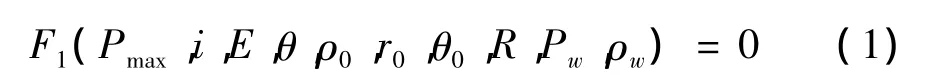
若用装药量W表示，即r0=，相似条件可利用经验公式［7］由已知的方程导出:

同理可求得:λE=λi=λθ=λl，即当模型的几何尺寸、加载形式与原型相似时，两者的压力峰值是相同的，而脉冲持续时间、冲量、比冲量、能量密度将按特征长度相似常数(λl)换算。

1.2 气泡脉动载荷相似律

对于自由场中水下爆炸气泡脉动问题，本文假定气泡膨胀时周围的水产生径向运动，而没有垂向位移，即不考虑与气泡上浮时流体静压变化有关的流体静浮力的影响［8］。在这个假定的条件下，要使自由场水下爆炸中气泡脉动阶段的过程相似，必须使各基本相似量间满足一定的相似条件，即:

式中:Pd为爆深D(m)处静水压(Pa)，等于D+D0(m)水柱压强，D0为大气压的水柱压强;为气泡脉动压力峰值;T为一次气泡脉动周期;θ为衰减系数;ρ0为装药密度;r0为装药半径;Ep为单位质量气泡能;为气泡最大半径;ρw为水密度。选定Pd、ρw和r0为基本物理量，同样由π定理得到各物理量函数关系式为:

以一次气泡脉动周期项T项作为因变项，并用装药质量及水柱表示，经转换得到Ep、和各物理量与周期的函数关系式分别用G3、G4和G5表示［6］:

由经验公式［6］:

类比后求得关系式［6］:

综上所述，在不考虑重力效应影响的情况下，自由场中气泡脉动相似的的充分必要条件是:(D+D0)是个常量。要实现这一充要条件，必须使用将实验水池做封闭增压处理，在(D+D0)一定时，当模型的几何尺寸、加载形式与原型相似时，在一次气泡脉动阶段，气泡最大半径、脉动周期以及脉动频率按特征长度相似常数(λl)换算，气泡脉动峰值不变。事实上，以目前国内的实验条件，通过对水池进行封闭增压来实现水下爆炸一次气泡脉动的相似难以实现，大部分模型试验主要在露天水池中进行，此时(D+D0)就不可能是一个常量，对气泡脉动的模拟就存在误差，然而，要得到在不考虑对实验水池进行封闭增压处理时，大缩尺比船模水下爆炸实验进行原型总纵强度预报的误差范围，还需要严格的理论推导及大量实验，本文主要介绍水下爆炸实验模型的选取方法，这里不做详细讨论。

1.3 舰船模型畸变相似准则

船体板格通常为矩形板，按边界不同大致可分为刚性固定、弹性固定、弹性支持和简支。下面以均布荷重P(t)作用下四边刚性固定的矩形板为例，讨论其板厚不能按特征长度相似常数λ缩小时的畸变修正方法。此时将均布荷重P(t)作用下四边刚性固定的矩形板作为一个系统，取表征系统这一现象的物理量:均布荷重P(t)、时间t、板厚d，t时刻的位移U(t)、t时刻的应变ε(t)、t时刻的应力σ(t)、材料泊松比μ、结构固有频率f、系统总能量Q、材料密度ρ、t时刻的结构尺寸L(t)和弹性模量E，共12个物理量。当缩比模型与原型使用同种材料时有:

当板厚不能按特征长度相似常数λL(t)缩小时，定义完全几何相似模型为基准模型(上标“m”代表基准模型的∏项和物理量)，以基准模型为基础仅对板厚进行畸变的模型定义为畸变模型(上标“b”代表畸变模型的∏项和物理量)。对于基准模型和畸变模型，仅有相似常数λd≠λL(t)，其它各相似常数均为1时，缩比模型发生畸变，定义“板厚畸变系数”为 φ，根据文献［9-11］有:

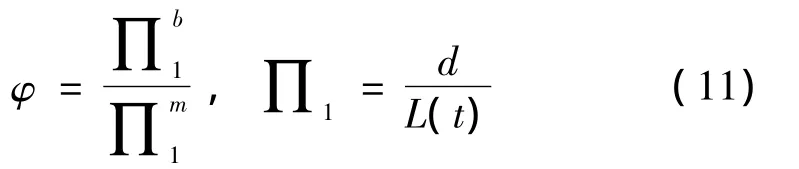
设畸变模型和基准模型时间的因变∏项的比值为δt，称之为“时间预测系数”。即:

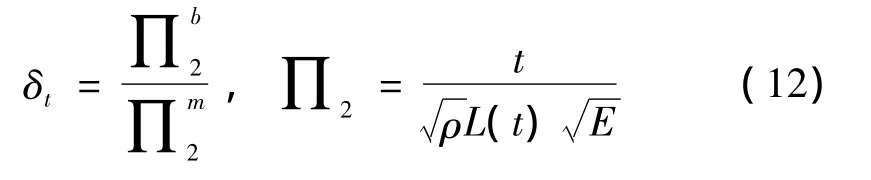
时间预测系数δt仅是畸变系数φ的函数，通过大量实验测量或数值计算的方法可得到δt随φ变化的规律，进而确定其函数形式和最终结构畸变准则。相关文献表明［11］，弹性体结构基于该方法确定的畸变准则进行畸变，得到的模型计算结果与基准模型有很高的一致性，并且在制作工艺上的可控性好。

2 计算结果分析

为选定舰船总纵强度模型实验的最优方案，本文对四种舰船缩尺实验方案进行水下爆炸数值计算分析，并对实际模型横剖面弯矩预测偏差进行总结，得到既能使实验模型在工程精度范围内实现对原型横剖面弯矩的准确预测，同时又满足制造工艺的可控性和实验成本的经济性的最终实验方案。

2.1 模型实验计算工况设定

本文以XXX舰有限元模型为原型，如图1所示，选取攻击武器为MDM-X型水雷，爆心位于船舯正下方，见图2，装药质量相当于m=Wkg的TNT，调整爆距R=Z0m，使其气泡周期［7］与船体湿模态一阶固有频率相同，使气泡脉动载荷激起船体共振，探究XXX舰此典型工况下的总纵强度。

为了评估缩比模型与原模型的数值计算结果，本文选取了延船长方向上三处典型剖面部位进行横剖面弯矩时历曲线输出，分别为船舯横剖面、X1横剖面、X2横剖面，具体示意图如图3，其中X1=X2。

2.2 完全几何相似模型实验方案

为了选择合适的缩尺比，本研究提出四种完全几何缩比模型实验方案与原型进行对比分析，采用自由场中水下爆炸一次冲击波和气泡脉动相似理论对模型进行相似加载，并考虑实验模型的经济性及可操作性等因素，确定合适的缩比模型，为下一步畸变模型实验方案做准备。对上述舰船完全几何缩小，舰船、药包原型与缩比模型相似关系见表1，其中Dp为爆深D(m)处的水柱压强，(D0)p=10.33 m为大气压的水柱压强。

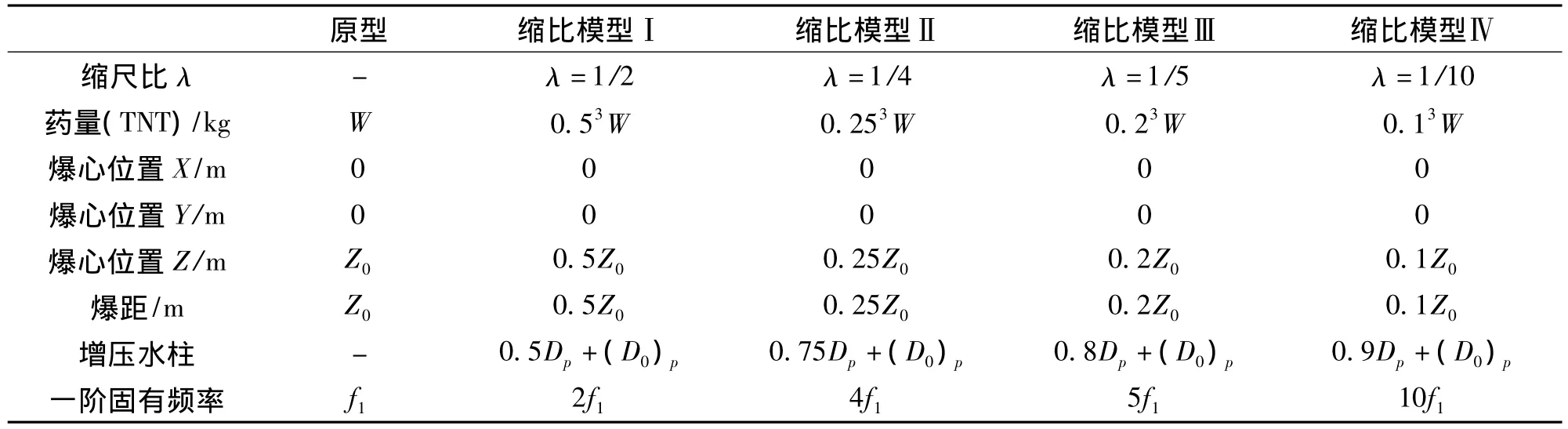
表1 XXX型舰原型与模型相似关系Tab.1 Similarity relation between the model and the archetype of XXX ship

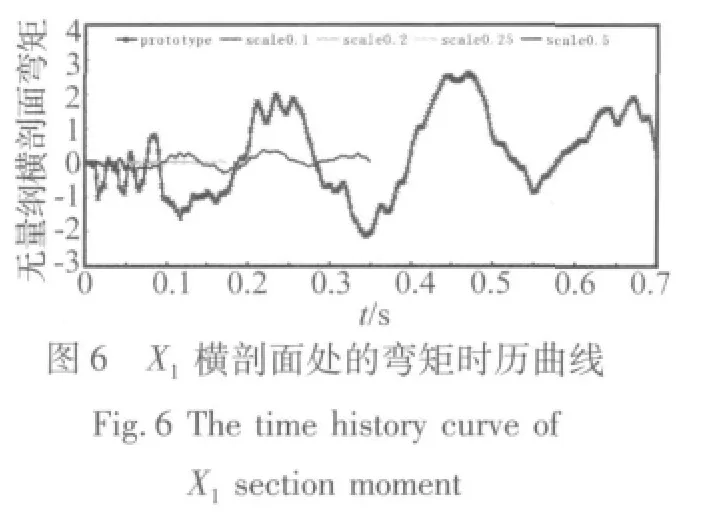
下面分别给出XXX舰及其缩比模型在静水中遭受水下爆炸载荷作用时各个考核剖面的无量纲横剖面弯矩时历曲线。此处的原型与缩比模型弯矩时历曲线由相应剖面的输出点拟合而得，将各模型时历曲线的输出点横坐标t按时间缩尺比放大，同时将各输出点纵坐标M按相应的弯矩缩尺比放大，即得到相似处理后的模拟时历曲线。无量纲横剖面弯矩时历曲线的原型与缩比模型相比，缩比模型的横剖面弯矩缩尺比按特征长度相似常数三次方即换算，缩比模型的时间缩尺比按特征长度相似常数λl换算，相似处理后的时历曲线结果如图4～图9(数据已经过无量纲处理):

从上图可以看出，应用自由场中水下爆炸一次冲击波和气泡脉动相似理论处理后的缩比模型与原型的典型考核横剖面弯矩时历曲线基本吻合。应用完全几何相似模型，可以通过模型实验非常准确地预测原型结构遭受水下爆炸载荷时的结构响应特性及其总纵强度。

2.3 畸变模型实验方案

完全几何相似模型中的板或梁的几何尺寸(如厚度)按缩尺比进行缩尺时，会出现如焊接难度大、钢材规格难以实现等问题，必须使用畸变模型。模型畸变后，图3所考虑的考核剖面抗弯刚度必定发生变化，保证畸变模型预测精度的关键在于合理选取畸变系数φ，由前文推导可知，预测系数δt是畸变系数φ的函数，但二者的函数形式并不确定，而且不同模型的畸变系数函数形式也不尽相同，实际上，预测系数δi与φ的函数关系可以通过一系列模型试验来确定，但这样做需要耗费大量的人力物力，显然工程上是不可取的。因此，本文采用有限元预测系数法寻找预测系数δi随畸变系数φ的变化规律。具体方案如下:首先定义完全几何相似模型为基准模型，以基准模型为基础，仅对板厚进行畸变的模型定义为畸变模型，建立系列畸变模型和基准模型之间的预测系数δi=F(φ)函数关系，结合完全几何相似理论，实现对原型动响应特性的预报。

数值实验结果表明，当畸变系数φ=3(板厚为3h的模型Model 4)时，畸变模型对原型的预测误差最小。下面分别给出当畸变系数φ=3时，XXX舰的基准模型及各畸变模型的在静水中遭受水下爆炸载荷作用无量纲横剖面弯矩时历曲线，及经过相似处理的无量纲横剖面弯矩时历曲线对比图。

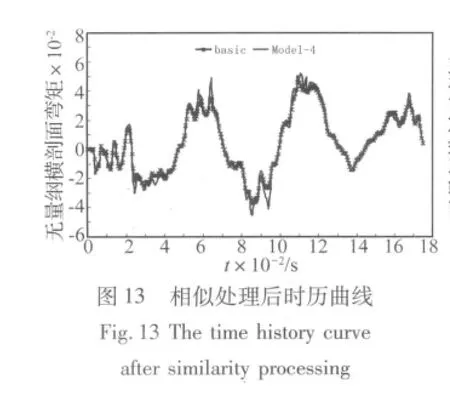
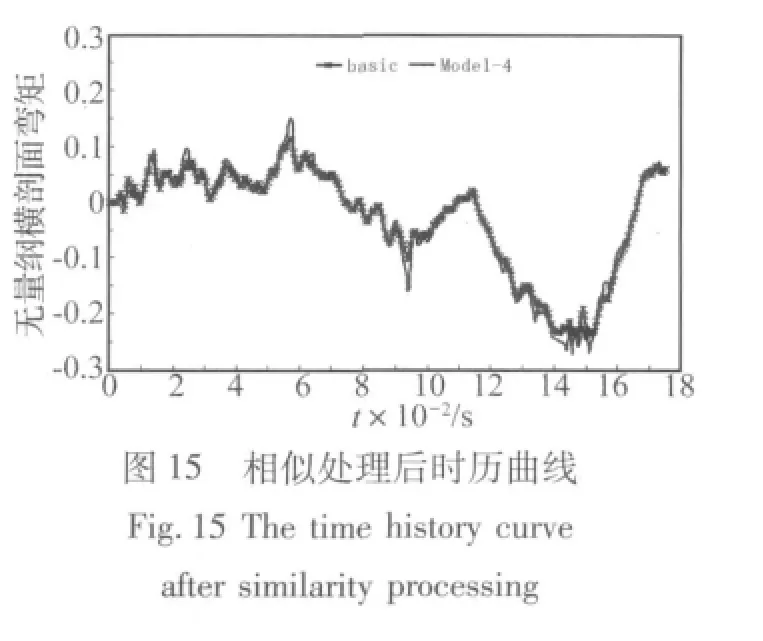
选取以上横剖面的动响应峰值进行预测偏差分析，见表2:

表2 典型部位弯矩峰值预测偏差分析Tab.2 Deviation analysis of moment peak of typical position

表3 畸变实验模型评估表Tab.3 Evaluation table of distortion experimental model

3 结论

本文基于自由场中水下爆炸一次冲击波和气泡脉动相似律，通过数值实验手段研究了在大缩尺比船模水下爆炸实验中，使用畸变模型实现对原型总纵强度准确预测的方法。通过对实验结果的分析可得到的结论及建议如下:

(2)应用完全几何相似模型，可以通过模型实验准确地预测原型结构遭受水下爆炸气泡脉动载荷时的结构响应特性及其总纵强度。

［1］汪 玉.舰船现代冲击理论及应用［M］.北京:科学出版社，2005:21-29.

［2］徐培誉.水下爆震对结构之响应［D］.台北:国立台湾大学，2004.

［3］ Keil K A.The response of ship to underwater explosion［J］.SNAME，1961，69(4):366-410.

［4］程素秋，宁永成，张 臣，等.相似理论在水下爆炸模型实验中的应用［J］.船舶科学技术，2008，30(3):96-99.

［5］张 亮，李云波.流体力学［M］.哈尔滨:哈尔滨工程大学出版社，2007:179-187.

［6］张效慈.水下爆炸实验相似准则［J］.船舶力学，2007，2(1):108-118.

［7］库尔P，罗耀杰，等译.水下爆炸［M］.北京:国防工业出版社，1960.

［8］Klaseboer E，Khoo B C，Hung K C.Dynamics of an oscillating bubble near a floating structure［J］.Journal of Fluid and Structure，2005，21:395-412.

［9］ Gel’fand B E，et al.Similarity criteria for underwater explosion［J］.Combustion，Explosion，and Shock Waves，2004，40(2):214-218.

［10］徐 挺，著.相似方法及其应用［M］.北京:机械工程出版社，1995.

［11］谢建林.瞬态载荷作用下弹塑性结构动响应相似性研究［D］.哈尔滨:哈尔滨工程大学，2008:24-55.