一种基于样本熵的轴承故障诊断方法

赵志宏，杨绍普

(1.北京交通大学 机械与电子控制工程学院，北京 100044;2.石家庄铁道大学 信息科学与技术学院，石家庄 050043)

滚动轴承是机械设备中最常用且最容易损坏的零件之一，当发生故障时损失巨大，因此轴承故障诊断技术得到人们的重视［1-3］。特征提取是轴承故障诊断中非常关键的一个环节，提取的特征如能正确地反映故障类别，则为模式识别打下基础。

当轴承存在故障时，表现出非线性、非平稳特征。传统的基于线性系统的特征提取方法不能有效提取故障的非线性特征。基于非线性动力学参数的特征提取方法提供了一种研究机械故障非线性特征的工具，近年来这种方法引起了人们广泛的关注。至今，已有许多非线性参数识别方法用在机械故障诊断领域，其中，使用较多的有关联维数方法［4-5］。Yan［6］引入近似熵(Appropriate Entropy，ApEn)概念并将其用于轴承状态监 测。Pincus［7］提 出 的 样 本 熵 (Sample Entropy，SampEn)是近似熵的改进算法，它的优越性在于可以较少地依赖于时间序列长度，已经广泛地用于生理信号处理［8-9］。

Huang等人［10］提出的经验模式分解方法(Empirical Mode Decomposition，EMD)可以根据振动信号自身的时间特征尺度进行自适应分解，将轴承振动信号的状态信息分解到不同的内蕴模式分量(Intrinsic Mode Function，IMF)中，从而为轴承状态深层次的挖掘奠定了基础。EMD方法的一个主要问题是模式混淆问题，使得各IMF分量不能反映信号的真实内涵。集成经验模式分解方法(Ensemble Empirical Mode Decomposition，EEMD)［11］是对 EMD 的改进，可以有效解决模式混淆问题。因此，针对利用原始轴承振动信号的样本熵无法准确反映轴承故障信号的特征问题，采用先对原始信号进行EEMD分解，再对获得的内蕴模式分量进行SampEn分析，这样可以获得轴承状态信号更深层次的信息。

本文在对轴承振动信号的样本熵深入分析的基础上，提出一种基于EEMD分解，利用样本熵作为特征的轴承故障诊断方法，并通过轴承正常状况、内圈故障、滚动体故障、外圈故障实测振动信号进行验证，实验结果表明了该方法的有效性。

1 样本熵介绍

一般地，对于由N个数据组成的时间序列{x(n)}=x(1)，x(2)，…，x(N)，样本熵的计算方法如下［12］:

(1)按序号组成一组维数为m的向量序列，Xm(1)，…，Xm(N-m+1)，其中Xm(i)={x(i)，x(i+1)，…，x(i+m-1)}，1≤i≤N-m+1。这些向量代表从第i点开始的m个连续的x的值。

(2)定义向量Xm(i)与Xm(j)之间的距离d［Xm(i)，Xm(j)］为两者对应元素中最大差值的绝对值。即:

(3)对于给定的Xm(i)，统计Xm(i)与Xm(j)之间距离小于等于r的j(1≤j≤N-m，j≠i)的数目，并记作Bi。对于1≤i≤N-m，定义:

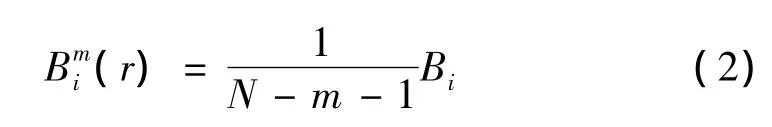
(4)定义B(m)(r)为:

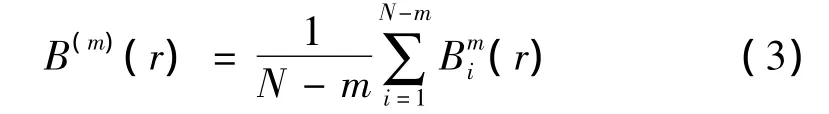
(5)增加维数到m+1，计算Xm+1(i)与Xm+1(j)(1≤j≤N-m，j≠i)距离小于等于r的个数，记为Ai。(r)定义为:

(6)定义Am(r)为:

这样，Bm(r)是两个序列在相似容限r下匹配m个点的概率，而Am(r)是两个序列匹配m+1个点的概率。样本熵定义为:

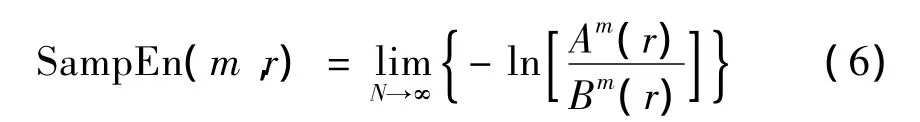
当N为有限值时，可以用下式估计:

可以看到，样本熵的值与m，r的取值有关。因此，确定m，r两个参数的值对于样本熵的计算非常重要。这里，根据 Pincus［9］的研究结果，m=1 或 2，r=0.1 Std～0.25 Std(Std 是原始数据x(i)，i=1，2，…，N的标准差)计算得到的样本熵具有较为合理的统计特性。在本文的研究中，取m=2，r=0.2 Std。

2 利用样本熵分析轴承信号

图1 实验装置Fig.1 The test rig

实验所用的实测轴承振动加速度数据来自于Case Western Reserve University(CWRU)［13］。实 验装置如图1所示，滚动轴承的型号为SKF6205，轴承状态包括正常、内圈故障、滚动体故障和外圈故障四种类型，轴承的损伤状况为单一损伤，是由电火花机分别在轴承内圈、滚动体和外圈人工加工制作，损伤的直径分别为0.177 8 mm，0.355 6 mm，0.533 4 mm和0.711 2 mm。电机的负载由风机来调节，产生的载荷为0～2 206.496 W。将振动加速度传感器垂直固定在感应电机输出轴支撑轴承上方的壳上进行数据采集，采样速率为12 k。

2.1 数据长度对样本熵的影响

图2显示了当损伤程度为0.177 8 mm，载荷为0，转速为1 797 r/min，取样速率为12 k时，样本熵的值与数据长度取值的关系。从图中可以看到，当数据长度小于500时，不同数据长度，样本熵的值有很大变化;而当数据长度大于500时，样本熵的值比较稳定。另外，轴承在不同故障下，样本熵的值也不同;轴承在正常情况下，样本熵的值比较小，当故障出现时，样本熵的值变大。从图2中可以看出，样本熵可以很好地表明轴承的运行状况。

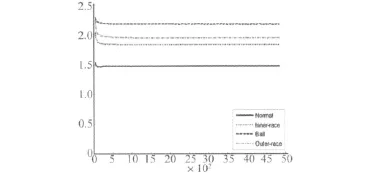
图2 数据长度对样本熵的影响Fig.2 The influence of data length on the SampEn

一些典型数据长度取值的样本熵均值与标准差如表1所示。从表1可以看出，轴承在四种情况下，取不同数据长度时标准差的值都比较小，说明了对于不同的数据样本，样本熵计算结果的变化不大;而不同故障情况下样本熵的取值有很大不同，表明样本熵可以很好地作为轴承故障诊断的特征。另外还可以看到，随着数据长度变大，标准差的值变小(虽然变化不是大)，说明数据长度越大，样本熵的值越稳定。因此，数据长度取值越大越好，但是，由样本熵计算方法可以知道，数据长度越大，计算时间也越长，综合考虑之后，选取数据长度为2 048。本文后面部分样本熵计算的数据长度都取此值。

2.2 损伤程度对样本熵的影响

取载荷为0，转速为1 797 r/min，损伤程度依次为0.177 8 mm，0.355 6 mm，0.533 4 mm，0.711 2 mm 的数据进行实验。轴承在不同故障、不同损伤程度下样本熵的值如表2所示。从表2可以看到，在三种故障情况下，随着损伤程度改变，样本熵的取值也不同，但并不是损伤程度越大，样本熵值越大。而是在轻微损伤(0.177 8 mm)的情况下，样本熵的取值比较大，然后，随着损伤程度的加大，样本熵的值先变小，当到一定程度后，样本熵的值又变大。说明样本熵对轻微损伤比较敏感。不同故障情况下，样本熵值的变化规律不同。但是在同样损伤程度情况下，内圈故障、滚动体故障、外圈故障的样本熵值不同。

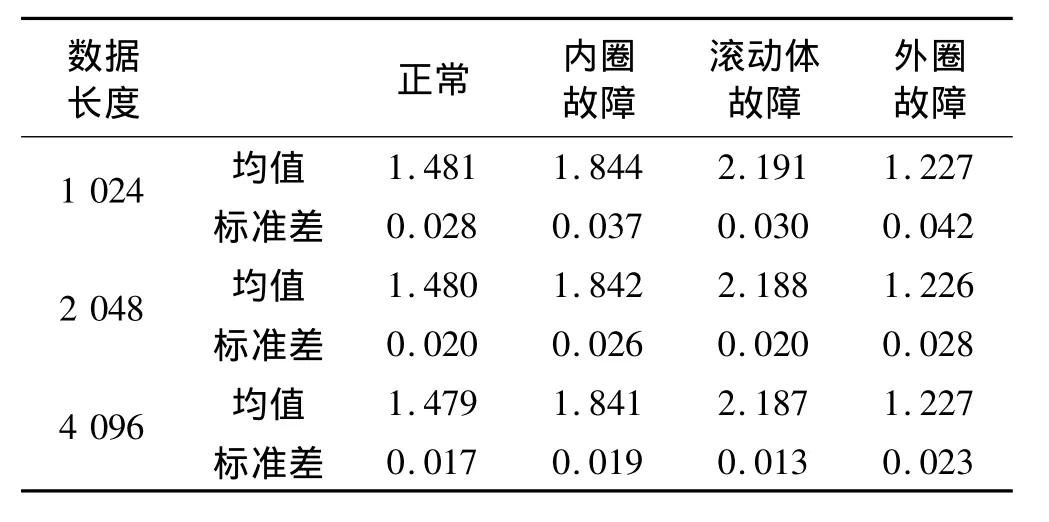
表1 不同数据长度轴承样本熵的均值与标准差Tab.1 The average and standard deviation SampEn of different data length

表2 损伤程度对样本熵的影响Tab.2 The influence of fault diameter on the SampEn

2.3 载荷对样本熵的影响

取损伤程度为 0.177 8 mm，载荷分别为 0、735.49875W、1470.998W、2206.496W 马力，对应转速分别为 1 797 r/min，1 772 r/min，1 750 r/min，1 730 r/min的测试数据。轴承在不同载荷下样本熵的取值如表3所示。从表中可以看到，载荷对样本熵的取值有影响。在正常情况下，载荷越大，样本熵取值越大。载荷对滚动体故障的影响较小。当轴承出现内圈故障与外圈故障时，并不是载荷越大，样本熵值越大。在同样载荷作用下，轴承在正常情况、内圈故障、滚动体故障、外圈故障情况下样本熵的取值明显不同。可以从表3得知，当出现损伤情况下，轴承振动信号的样本熵值会变大。

表3 载荷对样本熵的影响Tab.3 The influence of motor load on the SampEn

3 集成经验模式分解

Huang等人［10］提出的经验模式分解方法(EMD)目的是将待分析信号分解为一系列表征时间尺度的IMF分量，使得各IMF分量是窄带信号，满足Hilbert变换的要求，即IMF分量必须满足两个条件:采样数据的极大点和极小点数之和与过零点的个数之差不超过1;在任意点，由局部极大值和局部极小值定义的包络均值必须为零。

EMD的分解过程其实是一个“筛分”过程，在“筛分”的过程中，不仅消除了模式波形的叠加，而且使波形轮廓更加对称。EMD算法的实现过程可参考文献［10，14］。

经验模式分解基本方法的缺点是存在模式混淆问题，模式混淆掩盖了各IMF分量蕴含的信号真实内涵，导致对象的物理本质不清晰。集成经验模式分解［11］(EEMD)通过叠加高斯白噪声，使分解得到的IMF分量更真实，更能反映信号的本质过程。EEMD算法描述如下［11］:

(1)向待分解的原始数据中加入一个随机高斯白噪声序列;

(2)对含有白噪声的数据进行EMD分解，得到其内蕴模式分量IMFs。

(3)重复执行步骤(1)～(2)，但是每次增加不同的白噪声序列。

(4)将多次EMD分解得到的对应的内蕴模式分量进行平均，作为最终的IMF分量。

EEMD通过在原始数据上叠加随机白噪声序列，从而改变一次EMD分解中的特征尺度，通过多次EMD分解，相当于从多个特征尺度提取原始数据的本质，最后利用各内蕴模式分量IMF的均值作为最终的IMF，因此，与单次EMD分解相比，可以更准确地揭示数据的真实物理意义。研究证实，EEMD可以有效抑制EMD中的模式混淆问题。基于以上考虑，本文选择EEMD进行轴承振动信号的分解。

轴承正常信号与外圈故障信号的EEMD分解结果如图3所示，图中只列出了前8个IMF分量，从图3中可以看到，各个IMF分量包含了不同的时间特征尺度，使得轴承故障特征在不同的时间尺度下显露出来，第1个IMF分量的频率成分最高，第2～7个IMF分量的频率成分依次降低。轴承故障信息在高频段，因此，使用前4个IMF分量的样本熵作为轴承故障诊断的特征。另外，从图3中可以看到，正常轴承振动信号和外圈故障轴承振动信号得到的IMF分量明显不同，外圈故障信号的imf1，imf2分量可以明显看出存在周期性冲击信号特征，imf3，imf4分量可以看到存在冲击信号特征，但周期性并不明显。而正常轴承振动信号得到的imf1分量可以看到一些与转速等有关的周期特征，并且该周期大于外圈故障信号imf1分量的周期，这与轴承外圈故障振动信号的特征频率较高一致。从图3中可以看到，轴承故障振动信号的EEMD分解得到的IMF分量中包含了轴承的故障特征信息。

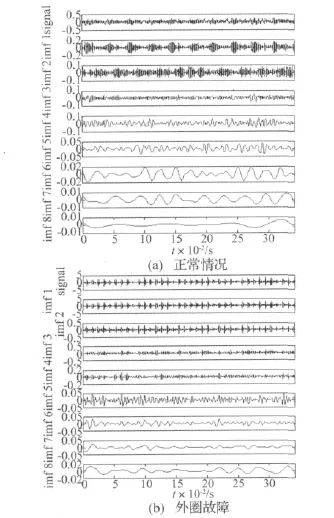
图3 不同轴承故障振动信号的EEMD分解Fig.3 EEMD result of the bearing vibration signal

4 基于EEMD与样本熵的轴承故障诊断方法

当损伤程度为0.533 4 mm，载荷为0，转速为1 797 r/min时，轴承正常情况、内圈故障、滚动体故障、外圈故障的样本熵值如图4所示，从图中可以看到，如果直接用原始信号的样本熵作为特征，无法正确区分内圈故障与外圈故障。EEMD可以将信号分解为一系列内蕴模式分量，轴承在不同运行情况下，内蕴模式分量也不同，采用EEMD分解后IMF的SampEn作为特征比只利用原始信号SampEn的优越之外在于:如果只利用原始信号的SampEn，相当于在1个尺度分析;而进行EEMD分解后，相当于在多个尺度对振动信号进行分析，通过多个尺度，可以得到轴承不同故障的深层次信息，更好地对轴承故障进行分类。

图4 轴承不同状况的SampEn值Fig.4 The SampEn vaule of bearing vibration signal

轴承振动信号经过EEMD分解后，得到一系列表征时间尺度的IMF分量和残余函数res，每个IMF与该层提取前的IMF相比，包含了更低的频率成分。计算与各个 IMF分量相对应的 SampEn值，把得到的SampEn1，SampEn2，…，SampEnn作为轴承故障分类的特征值。其中，最初的几个IMF分量包含了振动信号的最主要的信息。经过对各种故障轴承振动信号EEMD分解结果的观察，选取前 4个 IMF分量的SampEn的值作为特征向量。

支持向量机(Support Vector Machine，SVM)是在统计学习理论基础上发展起来的一种新型机器学习方法，具有泛化能力强、维数不敏感等优点，适于求解高维、小样本、非线性情况下的模式分类和回归分析等问题［15］。

SVM算法最初是为两类分类问题设计的，但轴承故障诊断属于多类模式问题，所以必须扩展(两类)支持向量机来处理多类问题。已经提出多种方法用于多类识别，例如“一对一”，“一对多”等，Hsu and Lin［16］对此做了比较研究，指出“一对一”分类方法在实际应用中优于其它方法。因此，在本文中选用“一对一”的SVM识别方法。

基于EEMD SampEn的轴承故障诊断方法如下:

(1)将原始的轴承振动信号进行EEMD分解，得到内蕴模式分量IMF，取前4个IMF分量进行进一步处理。

(2)利用式(7)计算选取IMF分量的样本熵，参数选取为m=2，r=0.2 Std。

(3)对于训练数据集，用计算得到的4个样本熵作为特征向量，输入SVM进行训练，得到SVM分类器。

(4)把测试样本的IMF分量的SampEn值输入SVM分类器，由SVM分类器的输出得到测试样本的运行状态。

5 实验

为了验证所提方法的有效性，针对CWRU数据进行轴承故障分类实验。数据集的选择参考文献［17-18］的方法，利用载荷为0的10组数据进行9种不同的故障诊断测试，其中包含了不同故障状态的组合，数据集的详细描述如表4所示。数据集中每个样本的采样点数为2 048，共包含了650个样本，其中轴承正常情况的样本数为119个，随机选择其中59个样本作为训练样本集，其余60个样本作为测试样本集;其余每种故障情况的样本数为59个，随机选择其中29个样本作为训练样本集，其余30个样本集作为测试样本集。故障数据集名称中的3组数字分别代表轴承的3种故障状态所对应的故障直径的大小(如对于D070707数据集，代表内圈、滚动体和外圈的故障直径都为0.177 8 mm)，对于 DBALL、DINN 和 DOUT数据集，分别包含了滚动体故障、内圈故障和外圈故障三种故障程度的数据，用于评价对损伤程度的评估能力。

实验中SVM核函数选择最常使用的高斯核函数形式，核函数形式为:

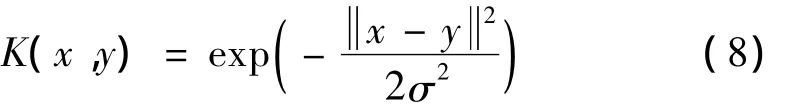
其中，σ为控制核函数高宽的参数。对于线性不可分情况，引入惩罚因子C来控制错误分类。参数取值为σ=1，惩罚因子C=10。

表4 数据集Tab.4 The data set

应用EEMD分解后各IMF的样本熵值作为特征对表4的数据集进行训练与识别，故障分类结果如表5所示。从表中可以看出，在9个故障诊断测试集上只用样本熵值作为特征参数，都取得了比较高的识别率，说明了基于EEMD的样本熵方法用于轴承故障诊断的有效性。

表5 轴承故障分类正确率Tab.5 The recognition rate of bearing fault diagnosis

6 结论

本文提出一种基于EEMD与样本熵的轴承故障诊断方法，利用实测轴承故障振动信号实验表明:

(1)样本熵分析方法只需要较短数据就可得出稳健的估计值，是一种具有较好的抗噪和抗干扰能力的非线性分析方法。通过对轴承正常运行、内圈故障、滚动体故障、外圈故障振动信号分析实验表明，当轴承出现故障时，样本熵的值会有所改变，不同的故障，样本熵的值也不同，说明样本熵作为轴承故障诊断的特征的有效性。

(2)当轴承出现轻微故障(内圈故障、滚动体故障、外圈故障)时，样本熵值会突然变大，随着损伤的进一步扩展，样本熵值会变小，然后又变大。这种特性表明样本熵在轴承早期故障诊断方面有潜在的应用前景。

(3)对轴承振动信号进行EEMD分解后，再进行样本熵特征提取，比直接对轴承振动信号进行样本熵特征提取，可以发现轴承信号中更深层次的信息，得到更好的轴承故障诊断效果。

［1］陶新民，徐 晶，杨立标，等.基于GARCH模型MSVM的轴承故障诊断方法［J］.振动与冲击，2010，29(5):11-15.

［2］郝如江，卢文秀，褚福磊.滚动轴承故障信号的多尺度形态学分析［J］.机械工程学报，2008，44(11):160-165.

［3］王晓冬，何正嘉，訾艳阳.滚动轴承故障诊断的多小波谱峭度方法［J］.西安交通大学学报，2010，44(3):77-81.

［4］李 琳，张永祥，明廷涛.EMD降噪的关联维数在齿轮故障诊断中的应用研究［J］.振动与冲击，2009，28(4):145-148.

［5］王 浩，张来斌，王朝晖，等.迭代奇异值分解降噪与关联维数在烟气轮机故障诊断中的应用［J］.中国石油大学学报:自然科学版，2009，33(1):93-98，108.

［6］Yan，Gao R X.Approximate entropy as a diagnostic tool for machine health monitoring［J］.Mechanical Systems and Signal Processing，2007，21(2):824-839.

［7］ Pincus S M.Approximate entropy as a measure of system complexity［C］.Proc.Natl.Acad.Sci USA，1991，88:2297-2301.

［8］ Lake D E，Richman J S，Griffin M P，et al.Sample entropy analysis of neonatal heart rate variability［J］.Am.J.Physiol Regul.Integr.Comp.Physiol，2002，283(3):789-797.

［9］Pincus S M.Assessing serial irregularity and its implications for health［J］.Ann.N.Y.Acad.Sci，2002，954:245-267.

［10］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hibert Spectrum for nonlinear and nonstationary time series analysis［C］.Proc.R.Soc.Lond.A，1998，454:903-995.

［11］ Wu Z，Huang N E，Ensemble empirical mode decomposition:a noise-assisted data analysis method［R］.Center for Ocean-Land-Atmosphere Studies，2005，Technical Report 193.

［12］ Alcaraz R， Rieta JJ. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms［J］.Biomedical Signal Processing and Control，2010，5(1):1-14.

［13］ http://www.eecs.cwru.edu/laboratory/bearing，Bearing Data Center Website，Case Western Reserve University.

［14］ Huang N E，Shen Z，Long S R.A new view of nonlinear water waves:the Hibert spectrum［J］.Annu.Rev.Fluid Mech.，1999，31:417-457.

［15］Vapnik V N.统计学习理论的本质［M］.北京:清华大学出版社，2000.

［16］Hsu C W，Lin C J.A comparison of methods for multi-class support vector machines［J］.IEEE Transactions on Neural Networks，2002，13:415 – 425.

［17］杨永生，张优云.基于集成支持向量机的滚动轴承故障智能诊断研究［J］.煤矿机械，2010，31(4):243-245.

［18］Yang J Y，Zhang YY，Zhu Y S.Intelligent fault diagnosis of rolling element bearing based on SVMs and fractal dimension［J］.Mechanical Systems and Signal Processing，2007，21(5):2012-2024.