基于改进EMD与有限元的测力轮对组桥方案比较

陈双喜，林建辉，陈建政

(西南交通大学 牵引动力国家重点实验室，成都 610031)

高速列车运行时轮轨间将产生接触振动，甚至存在冲击振动，对车辆和轨道使用寿命影响极大，所以研究轮轨之间的相互作用力十分重要。理论计算难以确定其准确数据，只有通过试验进行测量，才能准确地知道轮轨作用力的真实规律。轮轨力作用在轮轨上，因此测力轮对是当前所有轮轨力测量方法中精度最高、效果最明显的［1］。将应变片按照一定的方案组桥后通过集流环输入到应变仪，经过数据处理后得到实际的轮轨力。1968年瑞士的韦伯(Dr.weber)提出连续测力轮对技术，然后不断发展和完善，先后研制了多种测力轮对。随着高速铁路发展，对测力轮对技术提出了更高的要求，主要体现在获得理想的灵敏度和线性度，并且尽量减少各种干扰。国内外学者对此进行了大量研究，提出了很多改进方法［1，4-7］。目前测力轮对还存在一些缺点:电桥波动、作用位置引起的误差、贴片位置无标准、方程解的不稳定等。设计合理的电桥应当尽量减少电桥波动，具有高的灵敏度。在文献［1］中，对组桥方案进行了深入的理论分析与试验验证，并且提出一种测力轮对最佳组桥方案。本文基于有限元技术和一种改进的经验模态分解方法，对这种最佳电桥和国标GB5595-85电桥输出模拟信号进行分解，提取了电桥输出的各个谐波分量，并且对它们的本征模态进行了分析和比较，取得了较好的效果。

1 改进的EMD算法

经验模式分解(EMD)是美国华裔科学家N.E Huang提出的新的信号时频分析方法。它将信号自适应地分解为多个本征函数及一个余项，从而反映信号的内部特点。由于具有自适应分解特性，对非平稳、非线性信号处理具有较高的效率。然而EMD方法只利用了信号中极值点的信息，局部均值的精度较低，且包络的求取需要两次三次样条插值，计算速度较慢;EMD方法虽然能够有效地分析和处理非平稳信号，但在对非平稳信号进行分解时，在数据的两端会产生发散现象，并且这种发散的结果会逐渐向内“污染”整个数据序列而使所得分解结果严重失真，导致所谓的端点效应问题;Huang等人发现EMD分解混有间断事件的信号时，会发生模态混叠现象。因此，有三个问题需要解决:① 如何进一步提高局部均值的求解精度;② 如何有效地消除因边界不连续而产生的边界效应;③ 如何消除可能出现的本征函数模态混叠现象。

EMD方法中以局部极大值与极小值的包络线的均值代替信号局部均值并不是唯一的求解方法，其他求解方法有［8-9］:自适应时变滤波法(ATVFD)、极值域均值模式分解法(EMMD)、改进的极值域均值模式分解法(IEMMD)等。本文以改进的极值域均值模式分解方法(IEMMD)来提高局部均值的求解精度。其基本步骤如下:

① 求出原始数据x(t)中所有局部极值点组成极值点序列e(ti)，其中i=1，2，3…，k。按照式(1)计算出两相邻极值点间的局部均值序列mi:

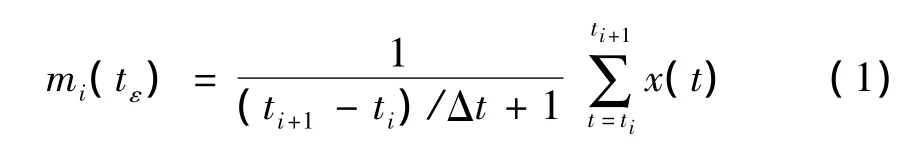
② 假设mi在原始数据x(tii)与x(tii+1)之间(1≤≤k-1)。按式(2)求得mi对应的时间tεi:

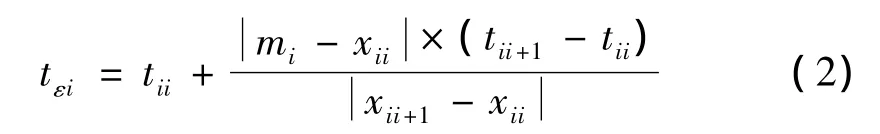
③ 用两个相邻的局部均值mi(tε1)和mi+1(tε2)加权平均求ti+1处极值点的局部均值m(ti+1)，即:

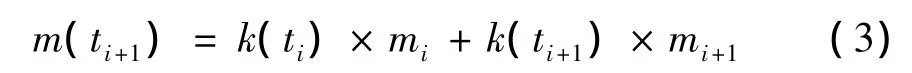
式(3)中的k(ti)和k(ti+1)是通过相似梯形得到的加权系数，即:

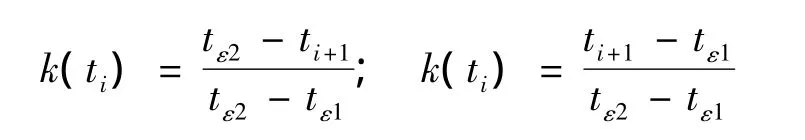
求得极值点处的局部均值之后，就可以用这些点来拟合数据的局部均值曲线，进而分解出IMF。

目前，学者们已经提出了一些抑制端点效应的方法［8-11］:如采用神经网络对数据延拓法、在端点处按照端点数据变化的“平衡位置”附加两条平行线段的方法、极值点延拓法、基于AR模型的时间序列线性预测方法等。边界波形匹配预测法能最大限度地维护原始信号在端部的变化趋势，相对于其它方法而言，其构造的虚拟极值点更加合理，对端点效应的抑制效果更加理想。考虑到计算的精度与成本和适应性，本文以边界波形匹配预测法来抑制端点效应，其基本步骤可见文献［12］。

对于模态混叠问题，Huang提出筛选预设尺寸上限的办法抑制，但没有给出详细的处理方法。许多学者提出一些方法［14-15］:如基于多分辨分析的经验模态分析方法(MEMD)、基于差分与累加求和的分解法等。本文在改进的极值域均值模式分解方法(IEMMD)基础上，结合差分与累加求和法抑制可能出现的模态混叠现象，其详细步骤可见文献［14］。

2 轮轨力测量方法

轮轨接触力包括法向力、蠕滑力、蠕滑力矩，将其从接触斑坐标系分解到轮对坐标系，便得到轮对的横向力、垂向力、纵向力，如图1所示。横向力使辐板轴向受剪切同时产生较大弯曲应变。垂向力主要对辐板产生压应变和一个弯矩，弯矩的大小与作用点的位置有关系。

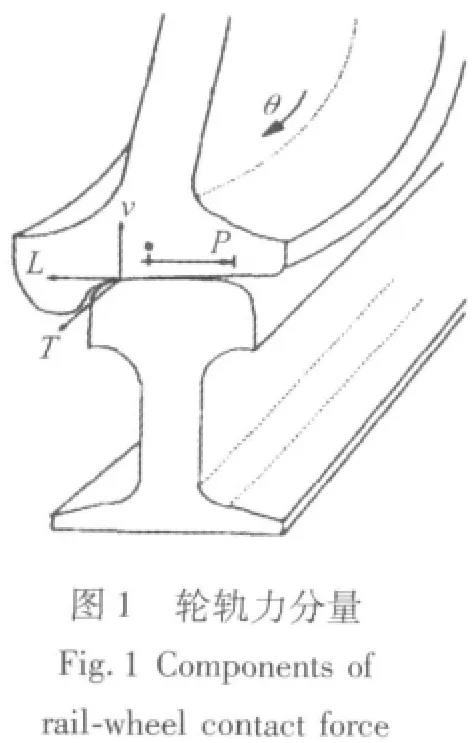
在恒定载荷作用下，轮辐板弹性应变ε是车轮转动角度θ的周期函数。所谓的连续测量原理:当轮轨力不变时，测量电桥的输出不随轮对的转角变化而变化，也就是说，测量轮轨力电桥的输出始终与轮轨力的瞬时值成正比，而与转角无关。为了实现连续测量，需要多个输出波形相同，有一定相位差的电桥组合起来。在实际运用中，考虑到各种干扰因素，应变片一般组成惠斯登全桥，如图2所示。电桥输出与电压成正比，相对桥臂的应变相加，相邻桥臂的应变相减，如式(4)所示(式(4)中K、E为常数)。同时由式(4)可知，将相邻臂上的应变片布置在轮对辐板同一半径上可以抵消离心力和温度应力(轴对称应力)的影响。

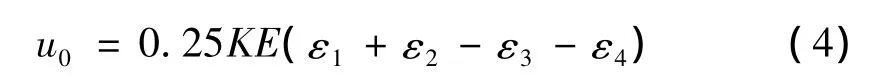
2.1 两种组桥方案

从数学角度而言，轮辐板上某点旋转θ°后的应变等于同一半径下与该点间隔θ°点的应变，也就是说，某点在恒定载荷下的应变时间分布等效于某一瞬间同一半径下应变沿圆周方向的空间分布。各种组桥方案原理上都是利用三角函数的特性，通过不同频率下谐波函数的组合，构造特殊的周期函数，从而消除谐波分量，实现连续测量。测力轮对测量电桥由多个轴对称的应变片组成，单个电桥的输出［1］为:

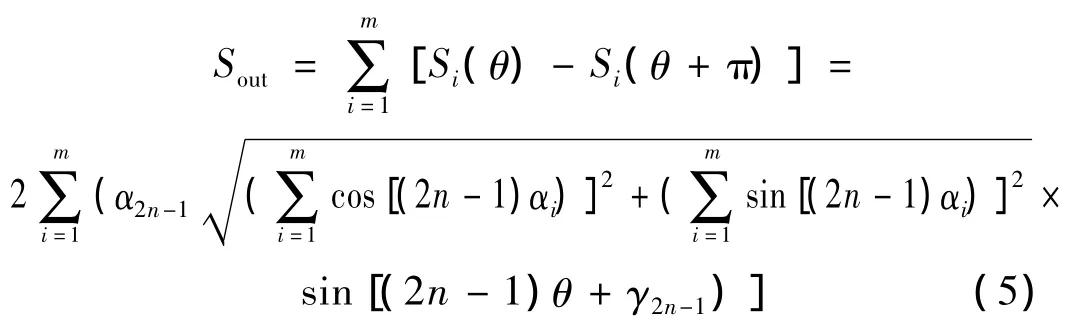
式中，Si为各对称分量的输出，m为对称分量的数目，n为谐波分量的次数，αi为各个对称分量的初始相位，γ2n-1为电桥初始相位。

电桥输出只包含奇数次谐波分量，不包括偶次谐波分量，各个奇数次谐波分量的幅值为:

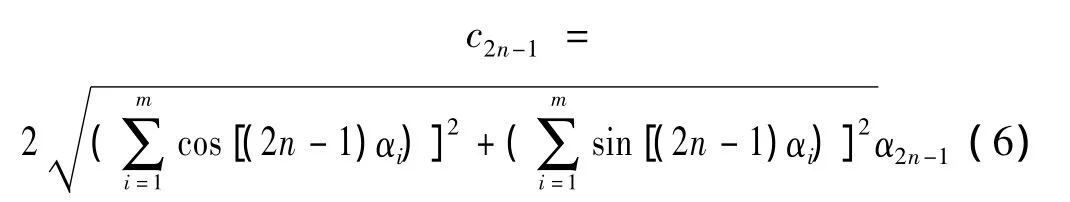
欲消除某次谐波，只需令式(6)中的αi=0。文献［1］对组桥方案进行了深入地研究，其计算结果表明，两个对称分量组桥和三个对称分量均无法同时消除输出电桥的三次、五次谐波。同时对四个对称分量组桥进行推导，得出了理论上能消除三次、五次谐波干扰的最佳组桥方案，其电桥如图3所示，上图为最佳组桥电桥，下图为国标GB5595-85电桥。两者均由四个对称分量组成。区别在于各个对称分量的布置位置有所差异。

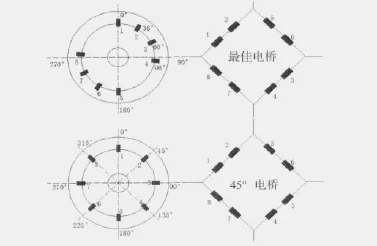
图3 两种不同的电桥组桥方案Fig.3 Two different kinds of electrical bridge

最佳组桥的相位差与谐波幅值如表1所示。

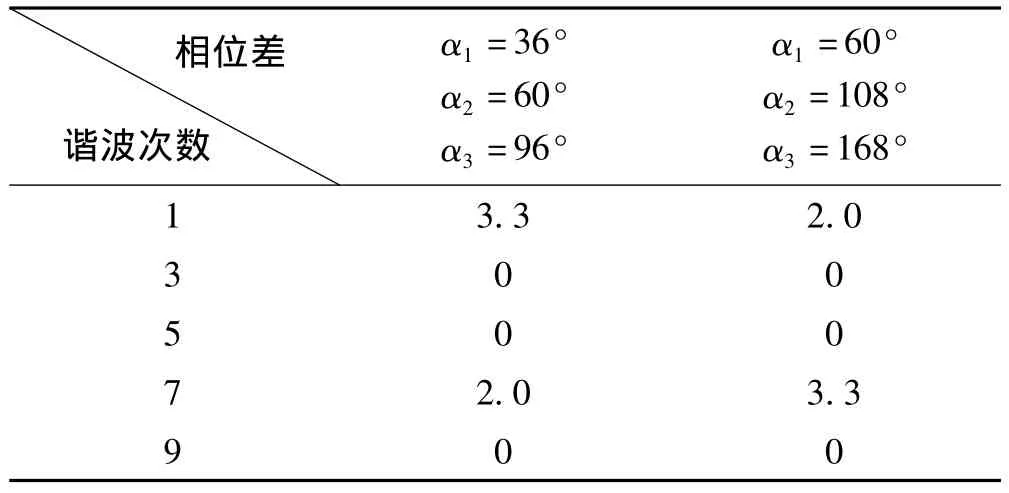
表1 最佳组桥方案相位与谐波幅值Tab.1 Phase and harmonic amplitude of the best bridge

本文基于有限元方法、现代信号处理技术对上述两种电桥进行研究比较。一方面验证组桥理论研究的正确性，另一方面比较两种电桥的优缺点。

2.2 有限元技术在测力轮对中应用

有限元技术已成功应用于测力轮对的设计和标定，极大地提高了效率。通过力学分析能够详细掌握轮对辐板面应变分布情况，模拟不同组桥的电桥输出。而研究静态和动态情况下的轮对轮辐板面的应变是寻求最佳贴片位置，建立组桥方案，提高测量精度的基础。

本文以高速动车组CRH2的直幅板轮对为例，建立三维有限元模型，进行模拟加载与分析。为了保证计算精度，对车轮和车轴都进行六面体网格划分。对于车轮踏面，将进行网格细分。轮对有限元模型如图4所示。

图4 轮对有限元模型Fig.4 FE model of instrumented wheel-set

假设踏面轮轨为单点接触，载荷点沿着接触线上各个节点横向移动模拟作用点位置变化(以滚动圆为坐标零点，在-54 mm～60 mm范围内变化)。静力学分析设置多个载荷步分部加载，每个载荷步间隔1～10 mm;踏面上各个节点分别施加横向力、垂向力各1 t单位载荷。

通过有限元模拟计算得到大量数据。静态分析结果与文献［1-5］一致，最佳作用点位置确定参考了文献［1-5，7］，仿真得到了分别对横向力、垂向力和作用点位置电桥敏感的三个半径:R=157 mm、R=290 mm、R=328 mm。提取各个半径下周向节点的径向弹性应变数据，根据文献［1］计算出电桥的模拟输出。

3 两种组桥方案的电桥输出与比较

3.1 两种电桥输出信号比较

图5所示为前述两种组桥方案横向力测量电桥的模拟输出及其精度比较，可见最佳电桥的波动幅值远远小于GB5595-85电桥，其测量精度大于GB5595-85电桥:GB5595-85电桥输出波动明显偏大，大于2个单位微应变;而最佳组桥方案的电桥输出波动小于0.5个单位微应变。如前述，这是由于最佳组桥方案从理论上消除了幅值较大的三次、五次谐波对电桥波动的影响。可见，有限元模拟输出结果与理论计算结果一致。

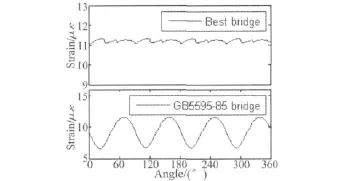
图5 两种组桥方案电桥输出Fig.5 Output of two electrical bridges

3.2 GB5595－85电桥输出信号与分析

GB5595-85电桥由两个间隔90°的单桥(如图3所示)组成。运用前述的改进EMD方法对上述电桥输出进行分解，计算结果如图6所示，左边为时域信号，右边为对应频谱。在第一步即分解出信号的最高谐波分量c1(4次谐波)。可见，GB5595-85电桥输出成分主要是幅值较大的4次谐波(还存在微弱的8次谐波)。还可见，前述的改进EMD方法有效地抑制了端点效应，具有更高的精度。对于这种波形较短的电桥模拟输出，抑制端点效应和更高的局部均值求解就具有了更重要的意义。

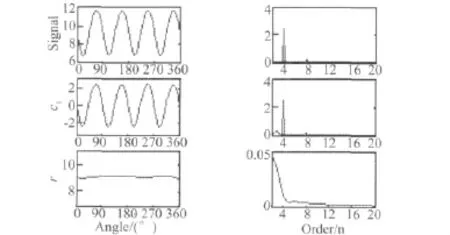
图6 GB5595-85电桥输出与改进EMD分解Fig.6 Improved EMD decomposition of output signal of GB5595-85 bridge

目前大部分垂向力、横向力电桥都采用平方和相加或者绝对值叠加的方法消除谐波的影响。对于两个间隔90°的4对称分量组桥方案，本文采取平方和相加的方法，即电桥的输出函数为:

式(7)中，a1、a3、a5、a7、a9为单桥输出各次谐波的系数。

从式(7)可知，对于两个间隔90°的4对称分量组桥方案，其电桥输出包含4、8、12、16次谐波分量。由于GB5595-85电桥输出的谐波系数a7、a9为零，因此输出仅有4、8次谐波，这与图6的模拟输出一致。可见，模拟输出和理论计算一致，此种电桥输出成分主要是幅值较大的4次谐波。

3.3 最佳电桥的信号输出与分析

最佳组桥方案同样由两个间隔90°的单桥(如图2所示)组成。运用前述的改进EMD方法对上述电桥输出进行分解，对于存在明显模态混叠的本征函数运用前述方法重新分解，分解结果如图7所示，左边位时域信号，右边为对应频谱。

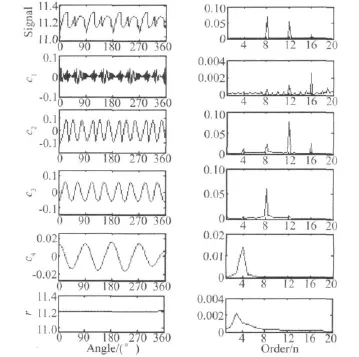
图7 最佳电桥输出与改进EMD分解Fig.7 Improved EMD decomposition of output signal of the best bridge

如图7所示，最佳电桥输出成分比较复杂，高频分量较多，存在4次、8次、12次、16次谐波分量。其中8次、12次谐波分量处于同一数量级，16次谐波分量次之，4次谐波分量所占能量最小。可见，此种组桥方案电桥输出信号成分比GB5595-85电桥复杂，虽然存在更多的高频分量，但其信号幅值波动远小于GB5595-85电桥。

目前的低速测力轮对技术，采样截止频率100 Hz以内，低通滤波频率20 Hz以内。而对于高速测力轮对，其采样频率至少在1 000 Hz以上，其滤波频率也更高。表2给出了不同速度下，各次数谐波分量对应的频率。由表2可知，对于速度350 km/h的高速测力轮对，若低通滤波频率大于143.9 Hz，则4次谐波分量无法滤除;若低通滤波频率大于287.9 Hz，则8次谐波分量无法滤除;若低通滤波频率大于431.8 Hz，则12次谐波分量无法滤除。在此情况下，通过前述的分析可知，最佳电桥的电桥输出波动会远小于GB5595-85，因而具有更高的精度。

表2 不同速度下的谐波频率(Hz)Tab.2 The harmonic frequency under different velocity

4 结论

(1)有限元模拟结果与理论计算结果一致，说明了有限元方法在电桥仿真中的正确性。

(2)基于改进的极值域均值模式分解方法(IEMMD)，可以自适应地将信号分解成本征模态;边界波形匹配预测法成功抑制了端点效应;结合差分与累加求和法抑制了出现的模态混叠现象，分离出高次谐波。

(3)传统GB5595-85电桥波动较大，主要是由于存在幅值较大的低次谐波分量;最佳组桥方案电桥输出高次谐波分量较为复杂，但由于消除了幅值较大的低次谐波分量，能有效降低电桥波动。

［1］陈建政.轮轨作用力和接触点在线测量理论研究［D］.成都:西南交通大学，2008.

［2］ Gullers P，Andersson L，Lundén R.High-frequency wheelrail contactforces-field measurementsand influence of corrugation［C］//Proceedings of the Seventh International Conference on Contact Mechanics and Wear of Rail/Wheel Systems，Brisbane，Australia，2008，265，1472-1478.

［3］Nielsen J C O.High-frequency vertical wheel-rail contact forces-validation of aprediction model by field testing［C］//Proceedings of the 7th International Conference on Contact Mechanics and Wear of Rail/Wheel Systems， Brisbane，Australia，24-27 September，2006:41-48.

［4］张利民，金学松.基于测力轮对的轮轨瞬态作用力仿真［J］.铁道学报，1998 ，20(增刊):146-151.

［5］常崇义，王成国，李 兰，等.连续测力轮对的数字试验研究［J］.铁道机车车辆，2007，27(5):3-5.

［6］刘尚举，金学松，张立民.提高测力轮对测量精度的研究［J］.铁道车辆，1998，36(2):32-34.

［7］陈建政，林建辉.在线连续测量轮轨接触点的神经网络方法［J］.振动与冲击，2007，26(5):90-92.

［8］余 泊.自适应时频分析方法及其在故障诊断中的应用［D］.大连:大连理工大学，1998.

［9］盖 强.局域波时频分析方法的理论研究与应用［D］.大连:大连理工大学，2001.

［10］ Zhao J P，Huang D J.Mirror extending and circular spline function for empirical mode decomposition method ［J］.Journal of Zhejiang University，2001，2(3):247-252.

［11］邓拥军.EMD方法及Hilbert变换中便捷问题的处理［J］.科学通报，2001，46(3):257-263.

［12］邵晨曦，王 剑，范金锋，等.一种自适应的EMD端点延拓方法［J］.电子学报，2007，35(10):1944-1946.

［13］沈 路，杨富春，周晓军，等.基于改进EMD与形态滤波的齿轮故障特征提取［J］.振动与冲击，2010，29(3):154-157.

［14］高云超，桑恩方，许继友.分离EMD中混叠模态的新方法［J］.哈尔滨工程大学学报，2008，29(9):963-966.

［15］鞠萍华，秦树人，秦 毅，等.多分辨EMD方法与频域平均在齿轮早期故障诊断中的研究［J］.振动与冲击，2009，28(5):97-100.